Cálculo I

Cálculo I
Humberto José Bortolossi
Departamento de Matemática Aplicada
Universidade Federal Fluminense
Aula 17
15 de maio de 2008
Aula 17
Cálculo I
1
O teorema de Rolle e o teorema do
valor médio
Aula 17
Cálculo I
2
O teorema de Rolle
Teorema
Seja f uma função derivável em (a, b) e contínua em [a, b]. Se
f (a) = f (b) = 0, então existe pelo menos um ponto c ∈ (a, b)
tal que f 0 (c) = 0.
Aula 17
Cálculo I
3
Exemplo
Se r > 0 e n é um inteiro não-negativo qualquer, prove que
f (x) = x 2 n+1 + r x + s não pode ter duas raízes reais distintas.
Solução. Suponha, por absurdo, que y = f (x) tenha duas raízes reais
distintas a e b. Assim, f (a) = f (b) = 0. Como f é diferenciável em (a, b)
e contínua em [a, b], segue-se pelo teorema de Rolle que existe pelo menos
um c ∈ (a, b) tal que
f 0 (c) = 0,
isto é, f 0 (x) = (2 n + 1) x 2 n + r possui pelo menos uma raiz real em (a, b).
Mas isto é uma contradição, pois para todo x ∈ R, ocorre que
(2 n + 1) x 2 n + r > 0.
| {z } |{z} |{z}
>0
≥0
>0
Isto mostra que f (x) = x 2 n+1 +r x +s não pode ter duas raízes reais distintas.
Aula 17
Cálculo I
4
Exemplo
Se r > 0 e n é um inteiro não-negativo qualquer, prove que
f (x) = x 2 n+1 + r x + s não pode ter duas raízes reais distintas.
Solução. Suponha, por absurdo, que y = f (x) tenha duas raízes reais
distintas a e b. Assim, f (a) = f (b) = 0. Como f é diferenciável em (a, b)
e contínua em [a, b], segue-se pelo teorema de Rolle que existe pelo menos
um c ∈ (a, b) tal que
f 0 (c) = 0,
isto é, f 0 (x) = (2 n + 1) x 2 n + r possui pelo menos uma raiz real em (a, b).
Mas isto é uma contradição, pois para todo x ∈ R, ocorre que
(2 n + 1) x 2 n + r > 0.
| {z } |{z} |{z}
>0
≥0
>0
Isto mostra que f (x) = x 2 n+1 +r x +s não pode ter duas raízes reais distintas.
Aula 17
Cálculo I
5
Exemplo
Se r > 0 e n é um inteiro não-negativo qualquer, prove que
f (x) = x 2 n+1 + r x + s não pode ter duas raízes reais distintas.
Solução. Suponha, por absurdo, que y = f (x) tenha duas raízes reais
distintas a e b. Assim, f (a) = f (b) = 0. Como f é diferenciável em (a, b)
e contínua em [a, b], segue-se pelo teorema de Rolle que existe pelo menos
um c ∈ (a, b) tal que
f 0 (c) = 0,
isto é, f 0 (x) = (2 n + 1) x 2 n + r possui pelo menos uma raiz real em (a, b).
Mas isto é uma contradição, pois para todo x ∈ R, ocorre que
(2 n + 1) x 2 n + r > 0.
| {z } |{z} |{z}
>0
≥0
>0
Isto mostra que f (x) = x 2 n+1 +r x +s não pode ter duas raízes reais distintas.
Aula 17
Cálculo I
6
Exemplo
Se r > 0 e n é um inteiro não-negativo qualquer, prove que
f (x) = x 2 n+1 + r x + s não pode ter duas raízes reais distintas.
Solução. Suponha, por absurdo, que y = f (x) tenha duas raízes reais
distintas a e b. Assim, f (a) = f (b) = 0. Como f é diferenciável em (a, b)
e contínua em [a, b], segue-se pelo teorema de Rolle que existe pelo menos
um c ∈ (a, b) tal que
f 0 (c) = 0,
isto é, f 0 (x) = (2 n + 1) x 2 n + r possui pelo menos uma raiz real em (a, b).
Mas isto é uma contradição, pois para todo x ∈ R, ocorre que
(2 n + 1) x 2 n + r > 0.
| {z } |{z} |{z}
>0
≥0
>0
Isto mostra que f (x) = x 2 n+1 +r x +s não pode ter duas raízes reais distintas.
Aula 17
Cálculo I
7
Exemplo
Se r > 0 e n é um inteiro não-negativo qualquer, prove que
f (x) = x 2 n+1 + r x + s não pode ter duas raízes reais distintas.
Solução. Suponha, por absurdo, que y = f (x) tenha duas raízes reais
distintas a e b. Assim, f (a) = f (b) = 0. Como f é diferenciável em (a, b)
e contínua em [a, b], segue-se pelo teorema de Rolle que existe pelo menos
um c ∈ (a, b) tal que
f 0 (c) = 0,
isto é, f 0 (x) = (2 n + 1) x 2 n + r possui pelo menos uma raiz real em (a, b).
Mas isto é uma contradição, pois para todo x ∈ R, ocorre que
(2 n + 1) x 2 n + r > 0.
| {z } |{z} |{z}
>0
≥0
>0
Isto mostra que f (x) = x 2 n+1 +r x +s não pode ter duas raízes reais distintas.
Aula 17
Cálculo I
8
Exemplo
Se r > 0 e n é um inteiro não-negativo qualquer, prove que
f (x) = x 2 n+1 + r x + s não pode ter duas raízes reais distintas.
Solução. Suponha, por absurdo, que y = f (x) tenha duas raízes reais
distintas a e b. Assim, f (a) = f (b) = 0. Como f é diferenciável em (a, b)
e contínua em [a, b], segue-se pelo teorema de Rolle que existe pelo menos
um c ∈ (a, b) tal que
f 0 (c) = 0,
isto é, f 0 (x) = (2 n + 1) x 2 n + r possui pelo menos uma raiz real em (a, b).
Mas isto é uma contradição, pois para todo x ∈ R, ocorre que
(2 n + 1) x 2 n + r > 0.
| {z } |{z} |{z}
>0
≥0
>0
Isto mostra que f (x) = x 2 n+1 +r x +s não pode ter duas raízes reais distintas.
Aula 17
Cálculo I
9
Exemplo
Se r > 0 e n é um inteiro não-negativo qualquer, prove que
f (x) = x 2 n+1 + r x + s não pode ter duas raízes reais distintas.
Solução. Suponha, por absurdo, que y = f (x) tenha duas raízes reais
distintas a e b. Assim, f (a) = f (b) = 0. Como f é diferenciável em (a, b)
e contínua em [a, b], segue-se pelo teorema de Rolle que existe pelo menos
um c ∈ (a, b) tal que
f 0 (c) = 0,
isto é, f 0 (x) = (2 n + 1) x 2 n + r possui pelo menos uma raiz real em (a, b).
Mas isto é uma contradição, pois para todo x ∈ R, ocorre que
(2 n + 1) x 2 n + r > 0.
| {z } |{z} |{z}
>0
≥0
>0
Isto mostra que f (x) = x 2 n+1 +r x +s não pode ter duas raízes reais distintas.
Aula 17
Cálculo I
10
Exemplo
Se r > 0 e n é um inteiro não-negativo qualquer, prove que
f (x) = x 2 n+1 + r x + s não pode ter duas raízes reais distintas.
Solução. Suponha, por absurdo, que y = f (x) tenha duas raízes reais
distintas a e b. Assim, f (a) = f (b) = 0. Como f é diferenciável em (a, b)
e contínua em [a, b], segue-se pelo teorema de Rolle que existe pelo menos
um c ∈ (a, b) tal que
f 0 (c) = 0,
isto é, f 0 (x) = (2 n + 1) x 2 n + r possui pelo menos uma raiz real em (a, b).
Mas isto é uma contradição, pois para todo x ∈ R, ocorre que
(2 n + 1) x 2 n + r > 0.
| {z } |{z} |{z}
>0
≥0
>0
Isto mostra que f (x) = x 2 n+1 +r x +s não pode ter duas raízes reais distintas.
Aula 17
Cálculo I
11
O teorema do valor médio
Teorema
Se f é uma função derivável em (a, b) e contínua em [a, b], então existe pelo menos um
ponto c ∈ (a, b) tal que
f (b) − f (a)
= f 0 (c).
b−a
Aula 17
Cálculo I
12
O teorema do valor médio
Teorema
Se f é uma função derivável em (a, b) e contínua em [a, b], então existe pelo menos um
ponto c ∈ (a, b) tal que
f (b) − f (a)
= f 0 (c).
b−a
Aula 17
Cálculo I
13
O teorema do valor médio
Teorema
Se f é uma função derivável em (a, b) e contínua em [a, b], então existe pelo menos um
ponto c ∈ (a, b) tal que
f (b) − f (a)
= f 0 (c).
b−a
Aula 17
Cálculo I
14
O teorema do valor médio
Teorema
Se f é uma função derivável em (a, b) e contínua em [a, b], então existe pelo menos um
ponto c ∈ (a, b) tal que
f (b) − f (a)
= f 0 (c).
b−a
Aula 17
Cálculo I
15
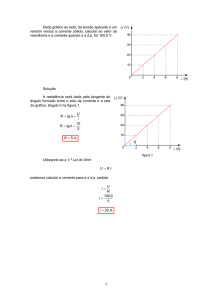
Exemplo
Seja f : [−1, 2] → R contínua em [−1, 2], diferenciável em (−1, 2) com
f (−1) = −1 e f (2) = 5. Prove que existe um ponto do gráfico de f em
que a reta tangente é paralela à reta y = 2 x.
Solução. Pelo teorema do valor médio, existe c ∈ (−1, 2) tal que
f 0 (c) =
f (2) − f (−1)
5 − (−1)
6
=
= = 2.
2 − (−1)
2 − (−1)
3
Assim, a reta tangente ao gráfico de f no ponto (c, f (c)) tem coeficiente
angular igual a 2 sendo, portanto, paralela à reta y = 2 x.
Aula 17
Cálculo I
16
Exemplo
Seja f : [−1, 2] → R contínua em [−1, 2], diferenciável em (−1, 2) com
f (−1) = −1 e f (2) = 5. Prove que existe um ponto do gráfico de f em
que a reta tangente é paralela à reta y = 2 x.
Solução. Pelo teorema do valor médio, existe c ∈ (−1, 2) tal que
f 0 (c) =
f (2) − f (−1)
5 − (−1)
6
=
= = 2.
2 − (−1)
2 − (−1)
3
Assim, a reta tangente ao gráfico de f no ponto (c, f (c)) tem coeficiente
angular igual a 2 sendo, portanto, paralela à reta y = 2 x.
Aula 17
Cálculo I
17
Exemplo
Seja f : [−1, 2] → R contínua em [−1, 2], diferenciável em (−1, 2) com
f (−1) = −1 e f (2) = 5. Prove que existe um ponto do gráfico de f em
que a reta tangente é paralela à reta y = 2 x.
Solução. Pelo teorema do valor médio, existe c ∈ (−1, 2) tal que
f 0 (c) =
f (2) − f (−1)
5 − (−1)
6
=
= = 2.
2 − (−1)
2 − (−1)
3
Assim, a reta tangente ao gráfico de f no ponto (c, f (c)) tem coeficiente
angular igual a 2 sendo, portanto, paralela à reta y = 2 x.
Aula 17
Cálculo I
18
Exemplo
Seja f : [−1, 2] → R contínua em [−1, 2], diferenciável em (−1, 2) com
f (−1) = −1 e f (2) = 5. Prove que existe um ponto do gráfico de f em
que a reta tangente é paralela à reta y = 2 x.
Solução. Pelo teorema do valor médio, existe c ∈ (−1, 2) tal que
f 0 (c) =
f (2) − f (−1)
5 − (−1)
6
=
= = 2.
2 − (−1)
2 − (−1)
3
Assim, a reta tangente ao gráfico de f no ponto (c, f (c)) tem coeficiente
angular igual a 2 sendo, portanto, paralela à reta y = 2 x.
Aula 17
Cálculo I
19
Exemplo
Seja f : [−1, 2] → R contínua em [−1, 2], diferenciável em (−1, 2) com
f (−1) = −1 e f (2) = 5. Prove que existe um ponto do gráfico de f em
que a reta tangente é paralela à reta y = 2 x.
Solução. Pelo teorema do valor médio, existe c ∈ (−1, 2) tal que
f 0 (c) =
f (2) − f (−1)
5 − (−1)
6
=
= = 2.
2 − (−1)
2 − (−1)
3
Assim, a reta tangente ao gráfico de f no ponto (c, f (c)) tem coeficiente
angular igual a 2 sendo, portanto, paralela à reta y = 2 x.
Aula 17
Cálculo I
20
Exemplo
Seja f : [−1, 2] → R contínua em [−1, 2], diferenciável em (−1, 2) com
f (−1) = −1 e f (2) = 5. Prove que existe um ponto do gráfico de f em
que a reta tangente é paralela à reta y = 2 x.
Solução. Pelo teorema do valor médio, existe c ∈ (−1, 2) tal que
f 0 (c) =
f (2) − f (−1)
5 − (−1)
6
=
= = 2.
2 − (−1)
2 − (−1)
3
Assim, a reta tangente ao gráfico de f no ponto (c, f (c)) tem coeficiente
angular igual a 2 sendo, portanto, paralela à reta y = 2 x.
Aula 17
Cálculo I
21