CARACTERIZAÇÃO DE FERROELETRETOS POR PONTES AUTOBALANCEADAS
287
CARACTERIZAÇÃO DE FERROELETRETOS
POR PONTES AUTOBALANCEADAS
Heitor Cury Basso
Departamento de Engenharia Elétrica,
EESC-USP, São Carlos, SP
Resumo
A área de materiais compostos com coeficientes piezelétricos altos, denominados ferroeletretos, está em franco
desenvolvimento, com uma série de resultados interessantes. Porém, esses materiais apresentam novos desafios na
preparação e caracterização elétrica. Na caracterização, vários grupos de pesquisa têm utilizado a ponte autobalanceada,
um equipamento automático para medida de impedância elétrica em amplas faixas de frequência. Contudo, por suas
características não-lineares intrínsecas, os ferroeletretos não são quantitativamente analisados por tais equipamentos,
e os resultado obtidos estão ligados a imperfeições dos mesmos.
Palavras-chave: ferroeletretos, ponte autobalanceada, caracterização de impedância.
Introdução
Eletretos são estudados há mais de um século (Sessler,
1987) e decorrem do carregamento de materiais altamente
isolantes que, por isso, conseguem manter as cargas injetadas,
dipolos induzidos ou alinhados por longo tempo, sendo
que em alguns materiais o tempo de decaimento desse
carregamento é estimado em século. Essa característica
é utilizada, por exemplo, em transdutores piezelétricos
tais como os microfones de eletreto, amplamente utilizados
em equipamentos eletrônicos pela robustez e baixo custo
apresentados.
Nos últimos dez anos, uma nova abordagem aos
eletretos vem se desenvolvendo, em que a utilização de
compósitos ou a alteração das propriedades mecânicas
de polímeros tem aumentado significativamente o leque
de aplicação dessa característica de dielétricos. A primeira
grande alteração surge com o desenvolvimento de espumas
de polipropileno (PP) (Gerhard-Multhaupt, 2002). O PP
é um bom eletreto à temperatura ambiente, mas na forma
de espuma apresenta baixo módulo de elasticidade, o que
aumenta a resposta piezelétrica, sendo esta dada por:
C pe =
∂Q ∂P 1 ∂x ∂P 1
=
=
∂F ∂x d 0 ∂p ∂x E
(1)
em que Cpe é o coeficiente piezelétrico ou a razão entre a
carga gerada pelo elemento e a força de compressão (tração)
aplicada neste, P é a densidade de momento de dipolo
criada pela alteração dx na espessura do material, d0 é a
espessura do material, p a pressão e E o módulo de
elasticidade. Como a espuma de PP apresenta um módulo
de elasticidade cerca de cem vezes menor que o material
compacto, a resposta é correspondentemente cerca de cem
vezes maior.
Um avanço subsequente foi a criação de estruturas
com filmes de fluoretilenopropileno (FEP) (Altafim et
al., 2006), material que, se utilizado como eletreto,
apresenta uma faixa de temperatura de trabalho maior
que o PP, já que este perde suas propriedades acima
de 70ºC. A primeira estrutura proposta envolvia dois
filmes de FEP soldados termicamente, mas um desenvolvimento posterior apresentou uma estrutura com três
filmes (Basso et al., 2007), o que possibilita sua produção
em escala industrial. Essas novas estruturas, bem como
as espumas de polímeros, passaram a ser denominadas
ferroeletretos.
A caracterização desses materiais geralmente
envolve a medida do coeficiente piezelétrico, pela
aplicação de força periódica no material e medida da
carga elétrica produzida. Tais medidas só são possíveis
em baixas frequências, em que, porém, a relação sinalruído elétrico não é muito favorável. Outra possibilidade
é a medida do efeito inverso, em que uma tensão elétrica
causa uma variação na carga do ferroeletreto e com isso
uma força, que gera deformação no material. Essa
caracterização pode ser feita em altas frequências, porém
a determinação direta da deformação é um grande
problema. Outra possibilidade envolve a medida da
potência acústica gerada, com a desvantagem de complicar
a análise dos resultados.
Outra sistemática de caracterização que tem sido
empregada por alguns grupos de pesquisa (Mellinger,
2003, e referências ai citadas) é a medida de impedância
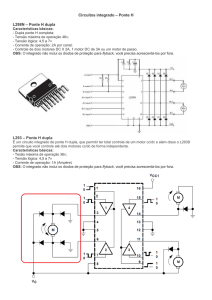
dos ferroeletretos com ponte autobalanceada. Um resultado
típico desse tipo de medida está na Figura 1, em que C’e
C” correspondem, respectivamente, à parte real e imaginária
da capacitância total medida do ferroeletreto.
Minerva, 6(3): 287-292
95,05p
0
95,00p
–50f
94,95p
–100f
94,90p
–150f
94,85p
–200f
94,80p
–250f
–300f
600k
94,75p
0
100k
200k
300k
400k
C" (F)
BASSO
C' (F)
288
500k
w (rad/s)
Figura 1
equipamento apresenta distorções harmônicas na
excitação, ou seja, a ponte autobalanceada não é o
equipamento adequado para caracterizar quantitativamente
ferroeletretos, exceto em algumas características mecânicas
dinâmicas.
Por ser uma técnica altamente difundida de medida
de componentes passivos lineares, há no mercado diversos
equipamentos automáticos que determinam a impedância
de um componente em uma faixa ampla de frequência
(pelo menos entre 20 Hz e alguns MHz) com alta precisão.
Esse equipamento também pode ser empregado para
medidas de espectroscopia dielétrica, em que a permissividade elétrica complexa de um material dielétrico
ε ' r + jε "r é medida em função da frequência. Para tanto
basta construir um capacitor com esse dielétrico e medilo na ponte.
Neste trabalho serão apresentadas as equações
básicas da corrente elétrica de resposta de um ferroeletreto
a uma tensão externa alternada a partir de um modelo
macroscópico, e será mostrado que, em virtude do caráter
não-linear dessa resposta, a caracterização de ferroeletretos
por ponte autobalanceada só é possível quando esse
Modelo do Ferroeletreto
A estrutura básica de um ferroeletreto modelo,
baseado na estrutura apresentada por Basso et al., é
apresentada na Figura 2. O sistema é composto por dois
filmes de polímero dielétrico idênticos, com permissividade
elétrica relativa εr e espessura t, separados por outro filme
dielétrico de tal modo que se forma uma cavidade preenchida
com um gás, sendo d a espessura da cavidade e σ1 e σ2
as densidades superficiais de carga na cavidade e nos
eletrodos externos, respectivamente (representados pelos
traços escuros).
VP
t
?r
- - - +
+
+
- - - +
+
+
- - - - +
+
+
??
- - - - +
+
Figura 2
Minerva, 6(3): 287-292
+
?2
-
+
+
+
d
CARACTERIZAÇÃO DE FERROELETRETOS POR PONTES AUTOBALANCEADAS
289
O processo de produção do ferroeletreto envolve
a aplicação de uma tensão contínua (VP), denominada tensão
de polarização, e negativa no caso representado, alta o
suficiente para ocasionar o acúmulo de cargas nas superfícies
internas dos filmes poliméricos pela quebra dielétrica do
gás, gerando assim s1, cujo valor não será mais alterado,
e caracterizando o carregamento do ferroeletreto Quando
essa tensão é retirada, após o carregamento, surge uma
densidade de carga nos eletrodos externos tal que a tensão
no eletrodo superior vá a zero.
Nesta situação, a relação entre as densidades de carga
interna e externa é dada por:
em que ε0 é a permissividade elétrica do vácuo, pode-se
determinar o valor total da densidade superficial de cargas
nos eletrodos externos.
Para o filme superior resulta –σ2eq+δσ2, já que a
densidade de equilíbrio tem sinal oposto ao da induzida
por V. Assumindo que V <<Vp, a variação da força de
atração será linear com V e pequena em relação à de
equilíbrio, resultando das equações 2, 3 e 4:
⎞
⎛ 2t
σ 1d = σ 2eq ⎜⎜ + d ⎟⎟
ε
⎠
⎝ r
H
2t (ε r + 1) + dε r (ε r − 1)
Vxˆ
δF (V ) = − Aσ 1
(2t + dε r )2
δσ 2 = ε 0
(2)
em que σ 2eq é a densidade de carga de equilíbrio nos
eletrodos. Esse carregamento cria também uma força
eletrostática de atração entre os filmes, cujo módulo é
dado por:
F0 =
A
ε0
(
⎛⎛
⎞
⎜ ⎜ σ 1 − 1 σ 2eq ⎟ σ 1 − σ 2eq
⎟
⎜⎜
εr
⎠
⎝⎝
)⎞⎟⎟
em que A é a área superficial da câmara e que será
compensada pela deformação dos filmes e compressão
do gás dentro da câmara, resultando, para a separação
entre os filmes, no valor de d.
A situação de equilíbrio apresentada acima pode
ser perturbada pela aplicação de uma tensão elétrica por
um gerador externo que, alterando a densidade de carga
nos eletrodos, alterará a força de atração entre os filmes.
Analisando o filme superior, conforme apresentado na
Figura 3, em que I é a corrente de carregamento do sistema
I=A
dσ 2
, e sabendo que a variação na densidade
dt
superficial de carga dos eletrodos externos em função da
tensão aplicada V será dada por:
~V0
(4)
(5)
Note-se que esse resultado indica que a força de
atração total aumenta com a aplicação de uma tensão
positiva, já que δF tem o mesmo sentido que F0.
A variação da força de atração altera a distância
entre os filmes, d. Assumindo que a rigidez inicial seja
tal que essas alterações sejam pequenas em relação às
dimensões de equilíbrio do sistema, pode-se definir,
novamente para o filme superior, d(V) =d+x, em que x é
o deslocamento médio do filme, com x << d. Isto implica,
porém, que a capacitância do sistema em tela depende
da tensão externa aplicada. O elemento se comporta como
um varactor e, portanto, é não-linear.
Para demonstrar o afirmado, é necessário relacionar
a tensão aplicada com o deslocamento do filme e, portanto,
utilizar um modelo das propriedades mecânicas do sistema.
Esse modelamento mecânico não é o objetivo do presente
artigo e apresenta, em si, uma série de desdobramentos
interessantes por sua combinação de deformação estrutural
e força pneumática, e será apresentado em uma futura
publicação (Basso, a ser submetido). Portanto, a resposta
mecânica a uma excitação elétrica estática será analisada
na aproximação elástica linear, em que então:
(3)
⎠
1
V
2t
+d
sr
I
F0 + ?F
- - - +
+
+
- - - +
+
+
- - - - +
+
+
+
x
?2
-
??
- - - - +
+
+
+
+
Figura 3
Minerva, 6(3): 287-292
290
BASSO
H
H
δF (V ) Aσ 1 2t (ε r + 1) + dε r (ε r − 1)
=
x (V ) =
Vxˆ
k
k
(2t + dε r )2
(6)
com k como constante elástica do filme. Portanto, a
capacitância total do sistema será:
C (V ) = Aε r ε 0
1
1
≈ Aε r ε 0
2t + dε r + ε r x(V )
2t + dε r
⎞
⎛
⎜1 + ε r Aσ 1 2t (ε r + 1) + dε r (ε r − 1)V ⎟
⎟
⎜
k
(2t + dε r )3
⎠
⎝
V0
1
ω 02 − ω 2 + jωΓ
e
jω t
V0 +
(8)
2t (ε r + 1) + dε r (ε r − 1) ⎞
⎛ εr
⎜1 + σ 1
⎟
t
ρ
(2t + dε r )3
⎜
⎟
~
1
C (t ) = Aε r ε 0
⎜
⎟ (9)
2
2
ω0 − ω − jωΓ
2t + dε r ⎜
jωt
⎟
V0
e
⎜
⎟
2
2
2 2
(
)
−
+
Γ
ω
ω
ω
0
⎝
⎠
)
A Impedância com Ponte Balanceada do
Ferroeletreto
Na técnica de medida de impedância com ponte
autobalanceada, a frequência de uma fonte senoidal de
amplitude constante é varrida enquanto se mede a corrente
através do circuito, I, mantendo-se um dos pontos em terra
virtual. A medida de corrente é feita através de um circuito
conversor I-V, e a impedância analisada é determinada
pela razão entre a tensão aplicada no elemento Vx e a tensão
de saída do conversor I-V, V = I/Rr, em que Rr é uma
resistência de referência, através de um voltímetro vetorial
(medida de módulo e fase) (Agilent, 2009). A fase é
determinada através de um detetor de fase, um circuito
que mistura ao sinal uma referência com amplitude unitária
em fase e fora de fase com a excitação. A saída do circuito
misturador (um multiplicador analógico) é composta por
uma parte oscilante e uma parte contínua, ambas proporcionais à tensão medida, mas a parte oscilante é eliminada
por um filtro passa-baixa. Para elementos lineares, por
exemplo, uma associação em paralelo de um capacitor
Minerva, 6(3): 287-292
e
1
(G + jωC )V0 e jωt 1e jωt = 1 (G + jωC )V0 +
R
Rr
Rr
(7)
em que ρ é a densidade do filme, ω0 a frequência de
ressonância natural e Γ a razão entre a impedância mecânica
e a massa deslocada. A capacitância total complexa passa
ser expressa como:
(
V x = V0 e jωt 1e jωt = V0 + V0 e j 2ωt ⇒ V0
Vr =
e a aproximação apresentada é válida dentro das condições
discutidas anteriormente.
No caso de uma excitação harmônica de frequência
angular ω e amplitude V0, V = V0 ejωt, tanto a inércia quanto
o amortecimento, normalmente viscoso, são considerados
resultando para a amplitude complexa x(t):
2t (ε r + 1) + dε r (ε r − 1)
1
~
x (t ) = − σ 1
ρt
(2t + dε r )2
C e um resistor com condutância G, as saídas do voltímetro
vetorial serão:
1
(G + jωC )V0 e j 2ωt ⇒ 1 (G + jωC )V0
Rr
Rr
A razão Rr Vr/Vx fornece a impedância da associação.
A ponte autobalanceada, porém, apresenta algumas
limitações em seu uso em virtude das restrições dos
componentes empregados. Um dos problemas é a existência
de harmônicos na onda de excitação gerada e, consequentemente, no sinal de referência para o misturador.
A saída típica de tensão pode ser expressa por:
~
V (t ) =
∑
∞
n =1
~
Vn e jnωt
(10)
em que as amplitudes dos harmônicos decaem com a ordem
e o segundo harmônico é tipicamente 100 vezes menor
que o primeiro. Para a análise de elementos lineares, o
harmônico de segunda ordem pode ser descartado, já que
a corrente através daqueles resulta em uma série similar
à da equação 10, e a parte constante total de Vr do primeiro
e segundo harmônicos será:
Vr =
1
(G + jωC )V1 + 1 (G + jωC )v2V2
Rr
Rr
em que v2 (<<1) é a componente da referência em segundo
harmônico e a parte medida em Vx será V x = V1 + V2 v 2 ,
significando que Rr Vr/Vx resulta:
(G +
jωC )
V1 + v 2V2
= (G + jωC )
(V1 + V2 v2 )
que é exatamente o resultado anterior.
No caso dos ferroeletretos, porém, a situação é outra.
Como há variação da capacitância com a tensão aplicada
no tempo, a expressão para a corrente através do circuito
fica:
Q = CV ⇒ I =
dQ
dV
dC
=C
+V
dt
dt
dt
(11)
em que V é dado pela equação 10. Retendo até o segundo
harmônico e junto com a equação 9, a corrente total será:
(
)(
)δCjωe
)
I (t ) = C0 + δCe jωt jωV1e jωt + j 2ωV2 e j 2ωt +
(
+ V1e
jωt
+ V2 e
j 2ωt
jωt
(12)
em que os coeficientes C0 e δC estão relacionados com o
fatores fornecidos anteriormente e são listados no Apêndice
1. Da equação 12 obtêm-se:
CARACTERIZAÇÃO DE FERROELETRETOS POR PONTES AUTOBALANCEADAS
I (t ) = jωC 0V1e jωt + ( j 2ωC0V2 + j 2ωδCV1 )e j 2ωt +
+ ( j 3ωδCV2 )e j 3ωt
(13)
O primeiro termo da equação 13 é exatamente o termo
de corrente de um capacitor normal, mas o segundo e o
terceiro termos envolvem a resposta de um capacitor e
as alterações criadas pela deformação do ferroeletreto, e são
não-linear em frequência. Na medida com uma ponte
autobalanceada com distorção da excitação resulta para Vr:
1
+ ( j 2ωC0V2 + j 2ωδCV1 )
Rr
Conclusão
vr
1
+ ( j 3ωδCV2 )
Rr
Rr
⇒ Vr =
+
1
jωC 0 (V1 + 2V2 vr ) +
Rr
(14)
1
jωδC (2V1vr + 3V2 )
Rr
∴ Vr ≈
1
1
jωC 0V1 +
jωδC (2V1vr + 3V2 )
Rr
Rr
enquanto para Vx: V x = V1 + V2 v 2 ≈ V1 , o que resulta para
Rr Vr/Vx:
⎛
V
RrVr / V x ≈ jωC0 + jωδC ⎜⎜ 2vr + 3 2
V1
⎝
⎞
⎟⎟ ≈
⎠
⎛
δC
⎛ V 2 ⎞ ⎞⎟
≈ jωC0 ⎜⎜1 + 2
max⎜ vr ;
⎟
C0
⎝ V 1 ⎠ ⎟⎠
⎝
C' (F)
Logo, a medida de impedância de um ferroeletreto
com a ponte autobalanceada deveria fornecer somente
o termo capacitivo normal. As variações reportadas nos
trabalhos publicados decorrem da existência de segundo
harmônico na excitação e/ou na medida das tensões da
amostra. Um ajuste, utilizando a equação 15, dos resultados
apresentados na Figura 1 pode ser visto na Figura 4 a
seguir, em que a linha mais escura indica as curvas geradas
pelo ajuste.
(15)
Demonstrou-se neste trabalho que, em virtude do
caráter não-linear da impedância de ferroeletretos, sua
caracterização por ponte autobalanceada só é possível
quando esta apresenta componente de segundo harmônico,
no mínimo, na excitação ou na medida do sinal, ou seja,
a ponte autobalanceada não é o equipamento adequado
para caracterizar quantitativamente ferroeletretos,
excetuando algumas características mecânicas dinâmicas
tais como frequência de ressonância e meia-largura do
pico de ressonância. Essa conclusão decorre do modelamento elétrico e mecânico de um ferroeletreto simples,
porém que respeita a característica geral desse tipo de
material.
Por outro lado, fica claro quais as características
desejáveis em um equipamento para medida da razão
corrente/tensão em função da frequência para um
ferroeletreto. Corretamente determinada, essa razão pode
caracterizar quantitativamente vários parâmetros internos
do material.
Este trabalho contou com o suporte financeiro da
Capes, dentro do programa Probral.
95,05p
0
95,00p
–50f
94,95p
–100f
94,90p
–150f
94,85p
–200f
94,80p
–250f
94,75p
0
100k
200k
300k
400k
500k
C" (F)
Vr = jωC 0V1
291
–300f
600k
w (rad/s)
Figura 4
Minerva, 6(3): 287-292
292
BASSO
Apêndice 1
Referências Bibliográficas
1) Relação entre os parâmetros do ferroeletreto e os
coeficientes C0 e δC:
AGILENT IMPEDANCE MEASUREMENT HANDBOOK.
4. ed. 2009.
ALTAFIM, R. A. C. et al. Piezoelectrets form thermoformed bubble structures of fluoropolymer-electret films.
IEEE Transactions on Dielectrics and Electrical Insulation,
v. 13, p. 979-985, 2006.
BASSO, H. C. et al. Three-layer ferroelectrets from perforated
Teflon -PTFE films fused between two homogeneous Teflon
-FEP films. In: IEEE CONFERENCE ON ELECTRICAL
INSULATION AND DIELECTRIC PHENOMENA (CEIDP),
2007, Vancouver, BC. Vancouver: CEIDP – Annual Report
Conference on Electrical Insulation and Dielectric Phenomena,
2007.
GERHARD-MULTHAUPT, R. Less can be more: holes in
polymers lead to a new paradigm of piezoelectric materials
for electret transducers. IEEE Transactions on Dielectrics
and Electrical Insulation, v. 9, p. 850-859, 2002.
MELLINGER, A. Dielectric ressonance spectroscopy:
a versatile tool in the quest for better piezoelectric polymers.
IEEE Transactions on Dielectrics and Electrical Insulation,
v. 10, p. 842-861, 2003.
SESSLER, G. M. (Ed.). Electrets. 2. ed. Stuttgart: Springer
Verlag, 1987. (Série Topics in applied physics v. 33).
C0 = Aε 0
1
2t + dε r
δC = Aε 0
1
2t + dε r
(
(ω
ω02
2
0
− ω 2 − j ωΓ
−ω
εr
σ
ρt 1
)V
) + (ωΓ )
2 2
2t (ε r + 1) + dε r (ε r − 1)
(2t + dε r )3
1
2
2) Relação entre os valores de C’e C” e os parâmetros
do ferroeletreto:
C ' = C0 + Re(δC ) = Aε 0
1
2t + dε r
⎛ ε
⎞
ω 02 − ω 2
⎜1 + r σ 2t (ε r + 1) + dε r (ε r − 1)
⎟
V
1
1
⎜ ρt
⎟
2
2
2 2
t + dε r )3
(
2
(
)
ω
ω
ω
−
+
Γ
0
⎝
⎠
(
C ´´ = Im(δC ) = − Aε 0ε r
(
ω 02
ωΓ
−ω
) + (ωΓ )
2 2
2
V1
Minerva, 6(3): 287-292
)
2t (ε r + 1) + dε r (ε r − 1)
1
σ1
pt
(2t + dε r )4