sen 30 cos 60 0,5 cos 30 sen 60 0,9 ° = ° = ° = ° ≈

1. (Fuvest 2014) Para passar de uma margem a outra de um rio,
uma pessoa se pendura na extremidade de um cipó esticado,
formando um ângulo de 30° com a vertical, e inicia, com
velocidade nula, um movimento pendular. Do outro lado do rio,
a pessoa se solta do cipó no instante em que sua velocidade fica
novamente igual a zero. Imediatamente antes de se soltar, sua
aceleração tem
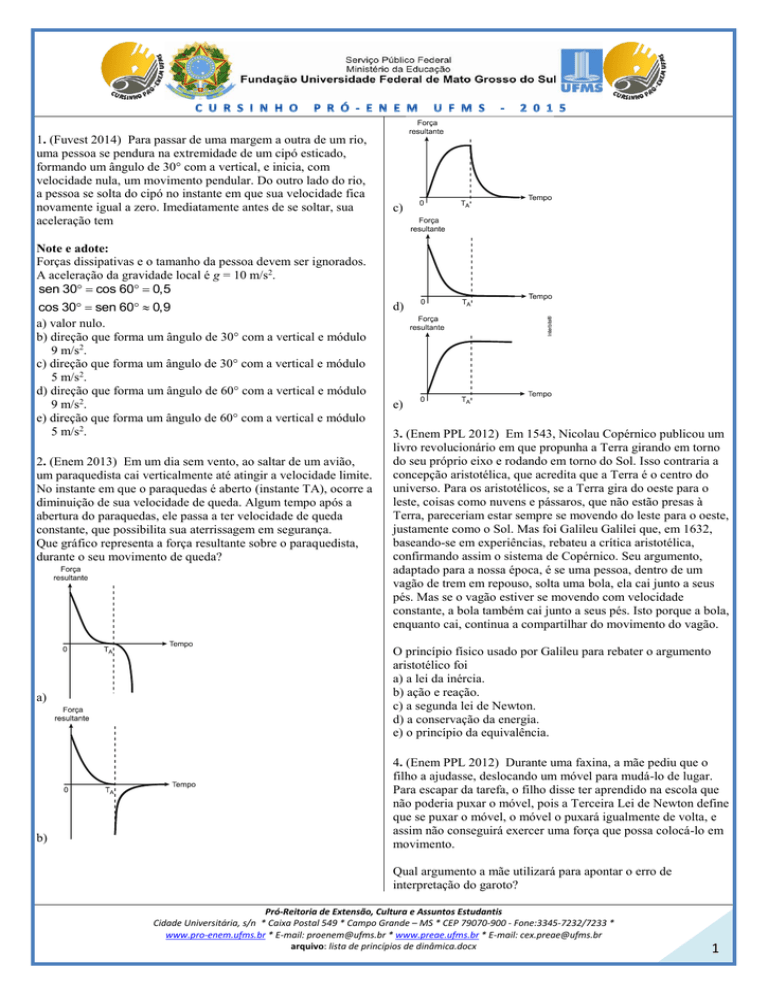
c)
Note e adote:
Forças dissipativas e o tamanho da pessoa devem ser ignorados.
A aceleração da gravidade local é g = 10 m/s2.
sen 30  cos 60  0,5
cos 30  sen 60  0,9
a) valor nulo.
b) direção que forma um ângulo de 30° com a vertical e módulo
9 m/s2.
c) direção que forma um ângulo de 30° com a vertical e módulo
5 m/s2.
d) direção que forma um ângulo de 60° com a vertical e módulo
9 m/s2.
e) direção que forma um ângulo de 60° com a vertical e módulo
5 m/s2.
2. (Enem 2013) Em um dia sem vento, ao saltar de um avião,
um paraquedista cai verticalmente até atingir a velocidade limite.
No instante em que o paraquedas é aberto (instante TA), ocorre a
diminuição de sua velocidade de queda. Algum tempo após a
abertura do paraquedas, ele passa a ter velocidade de queda
constante, que possibilita sua aterrissagem em segurança.
Que gráfico representa a força resultante sobre o paraquedista,
durante o seu movimento de queda?
a)
b)
d)
e)
3. (Enem PPL 2012) Em 1543, Nicolau Copérnico publicou um
livro revolucionário em que propunha a Terra girando em torno
do seu próprio eixo e rodando em torno do Sol. Isso contraria a
concepção aristotélica, que acredita que a Terra é o centro do
universo. Para os aristotélicos, se a Terra gira do oeste para o
leste, coisas como nuvens e pássaros, que não estão presas à
Terra, pareceriam estar sempre se movendo do leste para o oeste,
justamente como o Sol. Mas foi Galileu Galilei que, em 1632,
baseando-se em experiências, rebateu a crítica aristotélica,
confirmando assim o sistema de Copérnico. Seu argumento,
adaptado para a nossa época, é se uma pessoa, dentro de um
vagão de trem em repouso, solta uma bola, ela cai junto a seus
pés. Mas se o vagão estiver se movendo com velocidade
constante, a bola também cai junto a seus pés. Isto porque a bola,
enquanto cai, continua a compartilhar do movimento do vagão.
O princípio físico usado por Galileu para rebater o argumento
aristotélico foi
a) a lei da inércia.
b) ação e reação.
c) a segunda lei de Newton.
d) a conservação da energia.
e) o princípio da equivalência.
4. (Enem PPL 2012) Durante uma faxina, a mãe pediu que o
filho a ajudasse, deslocando um móvel para mudá-lo de lugar.
Para escapar da tarefa, o filho disse ter aprendido na escola que
não poderia puxar o móvel, pois a Terceira Lei de Newton define
que se puxar o móvel, o móvel o puxará igualmente de volta, e
assim não conseguirá exercer uma força que possa colocá-lo em
movimento.
Qual argumento a mãe utilizará para apontar o erro de
interpretação do garoto?
Pró-Reitoria de Extensão, Cultura e Assuntos Estudantis
Cidade Universitária, s/n * Caixa Postal 549 * Campo Grande – MS * CEP 79070-900 - Fone:3345-7232/7233 *
www.pro-enem.ufms.br * E-mail: [email protected] * www.preae.ufms.br * E-mail: [email protected]
arquivo: lista de princípios de dinâmica.docx
1
a) A força de ação é aquela exercida pelo garoto.
b) A força resultante sobre o móvel é sempre nula.
c) As forças que o chão exerce sobre o garoto se anulam.
d) A força de ação é um pouco maior que a força de reação.
e) O par de forças de ação e reação não atua em um mesmo
corpo.
5. (Fuvest 2012) O gráfico abaixo representa a força F exercida
pela musculatura eretora sobre a coluna vertebral, ao se levantar
um peso, em função do ângulo  , entre a direção da coluna e a
horizontal. Ao se levantar pesos com postura incorreta, essa
força pode se tornar muito grande, causando dores lombares e
problemas na coluna.
Com base nas informações dadas e no gráfico acima, foram
feitas as seguintes afirmações:
I. Quanto menor o valor de  , maior o peso que se consegue
levantar.
II. Para evitar problemas na coluna, um halterofilista deve
procurar levantar pesos adotando postura corporal cujo ângulo
 seja grande.
III. Quanto maior o valor de  , menor a tensão na musculatura
eretora ao se levantar um peso.
Está correto apenas o que se afirma em
a) I.
b) II.
c) III.
d) I e II.
e) II e III.
A explicação para a necessidade do uso da engrenagem com
trava é:
a) O travamento do motor, para que ele não se solte
aleatoriamente.
b) A seleção da velocidade, controlada pela pressão nos dentes
da engrenagem.
c) O controle do sentido da velocidade tangencial, permitindo,
inclusive, uma fácil leitura do seu valor.
d) A determinação do movimento, devido ao caráter aleatório,
cuja tendência é o equilíbrio.
e) A escolha do ângulo a ser girado, sendo possível, inclusive,
medi-lo pelo número de dentes da engrenagem.
7. (Enem 2009) O ônibus espacial Atlantis foi lançado ao espaço
com cinco astronautas a bordo e uma câmera nova, que iria
substituir uma outra danificada por um curto-circuito no
telescópio Hubble. Depois de entrarem em órbita a 560 km de
altura, os astronautas se aproximaram do Hubble. Dois
astronautas saíram da Atlantis e se dirigiram ao telescópio.
Ao abrir a porta de acesso, um deles exclamou: “Esse telescópio
tem a massa grande, mas o peso é pequeno.”
6. (Enem 2011) Partículas suspensas em um fluido apresentam
contínua movimentação aleatória, chamado movimento
browniano, causado pelos choques das partículas que compõe o
fluido. A ideia de um inventor era construir uma série de
palhetas, montadas sobre um eixo, que seriam postas em
movimento pela agitação das partículas ao seu redor. Como o
movimento ocorreria igualmente em ambos os sentidos de
rotação, o cientista concebeu um segundo elemento, um dente de
engrenagem assimétrico. Assim, em escala muito pequena, este
tipo de motor poderia executar trabalho, por exemplo, puxando
um pequeno peso para cima. O esquema, que já foi testado, é
mostrado a seguir.
Considerando o texto e as leis de Kepler, pode-se afirmar que a
frase dita pelo astronauta
Pró-Reitoria de Extensão, Cultura e Assuntos Estudantis
Cidade Universitária, s/n * Caixa Postal 549 * Campo Grande – MS * CEP 79070-900 - Fone:3345-7232/7233 *
www.pro-enem.ufms.br * E-mail: [email protected] * www.preae.ufms.br * E-mail: [email protected]
arquivo: lista de princípios de dinâmica.docx
2
a) se justifica porque o tamanho do telescópio determina a sua
massa, enquanto seu pequeno peso decorre da falta de ação da
aceleração da gravidade.
b) se justifica ao verificar que a inércia do telescópio é grande
comparada à dele próprio, e que o peso do telescópio é
pequeno porque a atração gravitacional criada por sua massa
era pequena.
c) não se justifica, porque a avaliação da massa e do peso de
objetos em órbita tem por base as leis de Kepler, que não se
aplicam a satélites artificiais.
d) não se justifica, porque a força-peso é a força exercida pela
gravidade terrestre, neste caso, sobre o telescópio e é a
responsável por manter o próprio telescópio em órbita.
e) não se justifica, pois a ação da força-peso implica a ação de
uma força de reação contrária, que não existe naquele
ambiente. A massa do telescópio poderia ser avaliada
simplesmente pelo seu volume.
8. (Fuvest 1996) Dois vagões de massa M1 e M2 estão
interligados por uma mola de massa desprezível e o conjunto é
puxado ao longo de trilhos retilíneos e horizontais por uma força
que tem a direção dos trilhos. Tanto o módulo da força quanto o
comprimento da mola podem variar com o tempo. Num
determinado instante os módulos da força e da aceleração do
vagão de massa M1 valem, respectivamente F e a1, tendo ambas o
mesmo sentido. O módulo da aceleração do vagão de massa M 2
nesse mesmo instante, vale
a)
F
 M1a1 
M2
b)
F
.
M1  M2 
c)
F
.
M2
9. (Fuvest 1991) Adote: g = 10 m/s2
Um homem tenta levantar uma caixa de 5 kg, que está sobre uma
mesa, aplicando uma força vertical de 10 N. Nesta situação, o
valor da força que a mesa aplica na caixa é:
a) 0 N
b) 5 N
c) 10 N
d) 40 N
e) 50 N
10. (Fuvest 1991) Adote: g = 10 m/s2
As duas forças que agem sobre uma gota de chuva, a força peso e
a força devida à resistência do ar, têm mesma direção e sentidos
opostos. A partir da altura de 125 m acima do solo, estando a
gota com uma velocidade de 8m/s, essas duas forças passam a ter
o mesmo módulo. A gota atinge o solo com a velocidade de:
a) 8 m/s
b) 35 m/s
c) 42 m/s
d) 50 m/s
e) 58 m/s
11. (Fuvest 1990) Um garoto segura uma bexiga de 10 g, cheia
de gás, exercendo sobre o barbante uma força para baixo de
intensidade 0,1 N. Nestas condições:
.
 F 
 - a1.
 M2 
d) 
 F 
 + a1.
 M2 
e) 
Pró-Reitoria de Extensão, Cultura e Assuntos Estudantis
Cidade Universitária, s/n * Caixa Postal 549 * Campo Grande – MS * CEP 79070-900 - Fone:3345-7232/7233 *
www.pro-enem.ufms.br * E-mail: [email protected] * www.preae.ufms.br * E-mail: [email protected]
arquivo: lista de princípios de dinâmica.docx
3
a) a pressão no interior da bexiga é menor que a pressão
atmosférica local.
b) a pressão no interior da bexiga é igual à pressão atmosférica
local.
c) o empuxo que a bexiga sofre vale 0,1 N.
d) a densidade média da bexiga é menor que a do ar que a
envolve.
e) a densidade média da bexiga é maior que a do ar que a
envolve.
12. (Fuvest 1990) Um corpo de 3 kg move-se, sem atrito, num
plano horizontal, sob a ação de uma força horizontal constante de
intensidade 7 N. No instante t0 sua velocidade é nula. No instante
t1 > t0 a velocidade é 21 m/s.
Calcule ∆t = t1 - t0.
a) 3 s.
b) 9 s.
c) 12 s.
d) 16 s.
e) 21 s.
Se a velocidade horizontal antes da manobra era de 18,0 km/h e
foi mantida, supondo que a subida tenha se dado com velocidade
constante de 0,9 km/h, o deslocamento horizontal que a nave
realizou, do momento em que o timoneiro iniciou a operação até
o instante em que a nau chegou à superfície foi, em m, de
a) 4 800.
b) 3 000.
c) 2 500.
d) 1 600.
e) 1 200.
15. (Ufscar 2000) Nos esquemas estão representadas a
velocidade v e a aceleração a do ponto material P. Assinale a
alternativa em que o módulo da velocidade desse ponto material
permanece constante.
13. (Fuvest 1989) No mês de agosto de 1988, o planeta Marte
teve a máxima aproximação da Terra. Nesse dia as pessoas, ao
observarem o planeta, estavam vendo a luz emitida pelo Sol
algum tempo antes. Aproximadamente quanto tempo antes?
Considere as órbitas da Terra e de Marte circulares e coplanares,
com raios de 150.000.000 km e 231.000.000 km,
respectivamente.
a) 81 anos-luz
b) 2 horas
c) 30 segundos
d) 8 minutos
e) 17 minutos
14. (Ufscar 2007) O submarino navegava com velocidade
constante, nivelado a 150 m de profundidade, quando seu capitão
decide levar lentamente a embarcação à tona, sem contudo
abandonar o movimento à frente. Comunica a intenção ao
timoneiro, que procede ao esvaziamento dos tanques de lastro,
controlando-os de tal modo que a velocidade de subida da nave
fosse constante.
Pró-Reitoria de Extensão, Cultura e Assuntos Estudantis
Cidade Universitária, s/n * Caixa Postal 549 * Campo Grande – MS * CEP 79070-900 - Fone:3345-7232/7233 *
www.pro-enem.ufms.br * E-mail: [email protected] * www.preae.ufms.br * E-mail: [email protected]
arquivo: lista de princípios de dinâmica.docx
4
Gabarito:
[E]
Resposta da questão 1:
[E]
Ação e reação são forças de mesma intensidade, mesma direção
e sentidos opostos, porém, não se equilibram, pois não atuam no
mesmo corpo.
Se a velocidade é nula, a aceleração (a) tem direção tangencial,
formando com a vertical ângulo de 60°, como indicado na figura.
Resposta da questão 5:
[E]
Analisando cada uma das afirmações:
I. Incorreta. Quando menor o ângulo  , mais inclinada está a
pessoa, exigindo maior esforço da coluna, portanto menor o peso
que se consegue levantar.
II. Correta. Quanto maior o ângulo  , mais ereto está o
halterofilista, exigindo menor esforço da coluna.
III. Correta. Quanto maior o valor de  , menor a tensão na
musculatura eretora ao se levantar um peso, que é exatamente o
que mostra o gráfico.
Resposta da questão 6:
[D]
A resultante é a componente tangencial do peso. Aplicando o
Princípio Fundamental da Dinâmica:
 1
Px  m a  m gcos 60  m a  a  10   
2
a  5 m/s2 .
Resposta da questão 2:
[B]
No início da queda, a única força atuante sobre o paraquedista
(homem + paraquedas) é apenas o peso [para baixo (+)]. À
medida que acelera, aumenta a força de resistência do ar, até que
a resultante se anula, quando é atingida a velocidade limite. No
instante (TA) em que o paraquedas é aberto, a força de resistência
do ar aumenta abruptamente, ficando mais intensa que o peso,
invertendo o sentido da resultante [para cima (-)]. O movimento
passa a ser retardado até ser atingida a nova velocidade limite,
quando a resultante volta a ser nula.
Resposta da questão 3:
[A]
A lei de inércia afirma que um corpo tende sempre a manter seu
estado de movimento ou de repouso. Manterá se a resultante das
forças sobre ele for nula. No caso da bola solta dentro do vagão,
a resultante das forças horizontais é nula, então, por inércia, ela
mantém a componente horizontal de sua velocidade, caindo junto
aos pés da pessoa.
Como o movimento é caótico (em todos os sentidos), sem a
trava, a engrenagem ficaria oscilando, não girando em sentido
algum.
Resposta da questão 7:
[D]
De fato, as leis de Kepler não justificam a afirmação do
astronauta porque elas versam sobre forma da órbita, período da
órbita e área varrida na órbita. Essa afirmação explica-se pelo
Princípio Fundamental da Dinâmica, pois o que está em questão
são a massa e o peso do telescópio. Como o astronauta e o
telescópio estão em órbita, estão sujeitos apenas à força peso, e,
consequentemente, à mesma aceleração (centrípeta), que é a da
gravidade local, tendo peso APARENTE nulo.
R = P  m a = m g  a = g.
É pelo mesmo motivo que os objetos flutuam dentro de uma
nave. Em Física, diz-se nesse caso que os corpos estão em estado
de imponderabilidade.
Apenas para complementar: considerando R = 6.400 km o raio
da Terra, à altura h = 540 km, o raio da órbita do telescópio é r =
R + h = 6.400 + 540 = 6.940 km. De acordo com a lei de Newton
da gravitação, a intensidade do campo gravitacional num ponto
2
R
da órbita é g = g0  r  , sendo g0 = 10 m/s2. Assim,
2
 6.400 
g  10 
 8,5 m/s2 . Ou seja, o peso REAL do

 6.940 
telescópio na órbita é 85% do seu peso na superfície terrestre.
Resposta da questão 4:
Pró-Reitoria de Extensão, Cultura e Assuntos Estudantis
Cidade Universitária, s/n * Caixa Postal 549 * Campo Grande – MS * CEP 79070-900 - Fone:3345-7232/7233 *
www.pro-enem.ufms.br * E-mail: [email protected] * www.preae.ufms.br * E-mail: [email protected]
arquivo: lista de princípios de dinâmica.docx
5
Resposta da questão 8:
[A]
Resposta da questão 9:
[D]
Resposta da questão 10:
[A]
Resposta da questão 11:
[D]
Resposta da questão 12:
[B]
Resposta da questão 13:
[E]
Resposta da questão 14:
[B]
Resolução:
Pelo princípio de Galileu os movimentos são independentes.
Movimento Vertical
Vy  0,9km / h 
Vy 
Sy
t
0,9
m / s  0,25m / s
3,6
 0,25 
150
 t  600s
t
Movimento Horizontal
VX  18km / h 
VX 
18
m / s  5m / s
3,6
S X
S X
5
 S X  3.000m
t
600
Resposta da questão 15:
[C]
Pró-Reitoria de Extensão, Cultura e Assuntos Estudantis
Cidade Universitária, s/n * Caixa Postal 549 * Campo Grande – MS * CEP 79070-900 - Fone:3345-7232/7233 *
www.pro-enem.ufms.br * E-mail: [email protected] * www.preae.ufms.br * E-mail: [email protected]
arquivo: lista de princípios de dinâmica.docx
6