Física - Etapa

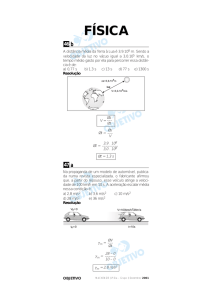
Questão 46
A distância média da Terra à Lua é
3,9 ⋅ 108 m. Sendo a velocidade da luz no vácuo igual a 3,0 ⋅ 105 km/s, o tempo médio gasto por ela para percorrer essa distância é de:
a) 0,77 s
b) 1,3 s
c) 13 s
d) 77 s
e) 1 300 s
Dados: cos α = 0,8, sen α = 0,6 e g = 10 m/s2
a) 2,3 m/s2
d) 7,0 m/s2
alternativa B
Como a velocidade (c) da luz no vácuo é constante e c = 3,0 ⋅ 10 5 km/s = 3,0 ⋅ 10 8 m/s, o tempo
(t) médio gasto por ela é dado por:
t =
d
3,9 ⋅ 10 8
=
⇒
c
3,0 ⋅ 10 8
b) 4,0 m/s2
e) 8,7 m/s2
c) 6,2 m/s2
alternativa B
As forças que atuam sobre o corpo são dadas
por:
t = 1,3 s
Questão 47
Na propaganda de um modelo de automóvel,
publicada numa revista especializada, o fabricante afirmou que, a partir do repouso,
esse veículo atinge a velocidade de 100 km/h
em 10 s. A aceleração escalar média nessa
condição é:
a) 2,8 m/s2
b) 3,6 m/s2
c) 10 m/s2
2
2
d) 28 m/s
e) 36 m/s
alternativa A
Da definição de aceleração escalar média (am ),
100
sendo v = 100 km/h =
m/s, temos:
3,6
0 100
∆v v − v 0
3,6
=
am =
=
⇒ am = 2,8 m/s 2
∆t
10
∆t
Questão 48
Um corpo de 4 kg desloca-se com movimento
retilíneo uniformemente acelerado, apoiado
sobre uma superfície horizontal e lisa, devido
à ação da força F. A reação da superfície de
apoio sobre o corpo tem intensidade 28 N. A
aceleração escalar desse corpo vale:
Como a resultante das forças na vertical é nula,
temos:
F ⋅ senα + N = P ⇒ F ⋅ 0,6 + 28 = 40 ⇒ F = 20 N
Na horizontal, do Princípio Fundamental da Dinâmica, vem:
R = m ⋅ γ ⇒ F ⋅ cosα = m ⋅ γ ⇒ 20 ⋅ 0,8 = 4 ⋅ γ ⇒
⇒
γ = 4,0 m/s 2
Questão 49
Um corpo é lançado do solo, verticalmente
para cima, com velocidade de 8 m/s. Nesse local a resistência do ar é desprezível e a aceleração da gravidade tem módulo 10 m/s2 . No
instante em que a energia cinética desse corpo é igual à metade da que possuía no lançamento, ele se encontra a uma altura de:
a) 3,2 m
b) 2,4 m
c) 2,0 m
d) 1,6 m
e) 1,2 m
alternativa D
Sendo o sistema conservativo, e admitindo E g = 0
para a posição do lançamento, temos:
física 2
inicial
final
Em
= Em
mv 2
1  mv 2 
1 inicial ⇒ 2 = mgh + 2  2  ⇒
final


E
Ec
=
2 c
⇒
82
1
82
= 10h +
⋅
⇒
2
2
2
h = 1,6 m
ra. Considerando que a massa dessa gangorra está distribuída uniformemente, as posições em que as crianças se mantêm em equilíbrio na direção horizontal estão melhor representadas na figura:
Questão 50
Em um experimento verificamos que certo
corpúsculo descreve um movimento circular
uniforme de raio 6 m, percorrendo 96 m em
4 s. O período do movimento desse corpúsculo é aproximadamente:
a) 0,8 s b) 1,0 s c) 1,2 s d) 1,6 s e) 2,4 s
a)
alternativa D
Admitindo-se π = 3,14, temos que o período do
movimento do corpúsculo é dado por:
2 πR
V =
2 πR∆t
T
⇒T =
⇒
∆S
∆S
V =
∆t
⇒T =
b)
2 ⋅ 3,14 ⋅ 6 ⋅ 4
⇒ T = 1,6 s
96
Questão 51
Uma pessoa mediu a temperatura de seu corpo, utilizando-se de um termômetro graduado
na escala Fahrenheit, e encontrou o valor
97,7 o F. Essa temperatura, na escala Celsius,
corresponde a:
a) 36,5 oC
b) 37,0 oC
c) 37,5 oC
d) 38,0 oC
c)
d)
e) 38,5 oC
alternativa A
A relação entre as escalas é dada por:
θC
θ − 32
θ
97,7 − 32
= F
⇒ C =
⇒
5
9
5
9
o
⇒ θC = 36,5 C
Questão 52
Três crianças de massas 20 kg, 30 kg e 50 kg
estão brincando juntas numa mesma gangor-
e)
física 3
alternativa B
Vamos admitir a seguinte condição de equilíbrio:
Questão 54
Um mol de gás ideal encontra-se inicialmente
(estado A) nas C.N.T.P.. Em seguida esse gás
sofre duas transformações sucessivas, conforme mostra o diagrama P x V a seguir. O volume ocupado pelo gás no estado C é:
Sendo g a aceleração da gravidade, no equilíbrio,
para a gangorra, temos:
M R (O) = 0 ⇒ 50 ⋅ g ⋅ L =
= 20 ⋅ g ⋅ 1,0 + 30 ⋅ g(1,0 + 1,0) ⇒ L = 1,6 m
Portanto, a criança de massa 50 kg está a
2,0 − 1,6 = 0,4 m da extremidade da gangorra.
Essa posição está representada na figura da alternativa B.
Questão 53
Por um aquecedor a gás passam 15 litros de
água por minuto. Para que a temperatura da
água se eleve de 25 o C, a potência calorífica
útil do aquecedor deve ser:
Dados:
Dado: R = 0,082 (atm ⋅ litro)/(mol ⋅ K)
a) 11,2 litros.
c) 22,4 litros.
e) 44,8 litros.
Calor específico da água = 1 cal/g.o C
Massa específica da água = 1 kg/litro
a) 12 500 kcal/h
c) 22 500 kcal/h
e) 32 500 kcal/h
b) 18 750 kcal/h
d) 27 250 kcal/h
alternativa C
Sendo a densidade da água igual a
kg
g
, a potência calorífica (P)
µ =1
= 1 ⋅ 10 3
l
l
do aquecedor no intervalo de tempo ∆t = 1 min =
1
h, é dada por:
=
60
µ ⋅ V ⋅ c ⋅ ∆θ
Q
m ⋅ c ⋅ ∆θ
P =
=
=
=
∆t
∆t
∆t
1 ⋅ 10 3 ⋅ 15 ⋅ 1 ⋅ 25
=
⇒ P = 22 500 ⋅10 3 cal/h ⇒
1
60
⇒
P = 22 500 kcal/h
Obs.: a unidade correta de calor específico é
cal/(g ⋅ oC).
b) 16,8 litros.
d) 33,6 litros.
alternativa E
Um mol de um gás ideal ocupa nas CNTP um volume de 22,4 l. Portanto, utilizando a Lei Geral
dos Gases Perfeitos, o volume (VC ) ocupado pelo
gás no estado C é dado por:
PAVA
P V
0,75 ⋅ VC
1,00 ⋅ 22,4
= C C ⇒
=
⇒
TA
TC
273,0
409,5
⇒
VC = 44,8 l
Questão 55
Uma lente biconvexa é:
a) sempre convergente.
b) sempre divergente.
c) convergente somente se o índice de refração absoluto do meio que a envolve for maior
que o índice de refração absoluto do material
que a constitui.
d) convergente somente se o índice de refração absoluto do meio que a envolve for me-
física 4
nor que o índice de refração absoluto do material que a constitui.
e) divergente somente se o índice de refração
absoluto do meio que a envolve for menor que
o índice de refração absoluto do material que
a constitui.
alternativa D
Uma lente biconvexa possui bordas finas e, portanto, é convergente somente se o índice de refração absoluto do meio que a envolve for menor
que o índice de refração absoluto do material que
a constitui.
Questão 56
Considere as seguintes afirmações.
I – As ondas mecânicas não se propagam no
vácuo.
II – As ondas eletromagnéticas se propagam
somente no vácuo.
III – A luz se propaga tanto no vácuo como
em meios materiais, por isso é uma onda eletromecânica.
Assinale:
a) se somente a afirmação I for verdadeira.
b) se somente a afirmação II for verdadeira.
c) se somente as afirmações I e II forem verdadeiras.
d) se somente as afirmações I e III forem verdadeiras.
e) se as três afirmações forem verdadeiras.
alternativa A
I. Verdadeira. Ondas mecânicas necessitam de
um meio material para se propagarem.
II. Falsa. Ondas eletromagnéticas se propagam
no vácuo e também em meios materiais.
III. Falsa. A luz é uma onda eletromagnética.
Questão 57
Nos pontos A e B da figura são colocadas,
respectivamente, as cargas elétricas puntiformes −3Q e +Q. No ponto P o vetor campo
elétrico resultante tem intensidade:
a) k
5Q
12d2
b) k
2Q
9d2
d) k
4Q
3d2
e) k
7Q
18d2
Q
12d2
c) k
alternativa C
Os vetores campo elétrico produzidos no ponto P
pelas cargas colocadas em A e B são mostrados
a seguir:
Assim, temos:
k |Q A |
EA =
(3d) 2
k |QB |
k |QB |
k |Q A |
EB =
⇒ ER =
−
⇒
(3d) 2
(2d) 2
(2d) 2
ER = |E A − EB |
⇒ ER =
k ⋅ 3Q
9d 2
−
k ⋅Q
4d 2
⇒
ER =
kQ
12d 2
Questão 58
A tabela abaixo mostra o tempo de uso diário
de alguns dispositivos elétricos de uma residência. Sendo R$ 0,20 o preço total de 1 kWh
de energia elétrica, o custo mensal (30 dias)
da energia elétrica consumida nesse caso é:
Dispositivo Potência
Quantidade
Tempo de
uso diário
de cada um
Lâmpada
60 W
4
5 horas
Lâmpada
100 W
2
4 horas
Chuveiro
4 000 W
1
0,5 hora
a) R$ 20,00.
d) R$ 26,00.
b) R$ 22,00.
e) R$ 28,00.
c) R$ 24,00.
alternativa C
Como a energia elétrica transformada por 1 aparelho é dada por P ⋅ ∆t, para q aparelhos temos:
física 5
Dispositivo
P
q
∆t
Energia Transformada
por dia (q ⋅ P ⋅ ∆t)
Lâmpada
60 W
4
5h
1 200 W ⋅ h
Lâmpada
100 W
2
4h
800 W ⋅ h
Chuveiro
4 000 W
1
0,5 h
2 000 W ⋅ h
Total diário =
= 4 000 W ⋅ h = 4 kWh
alternativa E
Com a chave aberta e utilizando-se do resistor
equivalente, temos:
U = Req. ⋅ i ⇒ ε = (2,5 R) ⋅ 0,50 ⇒ ε = 1,25 R
Com a chave fechada, os dois resistores em série
estarão em curto-circuito e teremos:
ε = R’eq. ⋅ I ⇒ (1,25 R) = (0,5 R) ⋅ I ⇒
⇒ I = 2,5 A ⇒ LA = 2,5 A
Assim, o custo mensal (30 dias) da energia elétrica transformada é de 30 ⋅ 4 ⋅ 0,20 = R$ 24,00 .
Questão 60
Questão 59
Um fio metálico tem resistência elétrica igual
a 10 Ω. A resistência elétrica de outro fio de
mesmo material, com o dobro do comprimento e dobro do raio da secção transversal, é:
a) 20 Ω
b) 15 Ω
c) 10 Ω
d) 5 Ω
e) 2 Ω
Quatro resistores idênticos estão associados
conforme a ilustração a seguir. O amperímetro e o gerador são ideais. Quando a chave
(Ch) está aberta, o amperímetro assinala a
intensidade de corrente 0,50 A e, quando a
chave está fechada, assinala a intensidade
de corrente:
alternativa D
Para fios homogêneos e de secção circular constante, temos:
l
10 = ρ ⋅
πR 2
l
R =ρ⋅
⇒
⇒
2l
A
R =ρ⋅
π(2R) 2
l
ρ ⋅
2
10
π
R
⇒
=
2l
R
ρ ⋅
π(2R) 2
a) 0,10 A
d) 1,0 A
b) 0,25 A
e) 2,5 A
c) 0,50 A
⇒
R=5Ω
⇒
10
4R 2
=
⇒
R
2R 2