Apresentação do PowerPoint

UNIVERSIDADE DO ESTADO DO RIO DE JANEIRO
INSTITUTO POLITÉCNICO
Graduação em Engenharia Mecânica
Disciplinas:
Mecânica dos Materiais 2 – 6º Período
E
Dinâmica e Projeto de Máquinas 2-10º Período
Professor: Dr. Damiano da Silva Militão.
Tema de aula 8: Fadiga
OBJETIVO:
Apresentar os principais modelos de falha devido a carregamentos dinâmicos cíclicos. (Fadiga)
Estimar as tensões resistidas em peças sujeitas à Fadiga.
SEQUÊNCIA DE ABORDAGENS:
8.1-Estágios e modelos de fadiga
8.2- Resistência à fadiga; para um certo nº de ciclos N (SN) e o limite para uma
vida infinita (Sf)
8.3-Fadiga sob tensão repetida ou flutuante
8.4-Fadiga sob tensão combinada
8.5-Fadiga de contato superficial
8.6-Previsão de fadiga por variação randômica de cargas.
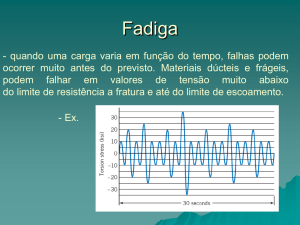
8.1-Estágios e modelos de Fadiga
Mecanismo inicia com trinca invisível que progride até a ruptura brusca após N ciclos de carga, com def.
plástica e sob tensão as vezes abaixo de Srup . Utilizaremos σ ou S p/ tensão neste capítulo.
Quinas, roscas, rasgos, corrosão, entalhes ou furos acumulam tensão e propagam as fissuras.
Estágios de fadiga;
1º Início de trinca:
3ºFratura:
Em dúcteis; vazios sob tração
causam regiões de
concentração de tensão
(entalhes), com os ciclos escoa
em bandas e deslizamento.
Em frágeis; ñ há escoamento,
pode passar direto à
propagação da trinca.
2º Propagação:
Se ‘a’ aumenta até que
Trinca cresce (aumenta ‘a’).
atinja Kc
(Tenacidade à fratura onde
FSFM=Kc/K) ocorre fratura por
fadiga (com marcas de praia).
(amplitudes altas ou corrosão
aumentam a taxa de
crescimento por ciclo)
<-Eixo com chaveta sob flexão rotativa.
Eixo de manivela de motor
sob torção e flexão->
Vejamos alguns padrões de falha:
(Quando é σnom que aumenta,
geralmente falha é estática).
Regimes de fadiga:
FBC: “Fadiga de baixo ciclo” (falha com N<103 com def. plásticas).
FAC: “Fadiga de alto ciclo” (falha com N>103 ou pode ter vida infinita com def. elásticas apenas) .
Modelos de fadiga;
1º Tensão - nº de ciclos(S-N);
• Mais usado p/ FAC;
• Baseado na amplitude de tensão conhecida, visa obter a resistência à fadiga; para um certo nº de ciclos
N (SN) e o limite para uma vida infinita (Sf) .
• A teoria propõe manter tensão baixa em entalhes p/ ñ iniciar escoamento em trincas.
2º Deformação – nº de ciclos;
• Mais usado p/ FBC;
• Baseado na deformação, prevê computacionalmente o início de trinca (estágio 1) em projetos de vida
finita (sob tensões altas que causem escoamento);
3º Abordagem Mecânica da Fratura Linear Elástica (MFLE);
• Usado em FBC;
• Baseia-se em predizer a vida finita restante para a propagação de trinca pré-existentes (estágio 2) (sob
tensões cíclicas elevadas)
• Utiliza
(estima ‘a’ e ‘β’ iniciais para iterações computacionais).
• Usado em ensaios ñ destrutivos (END) aeronáuticos.
Trabalharemos o 1º modelo;
8.2- Resistência à fadiga; para um certo nº de ciclos N (SN) e limite para uma vida infinita (Sf)
Usando o 1º modelo (S-N), submetemos corpos
de prova à ensaios de fadiga por tração, flexão
ou torção (alternadas) ;
Exs: - Máquina flexo-rotativa de Moore;
- Máquina de fadiga por tração-compressão;
http://www.youtube.com/watch?v=XKJtS27DMtY&feature=fvwrel
Analisemos o diagramas (S-N),
para corpos de prova sob flexão; Log SN
(lim. de Fadiga por nº de ciclos do CP)
Ex: P/ Aço na região FAC,
“sob flexão, a literatura
recomenda aprox.
de 0.9 e aprox 0.504 p/
aços de Srup até 1400MPa,
(estimado
experimentalmente)“
Obs:1-P/ demais
materiais ver Norton
pg316
onde;
- Srup é o lim. de ruptura sob tração.
Sf ’ =
-Sf’ é lim. de fadiga para vida infinita
do CP.
Log N
A eq. da reta (p/ pts entre 0.9Srup e 0.5 Srup) è;
onde
e
( Teo. da fadiga
cumulativa de
Fatores modificativos:
Kb; Fator de tamanho da peça;
Minner).
;
Sf ; Lim. de resist. à fadiga vida infinita da peça;
Sf' ;
“
do corpo de prova;
(torção ou flexão)
Ka ; Fator de acabamento superficial;
(a e b em tabela
ou gráfico)
ex:
Kb=1 (tração, ou d<2.79)
(p/ d>254mm usar 0.6 à 0.7)
(p/ seções ñ circulares usar
(A95 =área
da peça à 95% da carga máxima(Norton pg319))
Ex: retângular;
Kc =fator do tipo de carga;
Kd =fator de temperatura;
Tabelados. Ex: aços
rup
Kd=1
Kd=1-0.0058(T-450)
Kd=1-0.0032(T-840)
Ke = Fatores diversos, como concentração de tensões , ambiental, corrosão, tensão residual...
Considerando apenas concentração de tensões->
(q=sensibilidade ao entalhe);
(Kt=fator de concentração de tensão), obtido
experimentalmente fazendo Kt=σmax/σnom,
ou pelas tabelas; Exs:
(Kf=fator efetivo);
(r=raio do entalhe)
( 𝑎=cte Neuber)ex:
rup
rup
Exemplo: Uma barra de aço está sob flexão pura alternada, a)construa o diagrama S-N da peça e defina suas
equações. B) Quantos ciclos de vida podem ser esperados para falhar numa tensão alternada de 100MPa?
Dados: Ke=0.753 (fator diverso de confiabilidade), Srup=600MPa, seção quadrada de 150mm lado, laminada à
quente. Tmáxde operação=500ºC.
(em 106 ciclos)
Sol: a) A região FAC de (S-N) varia linear entre
e 0.9Srup =540MPa (em 103 ciclos);
Para aço: Sf ’=0.5Srup = 0.5(600)=300MPa.
(tabela acab. superficial)
=121.2mm
(fator tamanho “retângulo”)
Kb=0.859-0.000837.121.2≅0.747.
Kd (tabela fator temp.)
Kc=1 (carga flexão)
Ke=0.753 (dado)
Logo:
Sf=0.584(0.747)(1)(0.7)(0.753)(300)=70MPa
Esboçamos o gráfico (S-N)(região FAC e FBC):
As equações serão:
ou
Onde:
Portanto escrevemos a equação:
b) Substituindo a tensão alternada 100MPa na eq. obtemos N para a falha:
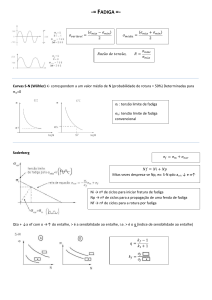
8.3-Fadiga sob tensão repetida ou flutuante
Considerando tensões flutuantes ou repetidas
além das tensões alternadas temos tb tensões médias;
Razão de amplitude: A=σa/σm,
Diagramas;
Goodman (mais usado na engenharia) pressupõe que atuando
apenas σm, falha na Srup, e atuando apenas σa falha na
resistência à fadiga Sf , e une estes pts pela eq. de reta abaixo,
(onde n=F.S);
Gerber (idem, aproximando pela parábola abaixo);
Soderberg mais conservadora usa tensão de escoamto (Sy (ou E))
na abcissa e tb aproxima por reta;
Para quais destas o pt A éstá seguro?
Rescrevendo
incorporando o
F.S teríamos;
Exemplo: A peça de aço é submetida a uma carga fletora F. A mola flutua entre 9,3 kN a 10,67kN. Possui
ruptura Srup=1400Mpa e escoamento Se=950 Mpa. Considerando acabamento de forjamento para a peça,
calcule o fator de segurança (n); a) contra a fadiga e b)contra o escoamento.
Sol: a) Vamos obter n através de Goodman:
No DCL temos:
,
logo M no centro será:
Como F flutua:
A tensão normal de flexão será:
Portanto temos:
assim estimamos as tensões alternada e média;
Resta obter o limite de fadiga Sf da peça;
Para aços
(fatores diversos; concentração de tensão)
rup
(q=sensibilidade ao entalhe);
(Kf=fator efetivo);
(Kt=fator de concentração de tensão)obtido no
gráfico:
Logo
e
(r=raio do entalhe)
( 𝑎=cte Neuber
tabela)onde;
Srup=1400Mpa(/6.89)=203ksi,->
logo ( 𝑎=0.018)
e r=5mm(/25.4)=0.196in
q=1/(1+(0.018/ 0.196))≅ 𝟎. 𝟗𝟓
Finalmente:
rup
é o limite de fadiga da peça
buscado,
Voltando em Goodmam ;
(F.S)
b)Pelo escoamento basta fazer:
rup
8.4-Fadiga sob tensão combinada
Somamos p/ obter tensão única, (alternada σa ou média
σm) nas direções 1 e 2 principais (ou 3D);
Ex:
ou ou
m 2
ou ou
m 2
ou ou
m 2
ou ou
m 2
E escrevemos as tensões equivalentes de Von Mises σ’ ;
ou
nos eixos x-y:
Posteriormente aplicamos Goodman.
.
8.5-Fadiga de contato superficial
Se deve à contato direto entre superfícies.
Ex:dentes de engrenagens, rolamento,etc...
Fazemos
onde:
Ex:
Def:
Ssf lim. de resist. à fadiga superficial da peça.
Ssf ’ lim. de resist. à fadiga superficial do CP. (tabelados)
Ex:
Ssf ’=0,4HB-10 kpsi (para aço de 108 ciclos de vida útil)
p/ 104<N<108.
(Ex: CH=1 para superfícies de durezas iguais).
(Ex: CT=1 para lubrificantes a menos de 120º)
tema considerado.
. Depende do sisEx: P/ engrenagens;
Obtida Ssf , relacionamos com
a tensão aplicada na peça e o
coef. de segurança.
8.6-Previsão de fadiga por variação randômica de cargas.
-> ni é a qtdd de ciclos sofridos ao nível de tensão que falharia com Ni ciclos no
diagrama (S-N).
Equacionando prevemos os n ciclos admissíveis ao nível N no digrama (S-N).
Fim.
– Bibliografia:
– Robert L. Norton – Projeto de máquinas, uma abordagem integrada.
– Smith Neto - Fundamentos para o projeto de máquinas.
MUITO OBRIGADO PELA ATENÇÃO!