Criptografia de Chave Pública

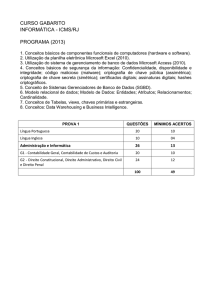
Criptografia de Chave Pública
O Problema
da Distribuição de Chaves
1
Problema da Distribuição de Chaves
 A criptografia de chave simétrica pode manter
seguros seus segredos (chave e informação),
mas se precisar compartilhar informações
secretas com outras pessoas deve-se também
compartilhar as chaves que são secretas.
 Como duas ou mais pessoas podem, de
maneira segura, enviar as chaves por meio de
linhas inseguras ?
Abril de 2006
Criptografia de Chave Pública
2
Compartilhando chaves antecipadamente
Abril de 2006
Criptografia de Chave Pública
3
Problemas com esse esquema
Abril de 2006
Criptografia de Chave Pública
4
Utilizando um terceiro confiável
Abril de 2006
Criptografia de Chave Pública
5
Problemas com esse esquema
Abril de 2006
Criptografia de Chave Pública
6
Criptografia de Chave Pública
Na criptografia simétrica, a mesma
chave é usada para encriptar e decriptar.
Na criptografia assimétrica a chave
utilizada para encriptar não é usada para
decriptar.
As chaves são significativamente
diferentes: (Ke, Kd)
Abril de 2006
Criptografia de Chave Pública
7
Criptografia de Chave Pública
 Elas são parceiras. Estão relacionadas entre si:
Kd => Ke
Ke ? =>? Kd
 O relacionamento é matemático; o que uma
chave encripta a outra decripta:
C = E(ke, P)
D(Kd, C) = P
 É possível criar uma algoritmo criptográfico
no qual uma chave encripta (Ke) e uma outra
decripta (Kd):
D( Kd, E(ke, P) ) = P
Abril de 2006
Criptografia de Chave Pública
8
Criptografia de Chave Pública
 Se a função E(ke, P) realiza uma operação, tal
como exponenciação sobre P.
 E a função D( Kd,C) é similar, e a
exponenciação usa módulo aritmético:
 Então, pode-se provar que:
D( Kd, E(ke, P) ) = P
Abril de 2006
Criptografia de Chave Pública
9
Criptografia de Chave Pública
Porque ambas as chaves são necessárias
para cifrar e decifrar a informação, uma
delas pode se tornar pública sem pôr a
segurança em perigo.
Essa chave é conhecida como chave
pública (Ke).
E sua contraparte é chamada chave
privada (Kd).
Abril de 2006
Criptografia de Chave Pública
10
Criptografia de Chave Pública
Então, encripta-se com a chave pública e
decripta-se com a chave privada.
Apenas a chave privada parceira pode ser
usada para decriptar a informação.
A chave privada é mantida em sigilo. O
texto simples encriptado permanecerá
seguro.
Abril de 2006
Criptografia de Chave Pública
11
Criptografando com Chave Pública
Chave Pública
de Criptografia
Texto
Simples
Texto
Cifrado
Algoritmo
Encriptador
Abril de 2006
Criptografia de Chave Pública
12
Decriptografando com Chave Privada
Chave Privada
Texto
Cifrado
Texto
Simples
Algoritmo de
Decriptografia
Abril de 2006
Criptografia de Chave Pública
13
Como funciona a
criptografia simétrica
Compartilhamento de uma chave comum.
Todos têm que manter a chave comum em
segredo.
É possível ?
Abril de 2006
Criptografia de Chave Pública
14
Como funciona a
criptografia de chave pública
A criptografia de chave pública torna
possível a comunicação segura entre
pessoas, sem precisar do
compartilhamento de uma chave
comum.
Chaves públicas são distribuídas entre as
pessoas, as quais guardam em segredo
suas chaves privadas correspondentes.
Abril de 2006
Criptografia de Chave Pública
15
Como funciona a
criptografia de chave pública
Possibilitam assinar mensagens sem a
presença de uma terceira parte confiável.
Os resumos de mensagens assinados
permitem verificar com facilidade a
integridade de mensagens recebidas.
Abril de 2006
Criptografia de Chave Pública
16
Gerenciamento de chaves públicas
 Problema:
Se Alice e Bob não se conhecem um ao
outro, como eles irão obter as respectivas
chaves públicas para iniciar a comunicação
entre eles ?
 Como Alice (Bob) pode ter certeza que está
realmente obtendo a chave pública de Bob
(Alice) ?
Abril de 2006
Criptografia de Chave Pública
17
Gerenciamento de chaves públicas
A solução óbvia: Bob coloca sua chave
pública na sua página Web.
Não funciona !!!
Suponha que Alice queira se comunicar
com Bob.
Abril de 2006
Criptografia de Chave Pública
18
Gerenciamento de chaves públicas
Alice, então, precisa pesquisar a chave
pública de Bob na página dele.
Como ela fará isso?
Alice começa por digitar a URL de Bob,
em seu navegador.
Abril de 2006
Criptografia de Chave Pública
19
Gerenciamento de chaves públicas
O navegador pesquisa o endereço DNS
da página de Bob e envia ao site Web de
Bob, uma solicitação HTTP-GET.
Infelizmente, suponha que Trudy
intercepta a solicitação GET e responde a
Alice com uma página falsa, fazendo a
substituição da chave pública de Bob pela
chave pública dela.
Abril de 2006
Criptografia de Chave Pública
20
Gerenciamento de chaves públicas
Quando Alice envia sua primeira
mensagem criptografada, será com ET
(a chave pública de Trudy).
Abril de 2006
Criptografia de Chave Pública
21
Gerenciamento de chaves públicas
Abril de 2006
Criptografia de Chave Pública
22
Gerenciamento de chaves públicas
Abril de 2006
Criptografia de Chave Pública
23
Desempenho
 Para informação em grande quantidade,
Algoritmos de chave pública são lentos.
(20Kb a 200Kb) por segundo.
Muito lento para processamento de dados em
volume.
 Algoritmos de chave simétrica podem
encriptar informação em grande quantidade
bem mais rapidamente.
(10Mb, 20Mb, 50 Mb ou mais) por segundo.
Abril de 2006
Criptografia de Chave Pública
24
Desempenho
Mas, encriptar 128 bits (tamanho provável
de uma chave simétrica), não leva tanto
tempo.
Solução: usar a combinação de
criptografia de chave simétrica e de
chave pública.
Abril de 2006
Criptografia de Chave Pública
25
Envelope Digital
Processo usado para criptografar
informação em grande quantidade
utilizando a criptografia de chave
simétrica e
criptografando a chave simétrica de
sessão com um algoritmo de chave
pública.
Abril de 2006
Criptografia de Chave Pública
26
Criptografando em Envelope Digital
Chave
Simétrica de
Sessão
Criptografada
Chave
Pública
Chave
Simétrica
de Sessão
Algoritmo de
Chave
Pública
Texto
Plano
Abril de 2006
Algoritmo de
Chave
Simétrica
Criptografia de Chave Pública
Texto
Criptografado
27
Descriptografando o Envelope Digital
Chave Simétrica
de Sessão
Criptografada
Chave
Privada
Chave
Simétrica
de Sessão
Texto
Criptografado
Abril de 2006
Algoritmo
de Chave
Pública
Algoritmo de
Chave
Criptografia de Chave Pública
Simétrica
Texto
Plano
28
Vantagem do Envelope Digital
 Ao invés do segredo ser compartilhado
antecipadamente.
 Segredo compartilhado, através da chave simétrica de
sessão.
 Manter uma chave separada para cada pessoa, mas
agora é a chave pública que não precisa estar protegida.
 Não é preciso armazenar as próprias chaves públicas.
Diretórios de chaves públicas podem estar disponíveis.
Abril de 2006
Criptografia de Chave Pública
29
Questões sobre a segurança
Exemplo do email usando envelope
digital.
Pao-Chi ---> Gwen
Satomi pode interceptar o email.
Abril de 2006
Criptografia de Chave Pública
30
Quebrando um algoritmo de chave pública
Abril de 2006
Criptografia de Chave Pública
31
Notas Históricas
Abril de 2006
Criptografia de Chave Pública
32
Como funciona a criptografia de chave
pública
Abril de 2006
Criptografia de Chave Pública
33
Quem inventou a Criptografia de Chave
Pública
Abril de 2006
Criptografia de Chave Pública
34
Algoritmos mais utilizados
 Três algoritmos são mais usados para resolver o
problema da distribuição de chaves:
- DH (Diffie-Hellman, 1976)
(Stanford University)
- RSA (Rivest, Shamir, Adleman)
(M.I.T, 1978)
- Ramo da matemática (Elliptic Curve, 1985)
(Neal Koblitz-University of Washington,
Victor Miller- Watson Research Center IBM)
ECDH (Elliptic Curve Diffie-Hellman,
final anos 90)
Abril de 2006
Criptografia de Chave Pública
35
Estabelecendo uma Chave
Compartilhada
Diffie-Hellman, 1976
 Acordo de chave Diffie-Hellman
Resolve problema de distribuição de
chave simétrica, criando uma chave
compartilhada.
É preciso encriptar uma chave simétrica
de sessão para criar o envelope digital.
Abril de 2006
Criptografia de Chave Pública
36
Acordo de chave Diffie-Hellman
Usa-se para tal, a criptografia de chave
pública, para criar o envelope digital.
É utilizada a tecnologia de chave
pública para gerar a chave de sessão
simétrica.
Abril de 2006
Criptografia de Chave Pública
37
Acordo de Chave Diffie-Hellman
Alice e Bob têm que concordar sobre dois
grandes números:
- p (um número primo)
- g (um número pseudo-aleatório)
onde (p-1)/2 é também um primo e certas
condições se aplicam a g.
Abril de 2006
Criptografia de Chave Pública
38
Acordo de Diffie-Hellman
p é um número primo gerado a partir de
um PRNG, sendo verificado se é primo
pelo Teste de Fermat.
g é um número gerado por um PRNG, que
se relaciona bem com o valor de p.
Abril de 2006
Criptografia de Chave Pública
39
Acordo de Diffie-Hellman
 Estes números podem ser públicos, assim,
qualquer uma das partes pode escolher p e g e
dizer ao outro abertamente.
 Seja Alice gerar, por um PRNG, um número
grande (digamos 512 bits), chamado x. Ela
guarda x como secreto.
 Alice tem agora (p, x) que define a chave
privada em DH, como em RSA.
Abril de 2006
Criptografia de Chave Pública
40
Acordo de Diffie-Hellman
Alice calcula y = g mod p . Alice tem,
então, um expoente privado x.
x
Alice inicia o protocolo do acordo de
chave enviando a Bob uma mensagem
contendo (p, g, y) .
y é um valor transmitido, portanto, público.
Abril de 2006
Criptografia de Chave Pública
41
Acordo de Diffie-Hellman
 Bob tem agora um número grande
gx mod p (512 bits) definindo a tripla
(p, g, gx mod p) a qual é transmitida para Bob,
como a chave pública DH de Alice.
 Bob escolhe um número y secreto.
 Bob responde enviando a Alice uma mensagem
contendo (gy mod p) .
Abril de 2006
Criptografia de Chave Pública
42
Acordo de Diffie-Hellman
Alice calcula
(gy mod p)x
Bob calcula (gx mod p)y
Pela lei da aritmética modular, ambos os
cálculos resultam em gxy mod p .
Alice e Bob, agora compartilham uma
chave secreta: gxy mod p
Abril de 2006
Criptografia de Chave Pública
43
Acordo de Diffie-Hellman
Bob
escolhe y
secreto
Alice escolhe
p, g públicos
e x secreto
gx mod p
chave pública
(p, g, gx mod p)
(p,x) chave
privada
A
L
I
C
E
Abril de 2006
y
g mod p
Alice calcula
(gy mod p)x
= gxy mod p
Criptografia de Chave Pública
B
O
B
Bob calcula
(gx mod p)y
= gxy mod p
44
Acordo de Chaves Diffie-Hellman
O algoritmo não criptografa os dados.
Duas partes geram o mesmo segredo e
então utilizam para ser uma chave de
sessão para uso em um algoritmo
xy
simétrico, ou seja, g mod p) .
Este procedimento é chamado Acordo de
Chave.
Abril de 2006
Criptografia de Chave Pública
45
O acordo de Diffie-Hellman
 Dificuldade de quebra do algoritmo:
Trudy conhece g e p. Se ela pudesse descobrir
x e y, ela descobriria a chave secreta.
O problema é que dado (gx mod p) e
(gy mod p), ela não pode descobrir x nem y.
Nenhum algoritmo é conhecido para computar o
módulo de logaritmo discreto de um número
primo muito grande.
Abril de 2006
Criptografia de Chave Pública
46
O algoritmo RSA
 Baseado em alguns princípios da Teoria dos
Números.
 Sumário do algoritmo:
1. Escolher dois números primos
grandes, p e q (tipicamente maiores
que 10100).
Um PRNG escolhe p;
Teste de Fermat localiza q.
Abril de 2006
Criptografia de Chave Pública
47
O algoritmo RSA
2. Compute n = p.q donde n > 10200
Ø(n) = z = (p-1).(q-1) função de Euler
3.Escolher um número relativamente
primo a z e chamá-lo de d
(isto é, tal que d não tenha fatores primos
comuns com z).
4. Encontre e tal que e.d = 1 mod z
Abril de 2006
Criptografia de Chave Pública
48
O algoritmo RSA
5. Dividir o texto plano (considerado
como uma string de bits) em blocos,
de modo que cada mensagem do
texto plano P (bloco) caia no intervalo
0 <= P < n.
Abril de 2006
Criptografia de Chave Pública
49
O algoritmo RSA
Isto pode ser feito agrupando-se o
texto plano dentro de blocos iguais de
k bits, onde k é o maior inteiro para o
qual 2k < n. Em aplicações práticas k
varia de 512 a 1024 bits.
Abril de 2006
Criptografia de Chave Pública
50
O algoritmo RSA
6. Para encriptar um mensagem P,
compute a função E’(e,n,P) = C = Pe mod n.
Para decriptar, compute a
função D’(d,n,C) = P = Cd mod n
Pode ser provado que para todo P, essas
funções são inversas:
E’(D’(x)) = D’(E’(x)) = x
Abril de 2006
Criptografia de Chave Pública
51
O algoritmo RSA
Para encriptar precisamos de e e n.
Para decriptar precisamos de d e n.
Assim, a chave pública consiste do
par (e,n) e a chave privada do par
(d,n).
Abril de 2006
Criptografia de Chave Pública
52
Segurança do RSA
A segurança do método é baseada na
dificuldade de se fatorar números
grandes.
Se um cripto-analista puder fatorar n, ele
poderia então descobrir p e q, e destes, z.
Abril de 2006
Criptografia de Chave Pública
53
Segurança do RSA e DH
 Em Diffie-Hellman, quanto maior for n, mais tempo os
programas de computador levarão – na realidade, o
mesmo tempo que levariam para fatorar.
 O problema de fatoração e o problema de log
discreto estão relacionados. Resolvendo um deles,
ambos são resolvidos.
 De praxe, em DH, n deve ter 1024 bits. Com o RSA
encontramos dois primos de 512 bits e os multiplicamos
para obter um módulo de 1024 bits.
Abril de 2006
Criptografia de Chave Pública
54
Segurança do RSA
[Coulouris et al. 2005, p294-295]
 [Rivest et al. 1978] concluiram que fatorar um
número tão grande quanto 10200 seria tomado
mais de 4 bilhões de anos, com o melhor
algoritmo conhecido e sobre um computador
que realizasse 1 milhão de instruções por
segundo.
 Um cálculo similar para os computadores de
hoje, reduziria este tempo em torno de 1 milhão
de anos.
Abril de 2006
Criptografia de Chave Pública
55
Segurança do RSA
[Coulouris et al. 2005, p294-295]
RSA Corporation tem emitido uma série
de desafios para fatorar números de mais
de 100 dígitos decimais.
Números de até 174 dígitos decimais (576
bits) têm sido fatorados, e assim o uso do
algoritmo RSA com chaves de 512 bits é
inaceitável para muitos propósitos.
Abril de 2006
Criptografia de Chave Pública
56
Segurança do RSA
[Coulouris et al. 2005, p294-295]
RSA Corporation (que retém a patente do
algoritmo RSA) recomenda um
comprimento de chave de ao menos
768 bits (em torno de 230 dígitos
decimais), por um período de segurança
a longo-prazo de aproximadamente 20
anos.
Abril de 2006
Criptografia de Chave Pública
57
Segurança do RSA
[Coulouris et al. 2005, p294-295]
 Chaves de 1024 bits são utilizadas.
 Chaves tão grandes quanto 2048 bits são
usadas em algumas aplicações.
 Os algoritmos de fatoração usados são os
melhores disponíveis.
 Algoritmos criptográficos assimétricos que usam
multiplicação de números primos como função
de uma via estarão vulneráveis quando um
algoritmo de fatoração mais rápido for
descoberto.
Abril de 2006
Criptografia de Chave Pública
58
RSA e Envelope Digital
Pode-se usar o RSA para criptografar
dados diferentes do que uma chave de
sessão, como no processo do envelope
digital, mas o RSA não é tão rápido
quanto os algoritmos simétricos.
Abril de 2006
Criptografia de Chave Pública
59
Outros algoritmos de chave pública
(Merkle, Hellman, 1978),
Knapsack Algorithm
(Rabin, 1979)
El Gamal (1985)
Schnort (1991)
(Menezes, Vanstone, 1993)
Abril de 2006
Criptografia de Chave Pública
60
El Gamal
Abril de 2006
Criptografia de Chave Pública
61
RC4
RC4 (provavelmente o algoritmo
simétrico com cifragem de ........, mais
rápido usado hoje em dia) criptografa os
dados a uma taxa 700 vezes mais rápida
do que os 1024 bits de chave (tamanho
de chave mais comumente usado) do
RSA.
Abril de 2006
Criptografia de Chave Pública
62
RC5
RC5, uma das mais rápidas cifragem de
bloco, é aproximadamente 500 vezes
mais rápido do que RSA.
A melhor maneira de se usar RSA é criar
um envelope digital.
Abril de 2006
Criptografia de Chave Pública
63
Comparando os algoritmos
Segurança
Tamanhos de Chave
Desempenho
Tamanho de transmissão
Interoperabilidade
Abril de 2006
Criptografia de Chave Pública
64
Segurança do Algoritmo
RSA está baseado no problema da
fatoração.
Diffie-Hellman (DH) está baseado no
problema do log discreto.
ECDH (ECC) está baseado, também, no
problema do log discreto.
Não se pode afirmar, atualmente qual é o
algoritmo mais seguro
Abril de 2006
Criptografia de Chave Pública
65
Tamanho de Chave
Quanto maior a chave, maior o nível de
segurança, e consequentemente menor
é a velocidade de execução.
O algoritmo de chave pública deve
utilizar um tamanho de chave ao menos
duas vezes mais longo que o da chave
simétrica, independentemente do
desempenho, por razão de segurança.
Abril de 2006
Criptografia de Chave Pública
66
Desempenho
Diz respeito a rapidez com que o
algoritmo é executado.
O algoritmo mais adequado depende do
que é mais importante – a chave pública
ou as operações de chave privada –
para um aplicativo utilizando o algoritmo.
Abril de 2006
Criptografia de Chave Pública
67
Tamanho de transmissão
É o custo ou o tempo que o algoritmo
leva para transmitir bits através do
meio de comunicação (cabos ou ar).
Com RSA e DH, o tamanho de
transmissão é o mesmo que o tamanho de
chave.
Com o ECC, é enviado duas vezes o
tamanho de chave.
Abril de 2006
Criptografia de Chave Pública
68
Interoperabilidade
 Escolher o algoritmo que todo mundo tem.
(DES, Triple DES ou AES); (RC4 ou RC5)
podem não satisfazer interoperabilidade.
 RSA é quase onipresente e tornou-se o
padrão de fato.
 DH tem boa chance, mas não é tão
disseminado.
 Com ECC, os aplicativos conversam somente
entre si. Classes de curvas elípticas (Fp e F2)
são incompatíveis.
Abril de 2006
Criptografia de Chave Pública
69
Protegendo chaves privadas
Abril de 2006
Criptografia de Chave Pública
70
Esquemas de Recuperação de Chave
Envelope digital
Terceiro confiável
Grupo de depositários de confiança
Threshold
Abril de 2006
Criptografia de Chave Pública
71
Referências
 Performance de algoritmos criptográficos
Crypto++
Open source library of cryptographic
schemes [www.cryptopp.com]
PRB optimized
[Preneel et al. 1998]
Abril de 2006
Criptografia de Chave Pública
72
Referências
 Softwares que implementam a maioria dos
principais algoritmos criptográficos:
Impresso: [Schneier 1996]
Online: versões comerciais e freeware
[www.rsasecurity.com]
[www.cryptography.org]
[privacy.nb.ca]
[www.openssl.org]
[www.pgp.com]
[International PGP]
Abril de 2006
Criptografia de Chave Pública
73
Referências
SPKI (Simple Public-KeyInfrastructure)
Creation and management of sets of
public certificates.
RFC 2693
[Ellison et al. 1999]
Abril de 2006
Criptografia de Chave Pública
74
Abril de 2006
Criptografia de Chave Pública
75