CENTRO DE ENSINO SUPERIOR
DE CONSELHEIRO
LAFAIETE / MG
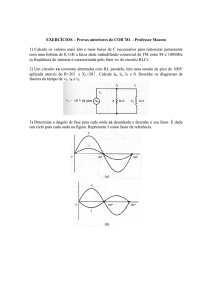
ENGENHARIA ELÉTRICA
NOTAS DE AULA
CIRCUITOS ELÉTRICOS II – 5º P
PROFESSOR : PAULO ROGÉRIO PINHEIRO NAZARETH
ALUNO(A): ....................................................................................................
2
Capítulo I – CIRCUITOS RESISTIVOS (Revisão)
I.1- CONCEITOS BÁSICOS
Todo circuito elétrico contém elementos ativos e passivos. Os elementos ativos
são as fontes de tensão e de corrente podendo estas serem independentes ou
controladas. Os elementos passivos são as resistências, as indutâncias e as
capacitâncias.
a)Fonte de tensão independente ideal.
É um elemento capaz de manter uma tensão em seus terminais independente da
corrente retirada dos mesmos.
Curva característica
Símbolo
e(t)
i(t)
e(t)
i(t)
b)Fonte de corrente independente ideal.
É um elemento capaz de manter uma corrente em seus terminais independente
da tensão terminal.
e(t)
Curva característica
Símbolo
e(t)
i(t)
i(t)
c)Fonte de tensão controlada.
É um elemento cuja tensão terminal depende de uma tensão ou corrente em
outra parte do circuito.
c.1)Fonte de tensão controlada por tensão.
eg(t)
µeg(t)
e0(t)
e0(t) = - μeg(t)
onde µ → número puro (ganho)
eg(t) → Tensão controladora
2
3
c.2)Fonte de tensão controlada por corrente.
i1(t)
e0(t)
rmi1(t)
e0(t) = rmi1(t)
onde rm → Transresistência Ω
i1(t) → Corrente controladora
d)Fonte de corrente controlada.
É um elemento cuja corrente fornecida depende de uma tensão ou corrente em
outra parte do circuito.
d.1)Fonte de corrente controlada por tensão.
i0(t)
eg(t)
i0(t) = gmeg(t)
onde gm→ Transcondutância em
siemens.
eg(t) → Tensão controladora
gmeg(t)
d.2)Fonte de corrente controlada por corrente.
i0(t)
i1(t)
i0(t) = βi1(t)
onde β → número puro (ganho)
i1(t) → Corrente controladora
βi1(t)
e)Elementos Passivos.
São elementos que recebem energia dos elementos ativos e dissipam-na na
forma de calor ou armazenam esta energia na forma de campo elétrico ou magnético.
e.1)Resistência.
Dissipa energia na forma de calor.
Símbolo
R
Curva característica
e(t)
Equação
e(t) = R.i(t)
tgα = R
α
i(t)
3
4
e.2)Capacitância.
Armazena energia na polarização do dielétrico através do campo elétrico.
Ou, explicitando a tensão vem:
Q(t ) C.e(t )
dQ (t )
de (t )
C
dt
dt
de (t )
i (t ) C
dt
t
1
1 t
.i ( )d ; de ( )
i( )d
C
C
de ( )
e( t )
1 0
1t
1t
i
(
)
d
i
(
)
d
e
(
0
)
e
(
)
i( )d
C
C0
C0
e( t )
Símbolo
C
1t
i( )d e(0)
C0
C
ou
e.3)Indutância.
Armazena energia em campo magnético.
(t ) L.i (t )
d ( t )
di (t )
L
dt
dt
di (t )
e(t ) L
dt
Ou, explicitando a corrente vem:
t
1
1 t
di ( ) e( )d ; di ( )
e( )d
L
L
i (t )
1 0
1t
1t
e( )d e( )d i (0) i () e( )d
L
L0
L0
i (t )
Símbolo
1t
e( )d i(0)
L0
L
I.2- CORRENTE, TENSÃO, POTÊNCIA e ENERGIA.
a)Corrente: É um fluxo de cargas que passam por um plano de referência na unidade
de tempo.
i (t )
dQ (t )
1C s 1 A
dt
Considere a seção de condutor dada abaixo:
i
i’
4
5
A corrente é convencionalmente positiva, se cargas positivas se movem no
mesmo sentido da seta, ou negativa em sentido contrário. Logo, i’ = - i.
b)Tensão: É a quantidade de energia fornecida ou absorvida por unidade de carga, ao
atravessar um elemento ativo ou passivo respectivamente.
i(t)
e( t )
d(t )
1J C 1V
dQ (t )
e(t)
Elemento
ativo
i(t)
e(t)
Elemento
passivo
A ponta da seta de tensão indica o potencial mais alto.
c)Potência: É a energia fornecida ou absorvida por um elemento na unidade de
tempo.
p (t )
d(t )
1 J s 1 Watt
dt
Temos que
d( t )
e( t ) d( t ) e( t )dQ( t ) , ou ainda dQ (t ) i (t )dt , logo;
dQ
d(t ) e(t ).i (t )dt
d(t )
e(t ).i (t ) , onde p(t ) e(t ).i (t )
dt
d)Energia: A energia fornecida ou absorvida por um elemento de circuito durante
um intervalo de tempo como por exemplo de t0 até t, será:
t
t
t d( ) t p( )d
0
0
t
(t ) (t 0 ) t e( ).i ( )d
0
Logo, toda energia fornecida ou absorvida, será:
t
(t) t e( ).i( )d (t 0 )
0
Aplicações:
1-No circuito abaixo, determine com que taxa a energia é dissipada para o meio
ambiente, na resistência.
40 V
4 kΩ
5
6
2-Calcule a potência dissipada na resistência do circuito abaixo.
e(t) = 10cos200t volts, para t > 0
e(t)
200Ω
3-Determine a expressão para a energia dissipada na resistência do exercício anterior,
até o instante t. Suponha t0 = 0 ; w(t0) = 0.
4-Se e(t) = 2cos10t e i(t) = 3cos10t na figura abaixo, dê uma expressão para a
potência fornecida ao elemento de circuito. Quanta energia será fornecida para o
intervalo 0 < t < 2π/10? Qual é a potência média fornecida durante este tempo?
i(t)
Elemento
de circuito
e(t)
I.3-LEIS DE KIRCHHOFF
I.3.1-Conceito de NÓ e RAMO.
NÓ → é o ponto de ligação de dois ou mais elementos.
RAMO → é qualquer elemento de dois terminais ligado entre dois NÓS.
Exemplos:
R1
R1
L
e(t)
R2
R2
R3
L
i(t)
C
C
Nº de NÓS: ----Nº de RAMOS: ----
Nº de NÓS: ---Nº de RAMOS: ----
I.3.2-Primeira Lei de Kirchhoff (Conservação da carga).
Qualquer carga que entra em um NÓ, deve deixá-lo, isto é, a soma algébrica
das correntes que chegam e que saem de um NÓ é zero.
6
7
I2
Convenção: Toda corrente que entra
no NÓ será positiva, caso contrário
negativa.
I3
N
I1
- i1 – i2 + i3 – i4 – i5 + i6 = 0
n
ij 0
j 1
I6
I4
I5
I.3.3-Segunda Lei de Kirchhoff (Conservação da energia).
A soma algébrica das tensões em qualquer percurso fechado é zero.
e1
A
Devemos notar que a energia necessária para mover
uma unidade de carga de A até B é e1, de B até C é e2,
de C até D é e3, de D até A é - e4.
Como voltamos ao ponto inicial A, a unidade de carga
deve possuir a mesma energia. Logo;
B
e2
e4
e1 + e2 + e3 – e4 = 0, ou
m
D
ek 0
C
e3
k 1
Aplicações:
1-Determine a tensão eAB no circuito dado:
A
8 kΩ
7 kΩ
e(t)=80V
5 kΩ
B
2-A parte do circuito abaixo limitada pela linha tracejada é um modelo de um
conversor de impedância negativa. Determine e1/i1.
i1(t)
i3(t)
e1(t)
i2 = 3i1(t)
2,0 k
7
8
3-Na figura abaixo, os elementos representam a indutância e a resistência da bobina
de deflexão de uma televisão. Se L = 5 H, R = 1 Ω e se a corrente tiver a forma de
onda mostrada, qual será a forma de onda da tensão?
i(t)
i(t) R
e(t)
1
L
t
0
5
6
11 12
4-Determine e1/i1 para o circuito da figura abaixo e sugira para a parte do mesmo
limitada pela linha tracejada.
i1(t)
e2(t) = 4e1(t)
R
e1(t)
5-Seja a tensão no circuito abaixo zero para t < 0 e 1 V para t > 0. Determine i(t) para
t > 0, sabendo-se que a corrente i(0) = 0.
R
e(t)
i(t)
L
I.4-RESISTÊNCIA EQUIVALENTE
I.4.1-Condição de equivalência.
Sejam os circuitos I e II abaixo:
i1
e1
I
i2
e2
II
O circuito I é equivalente ao circuito II e vice-versa se e somente se
e1 e 2 i1 i 2 .
* Revisar associação de resistências, indutâncias e capacitâncias.
8
9
I.4.2-Divisores de tensão e corrente.
a)Divisor de tensão.
R1
R2
i(t)
e k R k .i (t ) ; i (t )
ek
e(t)
Rk
Logo , e k
e(t )
R eq
Rk
.e(t )
R eq
Rn
b)Divisor de corrente.
ik
ik
i(t)
R1
e(t)
R2
Rk
Rn
e(t )
; e(t ) Re q.i (t )
Rk
Logo , i k
R eq
Rk
.i (t )
Exercícios de aplicação.
1-Determine a resistência vista pela fonte e a potência fornecida pela mesma.
2Ω
1Ω
3Ω
e(t)
6Ω
4Ω
12Ω
2-Determine as tensões nas resistências R1 e R2.
R1
Dados: R1 = 20 KΩ e R2 = 30 KΩ,
e1
e2
e(t)
R2
e(t) = 120 volts
3-Determine as correntes i1 e i2 no circuito abaixo:
10 mA
i2
i1
30k
20k
9
10
I.4.3-Resistência equivalente de circuitos contendo fontes controladas.
Circuitos contendo fontes controladas e resistências podem ser substituídas por
uma única resistência, podendo esta ser positiva ou negativa. Para se determinar a
resistência equivalente de um circuito nessas condições, só existe um meio, que
consiste em alimentar os terminais externos com uma fonte independente, o que fará
circular uma corrente, que é inversamente proporcional à resistência equivalente.
Tomando-se o quociente
e APLIC ADA
R e q , obtemos o resultado desejado.
i ABSO RVIDA
Exercícios de aplicação.
1-Determine a resistência equivalente do circuito abaixo:
1
i 1 (t )
3
A
i1(t)
6Ω
B
2-Determine a resistência equivalente do circuito abaixo:
rp
A
µeg
eg
Rk
B
I.5-LINEARIDADE.
I.5.1-Efeito da multiplicação da entrada por um fator.
Pela definição de linearidade, se multiplicar a entrada por um fator K a saída
também será multiplicada por esse mesmo fator. Poderemos então utilizar essa lei na
análise de circuitos.
10
11
I.5.2-Teorema da Superposição.
Se um circuito linear for excitado por duas ou mais fontes independentes, a
resposta total será a soma das respostas a cada fonte individual, com as demais em
repouso.
-Fonte de tensão em repouso → Curto-circuito → e = 0.
-Fonte de corrente em repouso → Circuito aberto → i = 0.
Obs.: Matar uma fonte significa coloca-la em repouso.
Exercícios de aplicação.
1-Determinar e0 quando e1 = 5 v no circuito abaixo, calculando inicialmente a tensão
necessária na fonte para produzir uma saída e’0 = 3 v.
2kΩ
1kΩ
2kΩ
e1
3kΩ
e0
2-Determine a tensão e2, usando superposição.
320Ω
e2
e1=16v
680Ω
i1 = 20mA
3-Determine a tensão e0, usando superposição.
1Ω
3A
8V
6Ω
5Ω
e0
3Ω
4-Determine a tensão e2 no circuito abaixo, usando superposição.
3Ω
i1
12V
4Ω 2i1
e2
3A
11
12
I.6-TEOREMAS DE THÈVENIN E NORTON.
I.6.1-Introdução.
Qualquer circuito de dois terminais externos, que possua internamente apenas
resistências e fontes controladas é equivalente a uma única resistência. Entretanto, se
circuitos possuírem além das resistências e fontes controladas, as fontes
independentes, os circuitos não poderão ser equivalentes a uma única resistência,
porque fontes independentes não são elementos lineares.
I.6.2-Teorema de Thévenin.
Qualquer circuito de dois terminais externos e que contenha resistências, fontes
controladas e fontes independentes, pode ser substituído por uma única resistência em
série com uma fonte de tensão, para efeitos externos.
RTH
A
A
N
eoc
B
B
Sendo: eoc → Tensão entre os terminais A e B.
oc → open circuit
RTH → Resistência medida entre os pontos A e B com as fontes
independentes em repouso.
Exemplo1: Determine o circuito equivalente de Thévenin do circuito de dois
terminais abaixo.
10kΩ
A
30V
5kΩ
B
Exemplo2: Use o Teorema de Thévenin para determinar e0.
2kΩ
5V
1kΩ
2kΩ
3kΩ
e0
12
13
I.6.3-Teorema de Norton.
Qualquer circuito que contenha resistências, fontes controladas e fontes
independentes, pode ser substituído por uma única resistência em paralelo com uma
fonte de corrente, para efeitos externos.
A
A
N
isc
RN
B
B
Onde: A resistência é a resistência equivalente vista dos terminais externos A e B
abertos com as fontes independentes em repouso. (RN)
O valor da fonte de corrente tem o valor da corrente obtida com os terminais
externos curto-circuitados.
isc → i short circuit
Obs.: RTH = RN
Exemplo1: Substitua tudo, exceto a resistência de 680 Ω por um circuito equivalente
de Norton, e então calcule e2.
320Ω
e2
e1=16v
680Ω
i1 = 20mA
Exemplo2: Determine e0 no circuito abaixo aplicando o Teorema de Norton na parte
limitada pela linha tracejada.
20i1
i1
3kΩ
6V
2kΩ
10kΩ
e0
13
14
I.6.4-Relação entre Thévenin e Norton.
Suponha o circuito a seguir, onde temos o seu Thévenin equivalente:
RTH
A
A
1
eoc
2
B
B
Se
2
é o Thévenin equivalente ao
equivalente do circuito
1 através do
1 , então podemos determinar o Norton
2 ;
Req
A
eoc
i sc
isc
e oc
Req
B
Req
A
R N Re q
B
A
Req
Norton equivalente → isc
B
I.7-EQUAÇÕES NODAIS.
Suponha que entre os nós mostrados na figura abaixo estejam ligados um certo
número de ramos (não desenhados). As tensões mostradas pelas setas cheias são as
tensões de cada nó em relação ao nó R chamado referência. As setas pontilhadas
mostram a d.d.p. entre dois nós quaisquer menos o de referência.
A
eA - eB
B
eB – eC
C
a)
eC – eR
eA – eR
R
14
15
Se ao nó R atribuirmos o valor zero, poderemos escrever:
A
eA - eB
eB – eC
B
C
Obs.: O símbolo de terra ligado ao nó
R significa que arbitramos o seu
potencial zero.
b)
R
As duas figuras anterioresa) e b) são equivalentes, mas devido ao maior
emprego da b) iremos também utiliza-la. As tensões eA ; eB e eC são chamadas
tensões dos nós. A tensão em qualquer ramo do circuito é dada pela diferença das
tensões dos nós a ele ligados. Estas tensões (ddp) não são geralmente mostradas no
circuito.
A corrente através de qualquer ramo resistivo é dada por i e
R
, onde e é a
ddp entre os terminais do ramo.
Se as únicas fontes forem fontes de corrente independentes, as correntes nos
ramos podem ser expressas em função das N – 1 tensões de nós, onde N é o número
de nós, obtendo N – 1 equações independentes que podem ser resolvidas para
determinar as tensões dos nós.
Obs.: Aos nós que estiverem ligados a fontes independentes de tensão não será
necessário aplicar a 1ª Lei de Kirchhoff nos mesmos porque suas tensões já são
conhecidas.
Exercícios de aplicação.
1-Determine a tensão nos terminais e a potência fornecida por cada fonte de corrente
no circuito abaixo.
2kΩ
5 mA
4kΩ
2 mA
3kΩ
6kΩ
2-Determine a tensão e0 no circuito abaixo:
i3=5.10-3e2
e2
1k
4 mA
2k
9k
e0
15
16
3-Determine e4 no circuito abaixo e a resistência total vista pela fonte de tensão.
1k
4k
e4
6V
1k
2k
4-Determine
2k
e2 e0
e
no circuito abaixo que é um modelo para dois amplificadores a
e1
e1
válvula idênticos com resistência comum de catodo.
R0
R0
rp
rp
e0
µeg1 µeg2
eg1
e1
eg2
Rk
e2
I.8-EQUAÇÕES DE LAÇOS.
Este é um outro método sistemático utilizado na análise de circuitos. Neste
método, é mais conveniente tratar cada elemento como um ramo separado, exceto as
resistências em série e paralelo que devem ser combinadas em ramos simples.
Um circuito contendo B ramos e N nós, todas as correntes podem ser expressas
em função de L = B – N + 1 correntes independentes pelo método das correntes de
Kirchhoff. Se a tensão em cada ramo resistivo é dada por e = R.i, e se todas as fontes
forem fontes de tensão independentes, então todas as tensões desconhecidas poderão
ser expressas em função das L correntes independentes. A Lei das tensões de
16
17
Kirchhoff dará então L equações independentes, que poderão ser resolvidas
simultaneamente para determinar as correntes desconhecidas.
Exercícios de aplicação.
1-Dado o circuito abaixo determine todas as correntes.
3Ω
4Ω
24 V
6Ω
60 V
2Ω
2-Determine a tensão e4 na figura abaixo.
1k
4k
e4
6V
1k
2k
2k
I.9-CIRCUITOS DUAIS
Dois circuitos são ditos duais quando o sistema de equações que descreve um
deles for idêntico ao sistema de equações que descreve o outro exceto pela troca de
símbolos. Portanto, logo que um deles seja resolvido, a solução do outro pode ser
imediatamente escrita.
Exercícios de aplicação.
1-Escreva as equações de laço da figura I e as equações nodais da figura II.
Fig. I
2Ω
e1
i1
Fig. II
e1 4S
6Ω
4Ω
i2
e2
i1
2S
e2
6S
i2
17
18
6i1 4i 2 e1
4i1 10i 2 e 2
6e1 4e 2 i1
4e1 10e 2 i 2
Obs.: Podemos notar que os dois sistemas são idênticos exceto pela troca de
símbolos. Sempre que as equações de laço de circuito forem iguais às equações
nodais do outro, exceto pela troca das correntes pelas tensões, estes circuitos são ditos
duais.
Para construir o dual de um circuito dado, podemos substituir e por i e viceversa e então desenhar um circuito que corresponda às novas equações.
2-Construa o dual do circuito abaixo:
4F
e( t ) e C e R e L
eC
e(t)
i(t) eR
2H
3Ω
1
di
e(t ) idt 3i 2
4
dt
eL
Fazendo a troca de símbolos, fica:
1
de
i(t) edt 3e 2
4
dt
i(t)
4H
3S
2F
Conclusão: Pelos exercícios anteriores, podemos notar que ao se construir o dual, o
que era série passa a ser paralelo, fonte de tensão passa a ser fonte de corrente,
capacitância passa para indutância, resistência passa para condutância, etc , segundo
tabela abaixo:
QUANTIDADES
DUAIS
Tensão
Corrente
Laço
Nó
Capacitância
Indutância
Série
Paralelo
Circuito aberto
Curto-circuito
Resistência
Condutância
18
19
I.10-TRANSFERÊNCIA MÁXIMA DE POTÊNCIA.
Algumas vezes, na análise de circuitos, estamos interessados em determinar a
máxima potência que pode ser fornecida a uma carga. Ao usar o teorema de
Thévenin, podemos determinar a potência máxima que um circuito consegue fornecer
e o modo como ajustar a carga para efetuar uma transferência máxima de potência.
Considere o circuito abaixo;
R
i
VRL
V
2
Pc arga
RL (Carga)
2
V
VRL
.R L
i .R
RL
R RL
2
2
Pc arga
dP
V
.R L , vamos fazer c arga 0 , onde teremos :
dR L
R RL
dPc arga
dR L
2
V
[R R L .0 V 2 .2R R L ].R L
R
R
R R L 4
L
2
R R L 2 .V 2 2V 2 R R L .R L
0
R R L 4
R RL 0
; V 2 R R L .[R R L 2R L ] 0
RL R
Conclusão: Para que haja a máxima transferência de potência para a carga, é
necessário que a resistência da carga seja igual à resistência equivalente do circuito.
Exemplo de aplicação.
Para cada rede abaixo, determine RL para transferência máxima de potência e a
potência máxima dissipada pela carga.
4Ω
2Ω
2Ω
12V
2A
RL
2A
3Ω
12V
6Ω
RL
19
20
Capítulo II – CIRCUITOS COM CAPACITÂNCIA E INDUTÂNCIA
-Resposta livre e completa de circuitos de 1ª ordemII.1- INTRODUÇÃO
Foi trabalhada até o momento, a análise de circuitos elétricos que continham
fontes independentes, fontes controladas e apenas resistores.
Introduziremos agora, dois elementos adicionais, ou seja, o capacitor e o
indutor. Estes elementos são lineares, porém ao contrário do resistor, suas
características terminais são descritas por equações diferenciais lineares. Outra
característica particular desses novos componentes é a sua capacidade de absorver
energia do circuito, armazena-la temporariamente e, mais tarde devolve-la.
Em geral, as formas de onda da entrada e da saída não serão semelhantes e a
resposta em um instante t0 dependerá dos valores de entrada pata todo t ≤ t0.
As funções de entrada a serem consideradas são mostradas a seguir e são
chamadas de funções singulares.
Função Degrau
x(t)
0
Função Impulso
Função Rampa
x(t)
t
0
x(t)
t
0
t
II.2- RESPOSTA LIVRE E AO DEGRAU
Os circuitos aqui apresentados podem ser descritos por meio de uma única
equação diferencial, para todos os valores de “t” maiores que um certo instante de
referência, tomado como t = 0.
O resultado à uma entrada para todo t > 0, será uma expressão também para
t > 0, que contem uma constante de integração. Esta constante poderá ser calculada,
se o valor da tensão nos terminais da capacitância ou o da corrente passando pela
indutância for conhecido em t = 0+.
É importante saber que, se todas as tensões e correntes permanecerem finitas, a
tensão nos terminais de uma capacitância e a corrente passando por uma indutância
não poderão se alterar instantaneamente.
Portanto, podemos dizer que os valores destas grandezas e c(t) e iL(t) são os
mesmos em t = 0+ e t = 0-.
20
21
Exemplo 1
Considere o circuito R-L série a seguir com uma fonte externa. Para t < 0, a chave K
está aberta, e i(t) = 0. A chave se fecha em t = 0, e deseja-se obter i(t) para t > 0. Para
t < 0, e(t) = 0 e para t > 0, e(t) = 1 V. Dados: i(0-) = i(0+) = 0.
K
L
i(t)
R
e(t)
Exemplo 2
Para t < 0, a chave K do circuito R-C dado está na posição inferior e e(t) = 0. Em t =
0, a chave é levada `a posição superior de maneira que i(t) tem a forma de onda dada.
Determine e esboce e(t).
i(t)
i(t)
K
R
i1(t) = 1A
C
1A
e(t)
t
0
Exemplo 3
Suponha que em algum instante no passado, uma carga tenha sido colocada na
capacitância do circuito abaixo, de maneira que e(0-) = A volts. Se a chave K se fecha
em t = 0, determine e esboce e(t).
K
R
C
e(t)
II.3- FUNÇÕES SINGULARES
II.3.1- Função Degrau Unitário => U-1(t)
U-1(t)
0, para t 0
U 1 ( t )
1, para t 0
1
t
0
21
22
Se substituirmos “t” por “(t – a)”, a curva se deslocará “a” unidades para a
direita;
U-1(t - a)
0, para t a
U 1 ( t a )
1, para t a
1
t
a
0
Uma função degrau de valor A, será:
A.U-1(t - a)
0, para t a
A.U 1 ( t a )
A, para t a
A
t
a
0
Nota: Podemos obter um número infinito de funções a partir da função “Degrau” por
integrações e derivações sucessivas.
II.3.2- Função Rampa Unitária => U-2(t)
t
t
d
U
(
t
)
U
(
t
)
; U 3 (t ) U 2 ( )d
U 2 ( t ) U 1 ( )d ;
2
1
dt
U-2(t)
U-3(t)
Inclinação = 1
t
t
0
0
Obs.: Todas as funções singulares são relacionadas por:
t
U n 1 ( t ) U n ( )d ; U n 1 t
d
U n (t)
dt
II.3.3- Função Impulso => U0(t)
U 0 (t)
d
U 1 ( t ) 0 , para t ≠ 0.
dt
Sejam as figuras:
f-1(t)
f0(t)
1/Δ
1
0
Δ
t
0
Δ
t
22
23
f-1 é uma aproximação de U-1(t) quando Δ é pequeno, onde:
f 0 (t )
t
d
f 1 ( t ) f 1 ( t ) f 0 ( )d
dt
Observe que a área sob f0(t) é sempre unitária independente do valor de Δ.
lim f 1 (t ) U 1 (t ) ; lim f 0 (t ) U 0 (t ) de área 1.
0
0
Logo, U0(t) será chamada de Impulso Unitário.
U0(t - a)
U0(t)
AU0(t - a)
∞
∞
1
∞
1
t
0
0
a
A
t
0
a
t
II.4- Resposta às funções singulares.
Sabe-se que,
iC
de
1
; W ( t ) Ce 2
dt
2
eL
di
dt
; W(t )
1 2
Li
2
II.4.1- Teorema 1 => Se todas as tensões e correntes permanecerem finitas, a tensão
nos terminais de capacitância e a corrente passando por uma indutância, não poderão
alterar instantaneamente.
- Admita que a tensão de uma capacitância se altere instantaneamente, de
maneira que exista um degrau na curva de e(t) em função de “t”.
Assim,
de
e, portanto a corrente i(t) deve conter um impulso, e dessa forma ela não
dt
permanecerá finita.
Uma alteração instantânea de e(t) corresponde a uma alteração instantânea na energia
armazenada, W pdt , o que requer um fluxo de potência infinito e, portanto uma
corrente infinita.
Logo, para uma indutância seria necessária uma tensão infinita para alterar
instantaneamente a corrente passando por ela.
23
24
II.4.2- Teorema 2 =>
Um impulso unitário de corrente entrando em uma
capacitância altera sua tensão instantaneamente de 1/C volts, enquanto que um
impulso unitário de tensão aplicado aos terminais de uma indutância, altera a corrente
que passa por ela de 1/L ampères.
e(t )
1 t
1
U 0 ( )d U 1 (t ) Volts
C
C
i( t )
1 t
1
U 0 ( )d U 1 ( t ) Ampères
L
L
2
1 1
1
Wc C
Joules
2 C
2C
2
1 1
1
; WL L
Joules
2 L
2L
Logo, uma energia de 1 2C joules colocada instantaneamente no campo elétrico de
uma capacitância, altera sua tensão de 0 para 1 C volts.
Uma energia de 12L joules colocada instantaneamente no campo magnético de uma
indutância, a corrente é alterada de 0 para 1 L ampères.
II.4.3- Teorema 3 => A tensão nos terminais de uma capacitância e a corrente que
passa em uma indutância devem sempre permanecerem finitas.
Exemplo 1 => Determine as respostas ao degrau e ao impulso do circuito
representado na figura:
r(t) → Resposta ao degrau
R
e(t)
C
i1(t)
h(t) → Resposta ao impulso
Exemplo 2 => Determine as respostas ao degrau e ao impulso unitário do circuito
abaixo:
R
i(t)
r(t) → Resposta ao degrau
e(t)
C
h(t) → Resposta ao impulso
24
25
Exemplo 3 => Determine as respostas ao degrau e ao impulso unitário do circuito
abaixo:
L
i(t)
r(t) → Resposta ao degrau
R
e(t)
h(t) → Resposta ao impulso
Exemplo 4 => Determine as respostas ao degrau e ao impulso unitário do circuito a
seguir:
r(t) → Resposta ao degrau
R
L
i(t)
e(t)
h(t) → Resposta ao impulso
II.5- Aplicações.
II.5.1- Determine e esboce as respostas ao degrau e ao impulso do circuito para obter
e0(t):
R1
r(t) → Resposta ao degrau
R2
e1(t)
C
e0(t)
h(t) → Resposta ao impulso
II.5.2- Determine a resposta ao degrau unitário do circuito abaixo usando o teorema
de Norton, para obter e0(t):
R1=1Ω
e1(t)
C2=2F
R3=3Ω
C4=4F
e0(t)
25
26
Capítulo III – SOLUÇÃO CLÁSSICA DE CIRCUITOS UTILIZANDO
EQUAÇÕES DIFERENCIAIS.
III.1- Introdução.
Qualquer circuito linear e invariante no tempo podem ser descrito por uma
equação diferencial com coeficientes constantes que relaciona a entrada e a saída.
x(t) CIRCUITO
an
dn y
dt n
a n 1
d n 1 y
dt n 1
y saída
onde
x entrada
y(t)
dy
dmx
d m1 x
dx
... a 1
a 0 y b m m b m 1 m1 ... b1
b0x
dt
dt
dt
dt
a n , b m coeficient es constantes (números) que dependem do circuito.
Como x(t) é a entrada que é geralmente conhecida, podemos derivá-la “m”
vezes e todo o lado direito tornar-se-á uma função do tempo conhecida como
“função forçante” F(t). Logo, a equação diferencial geral se reduzirá para:
an
dn y
dt n
a n 1
d n 1 y
dt n 1
... a 1
dy
a 0 y F( t )
dt
Observações:
a) Se F(t) for nula, a equação se reduz a:
an
dn y
dt n
a n 1
d n 1 y
dt n 1
... a 1
dy
a0y 0,
dt
denominada
Equação
Diferencial
Homogenia de n-ésima Ordem.
b) Se F(t) ≠ 0, a equação denomina-se Equação Diferencial Não Homogenia de
n-ésima Ordem.
Portanto, a solução geral será y(t) = yH(t) + yP(t)
Onde
yH(t) → solução complementar ou homogenia;
yP(t) → solução particular
III.2- Solução da Equação Diferencial Homogênia.
Seja a equação, a n
dn y
dt n
a n 1
d n 1 y
dt n 1
... a 1
dy
a 0 y 0 , que admitirá n
dt
soluções.
26
27
Admita que as soluções da equação anterior tenham a forma y( t ) .
rt
Substituindo na equação, teremos:
a n r n rt a n 1r n 1 rt ... a 1r rt a 0 rt 0
rt a n r n a n 1r n 1 ... a 1r a 0 0
onde tem se a n r n a n 1r n 1 ... a 1r a 0 0
Esta última equação é chamada de equação característica ou auxiliar. As
raízes desta equação serão denotadas por r1 , r2 ,..., rn ; onde as soluções da equação
diferencial tornam-se:
y1 r1t ; y 2 r2 t ; ...; y n rn t
Se todas as raízes r1, r2,..., rn forem distintas, as n soluções serão independentes e a
solução da equação diferencial será:
y H (t ) k1 r1t k 2 r2t ... k n rn t
Observações:
a) Se algumas raízes forem complexas elas devem aparecer aos pares
conjugados e a solução será escrita de outra forma:
r1 j
Sejam as duas raízes
, então;
r
j
2
y H ( t ) K1 j t K 2 j t
y H ( t ) K1 t jt K 2 t jt t K1 jt K 2 jt
Pela fórmula de Euler => j cos jsen , vem:
y H ( t ) t K1 cos t jsen t K 2 cos t jsen t
y H ( t ) t K1 K 2 cos t jK1 K 2 sen t
K1 e K 2 devem ser complexos conjugados, logo;
K1 K 2 K 3
; K1 K 2 jK 4
y H ( t ) t K 3 cos t jjK 4sen t ; sendo jjK 4 K 5 , teremos:
y H ( t ) t K 3 cos t K 5sen t
27
28
Multiplicando-se e dividindo-se a expressão anterior por K K3 K5 ,
2
2
K
K5
Φ
K3
y H ( t ) K
t
K3
K 32 K 5 2
cos t
K5
K 32 K 52
sen t
y H ( t ) K t cos cos t sensen t
y H ( t ) K t cos t
b) Se houver raízes repetidas r1 = r2, teremos que a solução homogenia será:
y H (t ) K1 K 2 t r1t
Se a raiz for repetida K vezes, r1 r2 ... rk , vem:
y H (t ) K1 K 2 t K 3 t 2 ... K k t k 1 r1t
III.3- Solução da Equação Diferencial Não Homogênia.
Consta de duas partes:
1ª- Fazendo-se F(t) = 0 na equação diferencial não homogenia, obtemos a solução
homogenia correspondente chamada de “Solução Complementar” yH(t).
2ª- A “Solução Particular” yP(t), que é obtida pelo método dos coeficientes
indeterminados, consiste em examinar a função forçante F(t) e estimar a forma de
yP(t). Esta forma é uma combinação linear dos termos de F(t) e suas derivadas. A
forma estimada de yP(t) é levada na equação diferencial determinando-se as
constantes.
Forma estimada de yP(t)
At n
B coswt
k n t n k n 1t n 1 ... k1t k 0
k1 cos wt k 2senwt
Csenwt
k1 cos wt k 2senwt
D t
t cos wt
Onde k1 ; k2 ;...; kn ;
k0 ; A ; B ; C ; D são
constantes.
k t
k1 t cos wt k 2 t senwt
28
29
Obs.: Sempre que um termo de F(t) corresponder a uma raiz repetida da equação
característica como, por exemplo, uma raiz repetida “m” vezes, ao estimar-se a forma
da solução particular, o termo correspondente a essa raiz deverá ser multiplicado por
tm.
III.4- Condições iniciais ou de contorno.
III.4.1- Introdução.
Para obter-se as constantes da solução particular yP(t), basta substituir a
solução estimada na equação diferencial. Para obter-se as constantes da solução geral
y(t) = yH(t) + yP(t) , necessitamos de certas condições iniciais, ou seja:
dy
d2y
d n 1 y
y (0 ) ;
;
;...; n 1
dt 0 dt 2
dt
0
0
dy
dy(0 )
Obs.: Não confundir
com
0 y(0 ) é cons tan te
dt 0
dt
III.4.2- Obtenção das condições iniciais.
a)Obtenção de y(0+) => se não houver impulsos de corrente ou tensão no
circuito, a tensão nos terminais de uma capacitância ou a corrente em uma indutância
não poderão alterar instantaneamente.
e c (0 ) e c (0 ) ; i L (0 ) i L (0 )
b)Se houver impulsos de corrente em uma capacitância e impulsos de tensão
em uma indutância, a tensão na capacitância altera-se instantaneamente para 1/C
volts e a corrente na indutância de 1/L Ampéres.
c)Obtenção de
dy
=> essa grandeza pode ser geralmente obtida através das
dt 0
leis dos elementos:
dec ( t )
i c (0 ) diL ( t )
e L (0 )
;
dt 0
C
dt 0
L
29
30
Nota: Por outras vezes essas derivadas devem ser obtidas por métodos indiretos e
até por meios engenhosos.
Exemplos.
Exemplo 1 => Determine a solução geral da seguinte equação diferencial:
d2y
dt
2
2
dy
w 0 2 y 0 [ E. D. homogenia ]
dt
Exemplo 2 => Resolver a E. D. C
a)i1(t) = 1 A
de0 1
e 0 i1 , para e0(t) quando:
dt R
b)i1(t) = coswt
de0
3e 0 t cos t .
dt
Exemplo 3 => Determine a solução geral de
Exemplo 4 => Resolva a E. D. L
d 2i
dt 2
2R
Exemplo 5 => Determine a solução de
Exemplo 6 => Resolver a E. D.
d2y
dt 2
2
dy
5y t .
dt
dy
2y 2t .
dt
d2y
Exemplo 7 => Resolva a E. D.
di 1
1
L
i , quando R 2 .
dt C C
C
dt 2
4
dy
4y 2t .
dt
Exemplo 8 => Se o circuito abaixo não contiver energia armazenada para t < 0,
determine os valores de e0 (t ) e
i(t)=U-1(t)
R1
de0 (t )
em t = 0+.
dt
R2
C
e0(t)
L
Exemplo 9 => Determine e 0 ( t ) e
de0 ( t )
em t = 0+, não havendo energia
dt
inicialmente armazenada no circuito abaixo.
C4=4F
e1(t)=(6cos2t)U-1(t)
C2=2F
2Ω
3Ω
e0(t)
30
31
Exemplo 10 => Determine os valores de e 4 ( t ) ,
de (t )
de4 ( t )
em t = 0+, se
, e0 (t ) , 0
dt
dt
o circuito a seguir não contiver nenhuma energia inicialmente armazenada.
i3(t)=3e1(t)
i0(t)
1Ω i2(t) 1/2F
i1(t)
i(t)=U-1(t)
2Ω
2Ω
e1(t) e2(t)
e4(t)
e0(t)
ec(t)
2H
eL(t)
III.5- A solução completa de circuitos
Roteiro para sua obtenção:
1- Determina-se uma equação diferencial relacionando-se a entrada e a saída.
Se aparecerem integrais, a equação deve ser diferenciada termo a termo até
que se exclua o sinal de integração.
2- Resolve-se a equação diferencial determinando-se a solução complementar,
a particular e a geral.
3- Determinam-se as condições iniciais, que serão tantas quantas for o grau da
equação diferencial.
4- Com as condições iniciais determinam-se as constantes da solução geral,
escrevendo-se a mesma que é a saída desejada.
III.5.1- Exemplos
Exemplo 1 => Se a capacitância no circuito da figura estiver descarregada para t < 0,
determine e0(t) para t > 0 quando i1(t) = U-1(t) A e quando i1(t) = (coswt)U-1(t) A.
i1(t)
C
R
e0(t)
Exemplo 2 => O circuito da figura não contem energia armazenada para t < 0. Se
R2=L/C e i1(t) = U-1(t), determine i0(t), ic(t) e e1(t).
31
32
ic(t)
R
i0(t)
R
e1(t)
i(t)
C
L
III.6- O significado físico das soluções complementar e particular.
III.6.1- Introdução
A solução complementar YH(t) é a solução da equação diferencial, estando a
entrada e, portanto a função forçante F(t) feita igual a zero. A forma de YH(t) é
completamente determinada pelas raízes da equação característica que depende
somente do circuito. Como a solução complementar representa o comportamento do
circuito quando a fonte estiver em repouso, ele é chamada “resposta livre”. A
solução particular YP(t) é chamada de “resposta forçada”.
YH(t) => Entrada nula, F(t) = 0 → Equação característica depende do circuito
→ Constantes K1, K2, ... , Kn dependem de alguma energia previamente armazenada
ou impulso em t = 0 → Chama Resposta Livre.
YP(t) => Estimada pela F(t) → Constantes dependentes de F(t) → Independe
de energia armazenada → Resposta Forçada.
III.6.2- Natureza da resposta livre
Pode ser estudada, examinando-se as raízes da equação característica, que
podem ser desenhadas num plano complexo.
Sejam r1 e r2 as raízes:
a) Se r1 = -α1 e r2 = -α2 => Duas raízes reais distintas.
I
-α1
Significa duas exponenciais decrescentes.
-α2
R
r1
r2
YH (t ) K1 1t K 2 2 t
32
33
b) Se r1 = -α1 e r2 = 0
I
-α1
R
r2
r1
Significa uma exponencial decrescente e
uma constante.
YH (t ) K1 1t K 2
c) Se r1 = -α1 e r2 = -α2 e α1 = α2
I
-α1= -α2
Significa uma exponencial decrescente.
R
r1= r2
YH (t ) (K1 K 2 t ) 1t
d) Se r1 = -α1 + jβ1 e r2 = -α1 - jβ1 => Duas raízes complexas conjugadas.
r1
I
-α1
Significa uma oscilação amortecida.
β1
R
-β1 -α1
YH (t ) K1 1t cos(t )
r2
e) Se r1 = + jβ1 e r2 = - jβ1 => Duas raízes imaginárias conjugadas.
I
r1
Significa uma oscilação constante.
β1
R
-β1
YH ( t ) K1 cos( t )
r2
f) Se r1 = α1 + jβ1 e r2 = α1 - jβ1 => Duas raízes complexas conjugadas.
I
α1
r1
Significa uma oscilação crescente.
β1
R
α1
-β1
YH (t ) K1 1t cos(t )
r2
33
34
g) Se r1 = α1 e r2 = α2 => Duas raízes reais distintas positivas.
I
α2
Significa exponenciais crescentes.
α1
r1
r2
R
YH (t ) K1 1t K 2 2 t
Conclusões:
1ª-Toda raiz da equação característica que estiver situada no semi-plano esquerdo
aberto conterá uma resposta livre que tende a zero quando t→∞ significando circuito
estável, como indicado nas letras a até d.
2a-Raízes conjugadas no eixo imaginário, circuito estável. A resposta não tende a
zero, mas também não cresce. (e)
3ª-Raízes no semi-plano direito aberto conterá uma resposta livre que tende a infinito.
Circuito é instável. Letras f e g.
Obs.: Em certas aplicações em comunicações e em sistemas de controle, é necessário
que se conheça a maneira como essas raízes se movem no plano complexo, à medida
que um dos elementos é variado.
Exemplo: Esboce o lugar geométrico gerado pelas raízes da equação característica
quando a resistência “R” é variada de zero a ∞.
C
R
e(t)
i (t)
L
34
35
III.7- O Estado Permanente Em Corrente Contínua Pura.
Uma fonte que é igual a uma constante para todos os valores de “t” é chamada
fonte de corrente contínua pura. Portanto, uma função degrau é equivalente a uma
fonte de CC pura aplicada subitamente ao circuito. Nesta seção nos interessa a
resposta em estado permanente de maneira que consideraremos que o componente
transitório já tenha desaparecido. Se o estado permanente é a resposta forçada, sua
forma depende da entrada e se esta é uma constante, as respostas em estado
permanente serão constantes. Como a derivada de uma constante é zero, vem:
ic C
dec
di
0 e e L L L 0.
dt
dt
Logo, a capacitância pode ser substituída por um circuito aberto e a indutância
por um curto-circuito.
Exemplos:
1º-No circuito abaixo, a chave K se fechou a tempo suficiente para que todo
transitório tenha desaparecido. Determine e0(t) em estado permanente, e as energias
armazenadas nas indutâncias e capacitâncias.
K
L1
4k
2k
2 mH
2k
1k
C2
6V
C1
1μF
4 mH
L2
1μF
e0(t)
2º-A chave K do circuito abaixo esteve fechada durante um intervalo de tempo
suficiente para que quaisquer transitórios tenham desaparecido. Se K é reaberta em
t=0, determine a tensão nos terminais da chave para t = 0+ e para t > 0.
eK
10 V
2Ω
2H
3Ω
35
36
3º-O circuito da figura esteve operando em estado permanente com a chave K
aberta para todo t < 0. Se não há nenhuma energia armazenada inicialmente na
capacitância e se a chave fecha em t = 0, determine e0(t) para todo t > 0.
K
2Ω
2Ω
1/2F
e0(t)
2H
4V
III.8- A Resposta Forçada a εSt .
Na resposta forçada à entrada x ( t ) St , onde “S” é um parâmetro
independente e constante em relação a “t”, a solução particular tem a forma
y P ( t ) H (S) . St , onde H (S) é um fator multiplicativo cujo valor depende do
parâmetro “s” mas não de “t”.
Se x ( t ) st → y P ( t ) H (S) . St , que diferenciando, temos:
an
dn y
dt n
a n 1
d n 1 y
dt n 1
dy
dmx
d m 1x
dx
... a1
a 0 y b m m b m 1 m 1 ... b1
b0 x
dt
dt
dt
dt
Ou seja;
a n H (s)Sn st a n 1H (s)Sn 1 st ... a1H (s)S st a 0 H (s) st
b mSm st b m 1Sm 1 st ... b1S st b 0 st
H (s) a n Sn a n 1Sn 1 ... a1S a 0 b mSm b m 1Sm 1 ... b1S b 0
Explicitando H (s ) , teremos:
H (s )
b mSm b m 1Sm 1 ... b1S b 0
a n Sn a n 1Sn 1 ... a1S a 0
Note que H (s ) é o quociente de dois polinômios em “S” onde os coeficientes do
numerador e denominador são iguais aos coeficientes do lado direito e do lado
esquerdo da equação diferencial.
H (s ) é chamada de “Função de circuito”.
36
37
Obs.:
1ª-H(s) pode ser escrita por inspeção da equação diferencial.
2ª-Se conhecermos H(s) a equação diferencial pode ser reconstituída.
Exemplo 1 => Determine no circuito abaixo a resposta forçada a i1 ( t ) t .
i1(t)
C
R
e0(t)
Exemplo 2 => Determine a resposta forçada do circuito do exemplo 1 para uma
entrada i1(t) = coswt.
IV- O Estado Permanente em Corrente Alternada.
Uma fonte que gera um sinal de forma senoidal com amplitude constante é
conhecida como Fonte de Corrente Alternada.
Este tipo de fonte é muito utilizada em sistemas de potência e em sistemas
eletrônicos, representando, portanto um caso muito importante. Sabemos também que
qualquer sinal periódico pode ser estudado como uma soma de sinais senoidais pela
série de Fourier, e logo que a resposta em estado permanente CA do circuito é
conhecida, a resposta a esse sinal periódico pode ser determinada utilizando
superposição. Neste estudo, admitiremos que a resposta livre YH(t) se anula quando t
→ ∞ de modo que a resposta forçada YP(t) será a resposta em estado permanente
YSS(t).
IV.1- Revisão de Números complexos.
Um número complexo Z é um número da forma z = x +jy, onde x e y são reais
ej=
1 . Neste número complexo o primeiro termo x é chamado de parte real e o
termo y de parte imaginária. Essas partes real e imaginária são representadas em
eixos cartesianos, onde a parte real ocupa o eixo das abcissas e a imaginária o eixo
das ordenadas. Os dois eixos formam um plano chamado de Plano Complexo.
37
X e Z
38
Y I m Z
e
Represente os números complexos dados no plano complexo:
z1 4 j2 ; z 2 2 ; z 3 j3 ; z 4 2 j2
IV.1.1- Formas de se representar um número complexo.
Im
z x jy Forma re tan gular
z
y
z r (cos jsen ) Forma trigonomét rica
z r j Forma exp onencial
z r Forma polar
r
θ
0
x
Re
onde r x 2 y 2
; arctg
y
x
IV.1.2- Conjugado de um número complexo.
É um outro número complexo que multiplicado pelo primeiro resulta em um
número real puro.
Se,
z x jy z* x jy
z r (cos jsen ) z* r (cos jsen )
z r j z* r j
z r z* r
IV.1.3- Soma e diferença de números complexos.
A soma ou a diferença de números complexos são feitas na forma retangular.
Seja, z1 = x1 + jy1 e z2 = x2 + jy2
z1 + z2 = (x1 + x2) +j(y1 + y2) ; z1 – z2 = (x1 – x2) +j(y1 – y2)
IV.1.4- Multiplicação de números complexos.
Pode tanto ser efetuada na forma polar quanto nas outras, mas na prática, é
recomendável na forma polar ou exponencial.
38
39
z1 r1
j1
r11 e z 2 r2
j 2
r2 2
z1.z 2 r1.r2 j(1 2 ) r1.r21 2
IV.1.5- Divisão de números complexos.
A forma mais prática é na polar ou exponencial.
z1 r1 j1
r1 j(1 2 )
z 2 r2 j 2 r2
;
z1 r11 r1
1 2
z 2 r2 2 r2
IV.1.6- Raiz de número complexo.
Se z1 r1
j1
n z1 n r1 .
Ou se z1 r11
n
n
j1
n r1
z1 n r1
j 1
. n
1
n
IV.2- Representação de Funções Senoidais do Tempo.
IV.2.1- Introdução.
Seja a função f(t) = Fmcos(wt + Φ)
f(t)
Fm
t
Fm → Amplitude, valor máximo.
W → Freqüência angular, pulsação (rad/s)
Depende da fonte.
Φ → Ângulo de fase da função em relação
a uma onda cossenoidal pura.
f → Freqüência da fonte (Hz) ; W = 2πf
Φ
IV.2.2- Fasores Girantes.
j cos jsen
Fórmulas de Euler j
cos jsen
j j
cos
2
Corolários
j
j
sen
j2
39
40
Seja a função f ( t ) Fm cos( wt ), que pode ser reescrita como:
Fm cos(wt )
1
1
Fm j( wt ) Fm j( jwt ) Fm j jwt Fm j jwt =
2
2
1 jwt
jwt
j
F F
, onde F Fm é uma constante complexa e F é o seu
2
complemento conjugado.
Para um dado valor de “t”, as duas funções complexas F
jwt
e F jwt podem ser
representadas num plano complexo por segmentos orientados, conforme figura:
Im
À medida que “t” aumenta, os dois segmentos orientados
giram em sentidos opostos, gerando o lugar geométrico de uma
circunferência, sendo por esta razão denominados “Fasores
Girantes em sentidos contrários”.
Para todos os valores do tempo, metade da soma dos
fasores girantes em sentidos contrários resulta na função real
F jwt
Fm
0
Wt + Φ
- (Wt + Φ)
Fm
1 jwt
f ( t ) F F jwt .
2
Real
Note que f(t) é também igual à projeção de qualquer
jwt
deles no eixo real, ou seja, f ( t ) ReF .
F jwt
Portanto, não há necessidade de mostrar explicitamente ambos os fasores
girantes para se reconstruir f(t). Por convenção, mantém-se o fasor que gira no
sentido anti-horário.
Se X jwt é o fasor girante anti-horário de entrada, a resposta forçada a este tem a
forma Y jwt , que é outro fasor girante com a mesma freqüência angular de rotação,
conforme figura:
Im
X jwt X m j( wt 1 )
α
0
Y
β
jwt
Ym
j( wt 2 )
α=Wt + Φ1
β=Wt + Φ2
Real
40
41
Podemos observar que a projeção dos fasores girantes X X m j1 e Y Ym j 2 no
eixo real dá as funções senoidais x(t) = Xmcos(wt + Φ1) e y(t) = Ymcos(wt + Φ2)
respectivamente.
Portanto o termo fasor é entendido como sendo o valor do fasor girante em sentido
anti-horário no instante t = 0.
1 jwt
Se f ( t ) Fm cos(wt ) F F jwt , o fasor F Fm j Fm .
2
IV.2.3- Resposta de um circuito à função f(t) = Fmcos(wt + Φ).
Se f(t) é a entrada e é a parte real de Fmεj(wt + Φ) , a saída a f(t) será a parte real da
saída à entrada complexa Fmεj(wt + Φ) .
Sabemos que a saída relativa à entrada X(t) = KεSt será Y(t) = H(S) KεSt .
Se
X(t ) X m
j( wt )
j jwt
X m
onde X m
j
X m X Fasor de entrada.
Logo, Y( t ) H ( jw ) jwt
Relacionando por derivadas a saída Y(t) e a entrada X(t), tem-se H(jw) sendo um
número complexo, dado pela relação:
H ( jw )
b m ( jw ) m b m 1 ( jw ) m 1 ..... b1 ( jw ) b 0
a n ( jw ) n a n 1 ( jw ) n 1 ..... a1 ( jw ) a 0
Y H ( jw ) . X
Conclusão: Se tivermos o fasor X , o circuito (an ; bm) e a freqüência, podemos obter
o fasor Y . Multiplicando-se este fasor Y por jwt e tomando a parte real, obtemos a
resposta à função f ( t ) Fm cos( wt ) .
41
42
Exemplo1: Determine a saída e0(t), no circuito.
1K
e1(t) =100cos(100t + 30°) volts
1μF
e1(t)
e0 (t)
Exemplo2: Determine a tensão de saída em estada permanente e0(t) no circuito da
figura, onde e1(t) = 20cost volts.
L=2H
e1(t)
R1=4Ω
C=1F
R2=1/2Ω
e0 (t)
IV.3- Impedância e Admitância
Considere a rede passiva abaixo:
jwt
e( t ) E máx cos(wt 1 ) e E .
i( t ) I m´x cos(wt 2 ) e I . jwt
→ i(t)
REDE
e(t)
PASIVA
e E . jwt
e( t )
i( t )
e I . jwt
E
Z
I
Z
E
, onde Z é a impedância complexa do circuito;
I
Y
I
siemens , onde Y é a admitância complexa do circuito.
E
IV.3.1- Resistência
e( t ) R.i( t ) E . jwt R. I . jwt onde R
E
Z
I
42
43
IV.3.2- Capacitância
de( t )
jwt
i( t ) C
I . C. E jw . jwt
dt
ZC
I jwC E
E
I
1
jwC
1
1
1
ou Z C j
ou Z C
90
jwC
wC
wC
IV.3.3- Indutância
di( t )
e( t ) L
E . jwt L. I jw . jwt
dt
E jwL I
E
jwL
I
Z L jwL ou Z L wL90
Exemplo: Determine a tensão de saída e0(t) para o circuito a seguir, quando
e1(t)=10cos(10t + 20°) volts. Dados R0=R1=1/2Ω; R2=1Ω; L1=1/10H; L2=1/5H;
L1
C=1/10F.
R1
L2
C
e1(t)
R0
e0 (t)
R2
IV.4- Diagramas Fasoriais
e1 ( t ) E1 cos(wt 1 )
Suponha que num mesmo circuito
e 2 ( t ) E 2 cos(wt 2 )
jwt
e
(
t
)
e
E1
1
, logo e ( t ) e ( t ) e E E jwt .
Ou
1
2
2
1
e ( t ) e E jwt
2
2
A adição de duas funções senoidais do tempo de mesma freqüência pode ser
efetuada somando os seus fasores. Como os fasores são representados por segmentos
orientados, fasores tensão em elementos em série; fasores corrente de elementos em
paralelo podem ser somados graficamente (vetorialmente).
43
44
A finalidade de um diagrama fasorial é de mostrar os módulos e os ângulos
de defasagem entre eles. Qualquer um pode ser escolhido como referência
arbitrariamente. O diagrama fasorial assim conhecido poderá ser ajustado
posteriormente para dar a resposta a uma entrada de módulo e ângulo especificados.
Notas:
1ª-Para resistências, os fasores E e I estão em fase.
2ª-Para capacitâncias, o fasor I está adiantado de 90° do fasor E .
3ª-Para indutâncias, o fasor I está atrasado de 90° do fasor E .
4ª-Para circuitos RC o fasor I se adianta do fasor E de um ângulo entre 0° e 90°.
5ª-Para circuitos RL o fasor I se atrasa do fasor E de um ângulo entre 0° e 90°.
6ª-Para circuitos RLC os fasores I ou E podem estar adiantados ou atrasados um em
relação ao outro.
Exemplo1: Faça o diagrama fasorial de um circuito RLC série, supondo ZC > ZL.
Exemplo2: Faça o diagrama fasorial de um circuito RLC paralelo, supondo ZC > ZL .
Exemplo3: Traçar o diagrama fasorial do circuito abaixo;
L
e (t)
R1
C
R2
Aplicações.
1-Determine a equação diferencial relacionando e1(t) e e0(t) na figura. Calcule a
resposta em estado permanente a e1(t) = 2cos2t volts pelos métodos:
a) A solução clássica da equação diferencial;
b) O uso da função de circuito em estado permanente CA.
44
2Ω
45
1/3F
e1(t)
6Ω
e0 (t)
3Ω
2-Determine H(jw) para o circuito da figura abaixo, pelos métodos:
a)Encontre primeiro a equação diferencial que relaciona e1(t) e i0(t);
b)Caracterize os elementos passivos por suas impedâncias.
1/4F
i0(t)
1H
2Ω
e1(t)
2Ω
IV.5- Circuitos contendo fontes de diferentes frequências.
Um circuito no domínio do tempo que contenha fontes independentes de
freqüências diferentes não pode ser desenhado por um único circuito no domínio da
freqüência, pois as impedâncias das indutâncias e capacitâncias são diferentes. Ainda
mais, não existe meio de se combinar fasores de funções senoidais com diferentes
freqüências.
Sejam as funções abaixo expressas como as projeções no eixo real de seus
fasores girantes em sentido anti-horário;
f1 ( t ) e F1 jw 1 t e Fm1 j1 jw 1 t
f 2 ( t ) e F2 jw 2 t e Fm 2 j 2 jw 2 t
a) Se w2 = w1, temos:
f1 ( t ) f 2 ( t ) e F1 jw 1 t F2 jw 1 t e F1 F2 jw 1 t
onde F1 F2 FR Fasor resul tan te
45
46
b) Se w2 ≠ w1, temos que;
f1 ( t ) f 2 ( t ) eF1 jw 1t F2 jw 2 t , F1 e F2 não podem ser combinados.
Observação: Quando um circuito contem fontes independentes de freqüências
diferentes, a resposta em estado permanente a cada fonte independente deverá ser
determinada como uma função do tempo separada e a resposta completa poderá ser
finalmente escrita por superposição.
Exemplo1: Determine a tensão de saída em estado permanente eo(t) no circuito da
figura, onde a entrada e1 ( t ) 3 10 cos t 3 cos( 3t 30) volts .
L1=1 H
e1(t)
R1=4 Ω
R2=1/2Ω
e0 (t)
C=1F
Exemplo2: Determine eo(t) no estado permanente para o circuito da figura;
1/4F
1/2 H
e1(t) =2 + 2cos2t
2Ω
e0(t)
e2(t)=3sen2t
IV.6- Combinação de termos trigonométricos por soma de fasores.
Se tivermos termos trigonométricos com a mesma freqüência angular, a soma
desses termos poderá ser expressa como um único termo trigonométrico com um
ângulo de fase.
Pelo uso de identidades apropriadas, pode ser mostrado que:
2
2
1 B
A B cos wt tg A
A cos wt Bsenwt
A 2 B2 sen wt tg 1 A
B
46
47
Cada um dos termos trigonométricos a ser combinado pode ser representado
por um fasor. Se A e B são ambas constantes positivas, os fasores que representam
Acoswt e Bsenwt = Bcos(wt – 90°) são mostrados a seguir:
- sen
1 tg 1
A
- cos
B
ө2
B
A
A
2 tg 1
B
cos
ө1
A 2 B2
sen
Exemplo. Represente por um único termo em cos e sen as somas:
a) – 5senwt + 12coswt
b) 4senwt – 2coswt
Aplicações.
1-Se L = 1mH, C = 1nF, R = 2KΩ e i1(t) = cos106t na figura abaixo, determine a
resposta em estado permanente.
R
i1(t)
e0 (t)
C
L
2-Determine e0(t) no
estado permanente para o circuito dado, quando
e1(t)=20cos(5t+45°) volts.
1Ω
e1(t)
1/2F
2H
1/2F
2H
10Ω
e0(t)
47
48
V- Freqüência Complexa.
V.1- Representação de oscilações crescentes e decrescentes.
1 jwt
Foi visto que a função f1 ( t ) F F jwt é uma função senoidal de
2
amplitude constante que pode ser escrita:
f1 (t ) Fm cos(wt )
1
Fm j jwt Fm j jwt .
2
Considere a função a seguir f 2 ( t ) , como:
f 2 ( t ) Fm t cos(wt )
1
Fm t j jwt Fm t j jwt
2
1
Fm j ( jw ) t Fm j ( jw ) t
2
A função f 2 ( t ) se reduz a f1 ( t ) quando o parâmetro σ (que pode assumir qualquer
valor real) for zero.
A seguir vamos esboçar graficamente a função f 2 ( t ) para vários valores diferentes de
σ e w:
a) Para σ < 0
f2(t)
Fmε
σt
t
Oscilação decrescente
b) Para σ > 0
f2(t)
Fmε
σt
t
Oscilação crescente
48
49
c) Para σ = 0
f2(t)
t
Oscilação constante
d) Para σ < 0 e w = 0
f2(t)
t
Exponencial decrescente
e) Para σ > 0 e w = 0
f2(t)
t
Exponencial crescente
t
Constante
e) Para σ = 0 e w = 0
f2(t)
Assim
como
a
função
f1 ( t ) Fm cos( wt ) ,
a
função
f 2 ( t ) Fm t cos( wt ) pode ser expressa como a metade da soma dos fasores
girantes em sentidos contrários (Fm j ) ( jw ) t e (Fm j ) ( jw ) t , ou como a
projeção no eixo real do vetor que gira em sentido anti-horário, conforme figura;
49
50
Im
(Fm j ) ( jw ) t
Fmεσt
0
Wt + Φ
- (Wt + Φ)
Fmεσt
Real
(Fm j ) ( jw ) t
Os fasores girantes movem-se novamente com uma velocidade angular w, mas
a menos que σ = 0, o seu comprimento também se alterará com o tempo.
Se σ < 0, os fasores girantes traçam uma espiral decrescente, conforme figura;
Se σ > 0, os fasores girantes traçam uma espiral crescente, conforme figura;
50
51
Obs.: Para o caso especial de w = 0, eles não giram, mas somente diminuem ou
aumentam de tamanhos.
No fasor girante em sentido anti-horário (Fm j ) ( jw ) t , temos:
W → velocidade angular (taxa de variação do ângulo) em rad/s;
σ → taxa logarítmica de redução ou de crescimento em tamanho, em neper/s.
1 neper = 0,434 bel
Podemos observar que os valores de w e σ determinam a natureza do fasor
girante em sentido anti-horário e a natureza da função f 2 ( t ) . Portanto defini-se a
freqüência complexa como, S jw , onde S é uma grandeza complexa sendo uma
generalização da resposta em estado permanente de corrente alternada estudada
anteriormente.
A grandeza complexa F Fm j Fm é o valor do fasor girante em sentido
anti-horário em t = 0.
Portanto, Fm j ( jw ) t F st .
Se x ( t ) X st é uma entrada e y( t ) Y st for a resposta forçada, então,
Y H (s ) . X . Se as grandezas dessa equação forem expressas na forma polar, ou seja:
X X m j ; H(s) H(s) j ; Y Ym j , logo, o módulo e o ângulo do fasor
de saída Y , são dados por:
Ym H (s) .X m ;
Para o cálculo de H (s ) , usa-se o valor de S jw , que corresponde ao sinal de
entrada x ( t ).
Se x ( t ) X m t cos(wt 1 ) X st , a resposta forçada será:
st
y p ( t ) Ym cos(wt 2 ) Y .
t
51
52
Exemplo1: Determine a resposta forçada do circuito da figura à entrada
i1 ( t ) 2 t cos t A .
σ = 1 neper/s; w = 1 rad/s; s = (-1 + j)
i1(t)
2F
1/6Ω
e0 (t)
I1 20 A
V.2- Impedância e Admitância.
A função de circuito H(S) que aparece na equação Y H (s ) X , não é
normalmente determinada a partir da equação diferencial do circuito.
Seja o fasor girante em sentido anti-horário x ( t ) X st dado como entrada.
Na obtenção da resposta forçada, a tensão e a corrente de um elemento típico de dois
terminais devem ter uma forma semelhante, ou seja:
e( t ) E(s) st ,
i(t ) I(s) st
Os fasores E e I não são funções do tempo e seus valores dependem do valor de s,
que por sua vez, é determinado pela fonte.
a) Elemento típico Resistência.
A equação e( t ) Ri(t ) se torna E(s) st R I(s) st , de forma que
E(s)
R.
I(s)
b) Elemento típico Capacitância.
E(s) 1
de( t )
A equação i( t ) C
se torna I(s) st sC E(s) st , de forma que
.
sC
dt
I(s)
c) Elemento típico Indutância.
E(s)
di(t )
st
A equação e( t ) L
se torna E(s) sL I(s) st , de forma que sL .
dt
I(s)
52
53
d) A impedância Z(s)
E(s)
1
e) A admitância Y(s)
Z(s)
I(s)
I(s)
E(s)
Quadro resumo da impedância e admitância dos três elementos passivos.
Resistência
Z(s) = R
Y(s)=1/R
Estado permanente de Estado permanente de
corrente alternada
corrente contínua
Z(jw) = R
Z(0) = R
Capacitância
Z(s) = 1/sC
Y(s) = sC
Z(jw) = 1/jwC
Indutância
Z(s) = sL
Y(s) = 1/sL
Z(jw) = jwL
Elemento
Expressões gerais
Z(0) →∞
(Circuito aberto)
Z(0) = 0
(Curto-circuito)
A função de circuito H(s) será obtida da relação entre os fasores de saída e entrada,
ou seja:
H (s)
Y
X
Exemplo2: Determine a função H(s) para o circuito da figura.
1/10H
1/2Ω
1/5H
1/10F
1/2Ω
e1(t)
e0(t)
1Ω
Exemplo3: Determine a resposta forçada para o exemplo2 a cada uma das entradas:
a) e1 ( t ) 5 3t cos( t 10) volts
b) e1 ( t ) 10 cos(10 t 20) volts
c) e1 ( t ) 10 t volts
d) e1 ( t ) 10 volts
53