Preparação Prova final 9 ano – Ficha 1

Prova Modelo – Ficha 1
Exercício 1
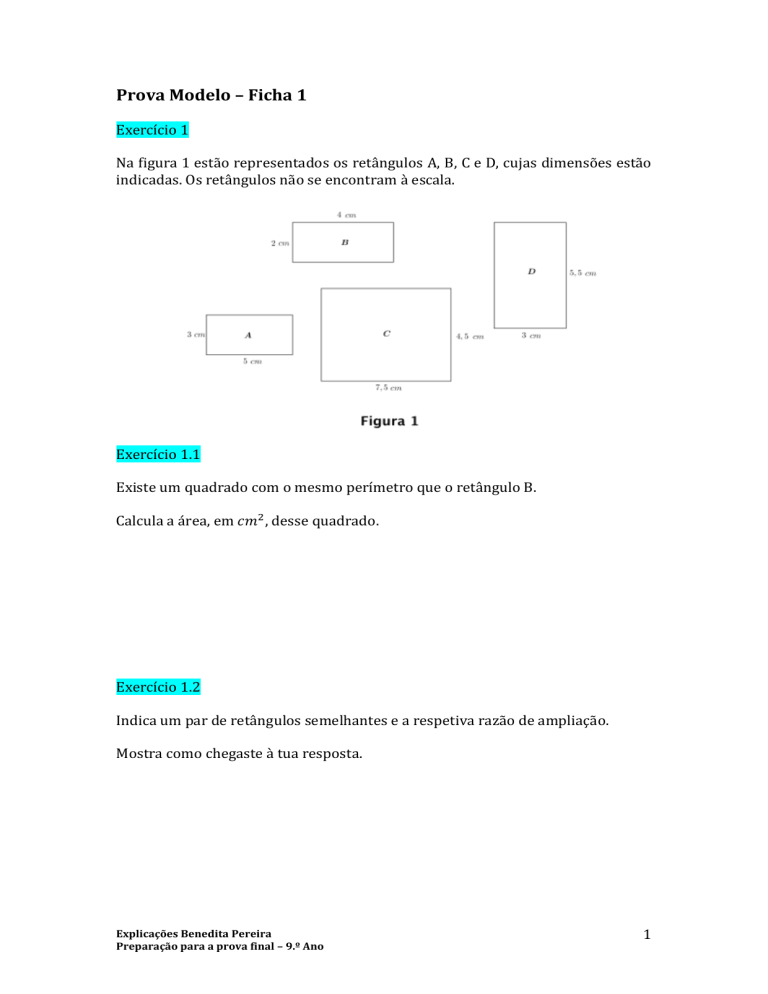
Na figura 1 estão representados os retângulos A, B, C e D, cujas dimensões estão
indicadas. Os retângulos não se encontram à escala.
Exercício 1.1
Existe um quadrado com o mesmo perímetro que o retângulo B.
Calcula a área, em 𝑐𝑚2 , desse quadrado.
Exercício 1.2
Indica um par de retângulos semelhantes e a respetiva razão de ampliação.
Mostra como chegaste à tua resposta.
Explicações Benedita Pereira
Preparação para a prova final – 9.º Ano
1
Exercício 1.3
O Luís desenhou um novo retângulo. A razão de semelhança entre o novo
retângulo e o retângulo D é 2.
Qual a área, em 𝑐𝑚2 , do novo retângulo?
Assinala a opção correta.
8,5
16,5
33
66
Exercício 1.4
Considere o retângulo B inscrito numa circunferência.
Calcula o valor exato, em 𝑐𝑚, do raio dessa circunferência.
Mostra como chegaste à tua resposta.
Exercício 2
O Luís tem no bolso três moedas de 1€ e 2 moedas de 0,50€. Para pagar a
despesa retira do bolso duas moedas, uma após a outra.
Exercício 2.1
De quantas formas diferentes pode o Luís tirar 1,50€?
Mostra como chegaste à tua resposta.
Explicações Benedita Pereira
Preparação para a prova final – 9.º Ano
2
Exercício 2.2
Calcula a probabilidade do Luís retirar duas moedas de 1€?
Apresenta a resposta na forma de fração irredutível.
Mostra como chegaste à tua resposta.
Exercício 3
Qual é o menor dos seguintes números?
Assinala a opção correta.
2
1
9
1
√9
1 2
( )
9
1
9
2
Exercício 4
Resolve a equação seguinte.
3𝑥 2 + 3𝑥 = 𝑥 + (𝑥 + 2)2
Apresenta os cálculos que efetuares.
Explicações Benedita Pereira
Preparação para a prova final – 9.º Ano
3
Exercício 5
Um circo recebeu 483 euros pela venda de bilhetes, no espetáculo dum dia.
Nesse dia, o número dos bilhetes vendidos para adultos foi um terço do número
dos bilhetes vendidos para crianças. Os bilhetes de adulto custavam 8 euros e os
bilhetes de criança 5 euros.
Determina quantos bilhetes de criança e quantos bilhetes de adulto foram
vendidos nesse dia.
Mostra como chegaste à tua resposta.
Exercício 6
Considera os conjuntos 𝐴 = ]−3, 2] e 𝐵 = ]−∞, −1[.
Qual dos seguintes conjuntos é igual a 𝐴 ∪ 𝐵 ?
]−∞, −1]
]−1, 2[
]−1, 2]
]−∞, 2]
Exercício 7
Resolve a seguinte inequação.
𝑥
− 4 ≤ 2(−5 + 𝑥)
3
Apresenta o conjunto solução na forma de intervalo de números reais.
Apresenta os cálculos que efetuares.
Explicações Benedita Pereira
Preparação para a prova final – 9.º Ano
4
Exercício 8
Seja 𝑛 um número natural, diferente de 1.
Sabendo que 𝑛4 = 𝑘.
Qual é o valor de 𝑛8 ?
Assinala a opção correta.
𝑘4
𝑘2
√𝑘
2𝑘
Exercício 9
Indica o termo geral da sequência seguinte.
3
7
11
15
…
Exercício 10
O Luís aproveitou uma tarde de trovoada para fazer um trabalho para
matemática. Em casa foi registando o tempo em segundos entre o relâmpago e o
trovão e a distância, em quilómetros, em que ocorre o relâmpago.
Após a recolha do tempo e correspondente distância, construi a Tabela 1.
Tempo
(segundos)
Distância
(quilómetros)
5
10
15
20
30
1,7
3,4
5,1
6,8
10,2
Tabela 1
Explicações Benedita Pereira
Preparação para a prova final – 9.º Ano
5
Exercício 10.1
A correspondência representada pela Tabela 1 é uma função. Indica a variável
independente e a variável dependente.
Exercício 10.2
Constrói um gráfico representativo da relação entre o tempo (segundos) e a
distância (quilómetros).
Exercício 10.3
Qual é a imagem de 15?
Assinala a opção correta.
5
1,7
Explicações Benedita Pereira
Preparação para a prova final – 9.º Ano
5,1
10
6
Exercício 10.4
A que distância ocorre a trovoada se o tempo entre o relâmpago e o trovão for de
1,25 minutos?
Mostra como chegaste à tua resposta.
Exercício 11
Figura 2
Observa o polígono regular da Figura 2. A figura não está desenhada à escala.
Sabendo que o comprimento do segmento ED é igual a 20 metros, calcula a área
do polígono ABCDEF.
Apresenta o resultado em 𝑚2 , com duas casas decimais. Sempre que, em cálculos
intermédios, procederes a arredondamentos, conserva, no mínimo, três casas
decimais.
Bom trabalho 
Explicações Benedita Pereira
Preparação para a prova final – 9.º Ano
7
Cotação
𝟏. 𝟏
6
𝟑
5
𝟗
5
𝟏. 𝟐
6
𝟒
6
𝟏𝟎. 𝟏
6
𝟏. 𝟑
5
𝟓
6
𝟏𝟎. 𝟐
6
Explicações Benedita Pereira
Preparação para a prova final – 9.º Ano
𝟏. 𝟒
6
𝟔
5
𝟏𝟎. 𝟑
5
𝟐. 𝟏
5
𝟕
6
𝟏𝟎. 𝟒
5
𝟐. 𝟐
6
𝟖
5
𝟏𝟏
6
8
Formulário
Números
Valor aproximado de 𝜋 (pi): 3,14159
Geometria
Perímetro de um círculo: 2𝜋𝑟, sendo 𝑟 o raio do círculo
Áreas
Paralelogramo: 𝑏𝑎𝑠𝑒 × 𝑎𝑙𝑡𝑢𝑟𝑎
Losango:
𝑑𝑖𝑎𝑔𝑜𝑛𝑎𝑙 𝑚𝑎𝑖𝑜𝑟 × 𝑑𝑖𝑎𝑔𝑜𝑛𝑎𝑙 𝑚𝑒𝑛𝑜𝑟
Trapézio:
2
𝑏𝑎𝑠𝑒 𝑚𝑎𝑖𝑜𝑟+𝑏𝑎𝑠𝑒 𝑚𝑒𝑛𝑜𝑟
2
Polígono regular: 𝑎𝑝ó𝑡𝑒𝑚𝑎 ×
× 𝑎𝑙𝑡𝑢𝑟𝑎
𝑝𝑒𝑟í𝑚𝑒𝑡𝑟𝑜
2
Círculo: 𝜋𝑟 2 , sendo 𝑟 o raio do círculo
Superfície Lateral do cone: 𝜋𝑟𝑔, sendo 𝑟 o raio da base do cone e 𝑔 a geratriz
Superfície da esfera: 4𝜋𝑟 2, sendo 𝑟 o raio da esfera
Volumes
Prisma e cilindro: á𝑟𝑒𝑎 𝑑𝑎 𝑏𝑎𝑠𝑒 × 𝑎𝑙𝑡𝑢𝑟𝑎
1
Pirâmide e cone: 3 × á𝑟𝑒𝑎 𝑑𝑎 𝑏𝑎𝑠𝑒 × 𝑎𝑙𝑡𝑢𝑟𝑎
4
Esfera: 3 𝜋𝑟 3
Álgebra
Fórmula resolvente de uma equação do segundo grau da forma 𝑎𝑥 2 + 𝑏𝑥 + 𝑐 :
𝑥=
−𝑏 ± √𝑏 2 − 4𝑎𝑐
2𝑎
Trigonometria
Fórmula fundamental: 𝑠𝑒𝑛2 𝑥 + 𝑐𝑜𝑠 2 𝑥 = 1
Relação da tangente com o seno e o cosseno: 𝑡𝑔 𝑥 =
Explicações Benedita Pereira
Preparação para a prova final – 9.º Ano
𝑠𝑒𝑛 𝑥
cos 𝑥
9
Tabela trigonométrica
Graus
Seno
Cosseno
Tangente
Graus
Seno
Cosseno
Tangente
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
0,0175
0,0349
0,0523
0,0698
0,0872
0,1045
0,1219
0,1392
0,1564
0,1736
0,1908
0,2079
0,2250
0,2419
0,2588
0,2756
0,2924
0,3090
0,3256
0,3420
0,3584
0,3746
0,3907
0,4067
0,4226
0,4384
0,4540
0,4695
0,4848
0,5000
0,5150
0,5299
0,5446
0,5592
0,5736
0,5878
0,6018
0,6157
0,6293
0,6428
0,6561
0,6691
0,6820
0,6947
0,7071
0,9998
0,9994
0,9986
0,9976
0,9962
0,9945
0,9925
0,9903
0,9877
0,9848
0,9816
0,9781
0,9744
0,9703
0,9659
0,9613
0,9563
0,9511
0,9455
0,9397
0,9336
0,9272
0,9205
0,9135
0,9063
0,8988
0,8910
0,8829
0,8746
0,8660
0,8572
0,8480
0,8387
0,8290
0,8192
0,8090
0,7986
0,7880
0,7771
0,7660
0,7547
0,7431
0,7314
0,7193
0,7071
0,0175
0,0349
0,0524
0,0699
0,0875
0,1051
0,1228
0,1405
0,1584
0,1763
0,1944
0,2126
0,2309
0,2493
0,2679
0,2867
0,3057
0,3249
0,3443
0,3640
0,3839
0,4040
0,4245
0,4452
0,4663
0,4877
0,5095
0,5317
0,5543
0,5774
0,6009
0,6249
0,6494
0,6745
0,7002
0,7265
0,7536
0,7813
0,8098
0,8391
0,8693
0,9004
0,9325
0,9657
1,0000
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
0,7193
0,7314
0,7431
0,7547
0,7660
0,7771
0,7880
0,7986
0,8090
0,8192
0,8290
0,8387
0,8480
0,8572
0,8660
0,8746
0,8829
0,8910
0,8988
0,9063
0,9135
0,9205
0,9272
0,9336
0,9397
0,9455
0,9511
0,9563
0,9613
0,9659
0,9703
0,9744
0,9781
0,9816
0,9848
0,9877
0,9903
0,9925
0,9945
0,9962
0,9976
0,9986
0,9994
0,9998
0,6947
0,6820
0,6691
0,6561
0,6428
0,6293
0,6157
0,6018
0,5878
0,5736
0,5592
0,5446
0,5299
0,5150
0,5000
0,4848
0,4695
0,4540
0,4384
0,4226
0,4067
0,3907
0,3746
0,3584
0,3420
0,3256
0,3090
0,2924
0,2756
0,2588
0,2419
0,2250
0,2079
0,1908
0,1736
0,1564
0,1392
0,1219
0,1045
0,0872
0,0698
0,0523
0,0349
0,0175
1,0355
1,0724
1,1106
1,1504
1,1918
1,2349
1,2799
1,3270
1,3764
1,4281
1,4826
1,5399
1,6003
1,6643
1,7321
1,8040
1,8807
1,9626
2,0503
2,1445
2,2460
2,3559
2,4751
2,6051
2,7475
2,9042
3,0777
3,2709
3,4874
3,7321
4,0108
4,3315
4,7046
5,1446
5,6713
6,3138
7,1154
8,1443
9,5144
11,4301
14,3007
19,0811
28,6363
57,2900
Explicações Benedita Pereira
Preparação para a prova final – 9.º Ano
10
Proposta de resolução:
Exercício 1
Exercício 1.1
Resolução:
O perímetro é a soma de todos os lados.
𝑃𝐵 = 2 × 2 + 2 × 4 <=> 𝑃𝐵 = 4 + 8 <=> 𝑃𝐵 = 12 𝑐𝑚
Logo, a medida do lado do quadrado, com o mesmo perímetro do retângulo, é 3
𝑐𝑚, porque 4 × 3 = 12 𝑐𝑚.
Calculemos a área desse quadrado:
𝐴𝑞𝑢𝑎𝑑𝑟𝑎𝑑𝑜 = 32 = 9 𝑐𝑚2
R: A área do quadrado com o mesmo perímetro que o retângulo B é 9 𝑐𝑚2 .
Exercício 1.2
Resolução:
Os retângulos A e C são semelhantes, pois os lados correspondentes são
proporcionais.
7,5 4,5
=
= 1,5
5
3
A razão de semelhança da ampliação é 1,5.
Exercício 1.3
Resposta:
8,5
16,5
33
𝑋 66
Cálculos auxiliares:
𝑥
𝑦
=
= 2 <=>
3 5,5
𝑥
=2
3
𝑦
=2
{5,5
𝑥=6
<=> {
Explicações Benedita Pereira
Preparação para a prova final – 9.º Ano
𝑦 = 11
11
Assim:
𝐴 = 6 × 11 <=> 𝐴 = 66
R: A opção correta é, 66.
Exercício 1.4
Resolução:
Consideremos o triângulo [𝐴𝐵𝐶], retângulo em B.
Pelo teorema de Pitágoras, vem que:
̅̅̅̅ 2 = 𝐴𝐵
̅̅̅̅2 + 𝐶𝐵
̅̅̅̅ 2 <=> 𝐴𝐶
̅̅̅̅ 2 = 42 + 22 <=> 𝐴𝐶
̅̅̅̅ 2 = 16 + 4 <=>
𝐴𝐶
<=> ̅̅̅̅
𝐴𝐶 2 = 20 <=> ̅̅̅̅
𝐴𝐶 = √20 <=> ̅̅̅̅
𝐴𝐶 = 2√5 𝑐𝑚
𝑑 = ̅̅̅̅
𝐴𝐶 <=> 𝑑 = 2√5 𝑐𝑚
Assim:
𝑟=
2√5
<=> 𝑟 = √5 𝑐𝑚
2
R: O raio dessa circunferência mede √5 𝑐𝑚.
Exercício 2
Exercício 2.1
Resolução:
Explicações Benedita Pereira
Preparação para a prova final – 9.º Ano
12
Vamos construir uma tabela, para concluirmos de quantas formas diferentes
pode o Luís tirar 1,50 €.
1€
1€
1€
1€
0,50 €
0,50 €
1€
2€
2€
2€
1,50 €
1,50 €
2€
1,50 €
1,50 €
1€
2€
2€
1,50 €
1,50 €
0,50 €
1,50 €
1,50 €
1,50 €
0,50 €
1,50 €
1,50 €
1,50 €
1€
1€
Pela observação da tabela, concluímos que existem 12 formas diferentes, de o
Luís retirar 1,50 €.
Exercício 2.2
Resolução:
Observemos novamente a tabela:
1€
1€
1€
1€
0,50 €
0,50 €
𝑝=
1€
2€
2€
2€
1,50 €
1,50 €
2€
1,50 €
1,50 €
1€
2€
2€
1,50 €
1,50 €
0,50 €
1,50 €
1,50 €
1,50 €
0,50 €
1,50 €
1,50 €
1,50 €
1€
1€
6
3
<=> 𝑝 =
20
10
Exercício 3
Resposta:
2
1
9
1
√9
1 2
𝑋 ( )
9
1
9
2
Cálculos auxiliares:
2
= 18
1
9
Explicações Benedita Pereira
Preparação para a prova final – 9.º Ano
13
1
√9
=
1
= 0, (3)
3
1 2
1
( ) =
≈ 0,0123
9
81
1
9 = 1 ≈ 0,0(5)
2 18
Exercício 4
Resolução:
3𝑥 2 + 3𝑥 = 𝑥 + (𝑥 + 2)2 <=>
<=> 3𝑥 2 + 3𝑥 = 𝑥 + 𝑥 2 + 4𝑥 + 4 <=>
<=> 3𝑥 2 − 𝑥 2 + 3𝑥 − 𝑥 − 4𝑥 − 4 = 0 <=>
<=> 2𝑥 2 − 2𝑥 − 4 = 0 <=>
<=> 𝑥 =
2 ± √4 − 4 × 2 × (−4)
<=>
2 × 2
<=> 𝑥 =
2 ± √4 + 32
2 ± √36
<=> 𝑥 =
<=>
4
4
<=> 𝑥 =
2±6
2−6
2+6
<=> 𝑥 =
∨ 𝑥=
<=>
4
4
4
<=> 𝑥 = −
4
8
∨ 𝑥 = <=> 𝑥 = −1 ∨ 𝑥 = 2
4
4
𝐶. 𝑆. = {−1, 2}
Exercício 5
Resolução:
𝑥 – número de bilhetes vendidos por criança
8
𝑥 + 5𝑥 = 483 <=> 8𝑥 + 15𝑥 = 1449 <=>
3
Explicações Benedita Pereira
Preparação para a prova final – 9.º Ano
14
<=> 23𝑥 = 1449 <=> 𝑥 =
1449
<=> 63 bilhetes de criança
23
Calculemos agora o número de bilhetes de adultos:
63 ×
1
= 21 bilhetes de adulto
3
Exercício 6
Resolução:
𝐴 = ]−3, 2]
𝐵 = ]−∞, −1[
Assim:
𝐴 ∪ 𝐵 = ]−∞, 2]
Resposta:
]−∞, −1]
]−1, 2[
]−1, 2]
𝑋 ]−∞, 2]
Exercício 7
Resolução:
𝑥
𝑥
− 4 ≤ 2(−5 + 𝑥) <=> − 4 ≤ −10 + 2𝑥 <=>
3
3
<=> 𝑥 − 12 ≤ −30 + 6𝑥 <=> 𝑥 − 6𝑥 ≤ −30 + 12 <=>
<=> −5𝑥 ≤ −18 <=> 5𝑥 ≥ 18 <=> 𝑥 ≥
𝐶. 𝑆. = [
18
5
18
, +∞[
5
Explicações Benedita Pereira
Preparação para a prova final – 9.º Ano
15
Exercício 8
Resolução:
Sabemos pelo enunciado que 𝑛4 = 𝑘, com 𝑛 ∈ ℕ\{1}
Assim:
2
8
4
𝑛 = (𝑛
⏟) = 𝑘 2
=𝑘
Resposta:
𝑘4
𝑋 𝑘2
√𝑘
2𝑘
Exercício 9
3 ⟶
⏟ 7⟶
⏟ 11 ⟶
⏟ 15
+4
+4
…
+4
Assim:
𝑢𝑛 = 4𝑛 + 𝑘
Determinemos o valor de 𝑘:
𝑢1 = 4 × 1 + 𝑘 <=> 3 = 4 + 𝑘 <=> 𝑘 = −1
Logo, o termo geral da sucessão é:
𝑢𝑛 = 4𝑛 − 1
Exercício 10
Exercício 10.1
Resposta:
Variável independente  tempo (segundos)
Variável dependente  distância (quilómetros)
Explicações Benedita Pereira
Preparação para a prova final – 9.º Ano
16
Exercício 10.2
Resolução:
Exercício 10.3
Resposta:
5
1,7
𝑋 5,1
10
Exercício 10.4
Resolução:
Esta função é uma função de proporcionalidade direta, em que a constante de
proporcionalidade é 0,34.
Assim:
𝑑
= 0,34 <=> 𝑑 = 0,34𝑡
𝑡
1,25 minutos são 75 segundos.
Então:
𝑑 = 0,34 × 75 <=> 𝑑 = 25,5 𝑘𝑚
R: Se o tempo entre o relâmpago e o trovão for de 1,25 minutos a distância a que
ocorre a trovoada é 25,5 quilómetros.
Explicações Benedita Pereira
Preparação para a prova final – 9.º Ano
17
Exercício 11
Resolução:
O hexágono regular pode ser dividido em 6 triângulos equiláteros iguais, com 20
metros de lado.
Num triângulo equilátero, a altura, divide a base ao meio.
Usando, o teorema de Pitágoras, temos:
202 = 102 + 𝑎𝑙𝑡 2 <=> 400 = 100 + 𝑎𝑙𝑡 2 <=> 𝑎𝑙𝑡 2 = 300 <=>
<=> 𝑎𝑙𝑡 = √300 <=> 𝑎𝑙𝑡 = 10√3 𝑚
Calculemos, agora, a área do hexágono:
𝐴ℎ𝑒𝑥á𝑔𝑜𝑛𝑜 = 6 ×
20 × 10√3
<=> 𝐴ℎ𝑒𝑥á𝑔𝑜𝑛𝑜 ≈ 1039,23 𝑚2
2
R: A área do polígono é de aproximadamente 1039,23 𝑚2 (valor aproximado
com duas casas decimais)
Explicações Benedita Pereira
Preparação para a prova final – 9.º Ano
18