Mecânica dos Fluidos Aula 202 – Conservação do Momento Linear

Mecânica dos Fluidos
Aula 202 – Conservação do Momento Linear
Utilizando o Teorema de Transporte de Reynolds e fazendo B=P=mV e b=mV/m=V:
𝑑𝑃
𝑑
⃗ ∙ 𝑑𝐴
= ∫ 𝜌𝑉𝑑∀ + ∫ 𝑉𝜌𝑉
𝑑𝑡 𝑑𝑡 ∀
𝐴
(1)
(2)
(1) Variação de momento no VC
(2) Quantidade de momento que atua pelas fronteiras do sistema
Mas vale notar que, da segunda lei de Newton:
𝐹 = 𝑚𝑎 = 𝑚
𝑑𝑉 𝑑𝑃
=
𝑑𝑡
𝑑𝑡
E fazendo:
𝐹 = 𝐹𝑠 + 𝐹𝐵
Pode-se escrever
𝐹𝑠 + 𝐹𝐵 =
𝑑
⃗ ∙ 𝑑𝐴
∫ 𝜌𝑉𝑑∀ + ∫ 𝑉𝜌𝑉
𝑑𝑡 ∀
𝐴
Essa é a chamada conservação do momento linear, ou 2ª lei de Newton escrita para
um volume de controle não acelerado.
Considerações comuns:
- Não há forças de campo agindo em uma direção
𝐹𝐵 = 0
- Força de superfície é oriunda de pressão
𝐹𝑠 = − ∫ 𝑃𝑑𝐴
1
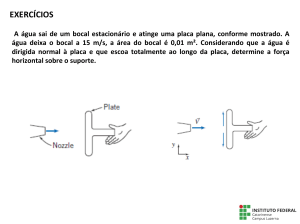
Exemplo 1: Água sai de um bocal estacionário e atinge uma placa plana como na
figura. A água deixa o bocal a 15m/s e a área do bocal é 0,01m 2. Considere que a água
atinge a placa normal à superfície e determine a força horizontal no suporte.
Considerações:
Regime permanente e velocidade constante pelas fronteiras do sistema
Equação:
⃗ ∙ 𝑑𝐴
𝐹𝑠 = ∫ 𝑉𝜌𝑉
𝐴
Solução
A pressão atmosférica age em todas as direções, então não há forças de pressão
atuando, apenas a resultante da força da água.
A força está “entrando” na superfície. Seu sinal deve ser negativo.
𝐹𝑠 = 𝑅𝑥 = ∫ 𝑉𝜌𝑉 ∙ 𝑑𝐴
𝐴
𝑅𝑥 = −𝑉𝜌𝑉𝐴
𝑅𝑥 = −15 ∙ 999 ∙ 15 ∙ 0,01 = −2,25𝑘𝑁
Exemplo 2: Um tanque de metal de 2ft de altura pesa 5lbf quando vazio e 1ft2 de área
de fundo. O container é colocado sobre uma balança enquanto água flui pela abertura
superior e vaza pelas aberturas laterais como mostrado na figura. Em condições de
regime permanente, o nível da água é de 1,9ft. A balança mede a massa do tanque
mais a da água ou há outras forças envolvidas?
2
Equação:
⃗ ∙ 𝑑𝐴
𝐹𝑠 + 𝐹𝑏 = ∫ 𝑉𝜌𝑉
𝐴
Solução
A pressão atmosférica age em todas as direções, então não há forças de pressão
atuando, apenas a resultante da força da água.
A força está “entrando” na superfície. Seu sinal deve ser negativo.
𝐹𝑠 + 𝐹𝑏 = ∫ 𝑉1 𝜌𝑉 ∙ 𝑑𝐴
𝐴
𝐹𝑠 + 𝐹𝑏 = −𝑉1 (−𝜌𝑉𝐴)
Note que V1 é para baixo e entrando. O Sinal fica positivo. Além disso:
𝐹𝑠 = 𝑅𝑦
E:
𝐹𝑏 = −(𝑊𝑡𝑎𝑛𝑞𝑢𝑒 + 𝑊𝑎𝑔𝑢𝑎 ) = −(𝑊𝑡𝑎𝑛𝑞𝑢𝑒 + 𝛾ℎ𝐴)
𝑅𝑦 − (𝑊𝑡𝑎𝑛𝑞𝑢𝑒 + 𝛾ℎ𝐴) = 𝑉1 𝜌𝑉𝐴
𝑅𝑦 = 𝑊𝑡𝑎𝑛𝑞𝑢𝑒 + 𝛾ℎ𝐴 + 𝑉1 𝜌𝑉𝐴
𝑅𝑦 = 5𝑙𝑏𝑓 + 62,4
𝑙𝑏𝑓
𝑠𝑙𝑢𝑔
𝑓𝑡 2
𝑠2
2
2
∙
1𝑓𝑡
∙
1,9𝑓𝑡
+
1,94
∙
100
∙
0,1𝑓𝑡
∙
𝑙𝑏𝑓
∙
𝑓𝑡 3
𝑓𝑡 3
𝑠2
𝑠𝑙𝑢𝑔 ∙ 𝑓𝑡
𝑅𝑦 = 5𝑙𝑏𝑓 + 118,6𝑙𝑏𝑓 + 19,4𝑙𝑏𝑓 = 143𝑙𝑏𝑓
3
Exemplo 3: Água flui em regime permanente pelo cotovelo da figura. Na entrada, a
pressão absoluta é 120kPa e a área da seção transversal é 0,01m2. Na saída, a área é
0,0025m2 e a velocidade é 16m/s. O cotovelo descarrega a água na atmosfera.
Determine a força necessária para o cotovelo ficar no local.
Equação:
𝑑
⃗ ∙ 𝑑𝐴
∫ 𝜌𝑉𝑑∀ + ∫ 𝑉𝜌𝑉
𝑑𝑡 ∀
𝐴
𝐹𝑠 + 𝐹𝐵 =
Solução:
Desprezando a derivada no tempo, a solução será dividida entre os eixos x e y.
Para o eixo x:
⃗ ∙ 𝑑𝐴
𝐹𝑠𝑥 = ∫ 𝑉𝜌𝑉
𝐴
⃗ ∙ 𝑑𝐴
𝑃1 𝐴1 + 𝑅𝑥 = ∫ 𝑉𝜌𝑉
𝐴
𝑅𝑥 = −𝑃1 𝐴1 − 𝜌𝑉12 𝐴1
𝑅𝑥 = −120𝑘 ∙ 0,01 − 1000 ∙ 𝑉12 ∙ 0,01
Qual o valor de V1?
Pela conservação da massa:
⃗ ∙ 𝑑𝐴 = 0
∫ 𝜌𝑉
𝐴
(𝜌𝑉𝐴)1 = (𝜌𝑉𝐴)2
𝑉1 = 𝑉2 ∙
𝐴2
0,0025
= 16 ∙
= 4𝑚/𝑠
𝐴1
0,01
4
Voltando na equação anterior:
𝑅𝑥 = −120𝑘 ∙ 0,01 − 1000 ∙ 42 ∙ 0,01
𝑅𝑥 = −1,35𝑘𝑁
Para o eixo y:
𝐹𝑠 + 𝐹𝐵 =
𝑑
⃗ ∙ 𝑑𝐴
∫ 𝜌𝑉𝑑∀ + ∫ 𝑉𝜌𝑉
𝑑𝑡 ∀
𝐴
Desprezando a massa do fluido, para efeitos de resultante:
⃗ ∙ 𝑑𝐴
𝑅𝑦 = ∫ 𝑉𝜌𝑉
𝐴
V2 é negativo (para baixo) e está saindo, logo o produto é negativo.
𝑅𝑦 = −𝑉2 𝜌𝑉2 𝐴2
𝑅𝑦 = 1000 ∙ 162 ∙ 0,0025
𝑅𝑦 = −640𝑁
5