exercícios segundo bimestre

EXERCÍCIOS PARA AVALIAÇÃO DO SEGUNDO BIMESTRE. TERMODINÂMICA
Instruções para resposta das perguntas:
-Leia as questões antes de respondê-las. A interpretação das questões faz parte da avaliação.
.
.
QVC  WVC
2
2
c
c
 m[( hs  he )  ( s  e )  g ( z s  ze )
2
2
.
.
.
.
0  QVC  WVC   me (he 
2
2
.
ce
c
 g e )   m s (hs  s  g s )
2
2
1)Nas usinas de potência a vapor, aquecedores de água de alimentação abertos (câmaras de
mistura) são utilizados com frequência misturando água com o vapor que é extraído da turbina
em estágios intermediários. Considere uma câmara de mistura que opere a uma pressão de 300
kPa. Água de alimentação entra com uma taxa de 1,8 kg/s. Se a mistura deixa a câmara a 60°C.
Determine a vazão mássica de vapor superaquecido assim como a vazão mássica de água na
saída da câmara de mistura.
Qm1
Qm3
Ponto 1: Água de alimentação
Ponto 2: Vapor superaquecido
Ponto 3: Água na saída do aquecedor
Qm2
Pontos
Qm1 = 1,8 kg/s
Qm2 = ?
Qm3 = ?
Temperatura (K)
293
573
333
h (kJ/kg)
80
3060
360
Dicas de solução:
Implicitamente o exercício considera que o trocador é adiabático, ou seja, sem interação térmica
com a vizinhança, e sendo que não produz trabalho, rapidamente é possível constatar que
chegamos a uma equação de balanço de massa:
Qm1 + Qm2 = Qm3
Sendo que, por exemplo:
Qm2 = Qm3 – 1,8
Por outro lado a equação de energia que aparece da análise da primeira lei indica:
Qm1h1 + Qm2h2 = Qm3
Se substituirmos Qm2 pela sua relação com Qm3 e Qm1, chegaremos à solução do exercício.
2) Quando um fluido escoa através de uma restrição, como um orifício, uma válvula parcialmente
fechada ou um tampão poroso, sem qualquer variação apreciável de energia cinética ou
potencial, e na ausência de transferência de calor, realiza-se um processo:
a) isotérmico.
b) isentálpico.
c) isentrópico.
d) isobárico.
e) isocórico.
Independentemente da sua escolha, fundamente sua resposta com relação ao item d
Dicas de solução
Analisando a primeira lei, é possível observar que, eliminando os termos das variações de
energia cinética e potencial, considerando o caráter adiabático do processo e a não realização ou
consumo de trabalho, chegamos à conclusão de que h1 = h2, portanto, trata-se de um processo
que pode ser considerado isentálpico, observando que numa válvula, sendo ela uma restrição ao
passo da corrente de um fluido, existe uma queda de pressão, sendo que não seria possível
considerar o processo como isobárico, ou seja, a pressão constante.
3) A vazão mássica de vapor d’água na seção de alimentação de uma turbina é 2 kg/s e o calor
transferido da turbina é 6,5 kW. São conhecidos os seguintes dados para o vapor d’água que
entra e sai da turbina:
Propriedade
Pressão
Temperatura
Entalpia específica
Condição de entrada
2,0 MPa
350 oC
3000 kJ
Condição de saída
0,1
2500 kJ
Variação da Energia Cinética por Massa 3,2 kJ/kg
Variação da Energia Potencial por Massa 0,05 kJ/kg
Determine a potência fornecida pela turbina.
4) O escoamento de massa transporta energia nas formas interna, potencial e cinética. Porem
devido a dificuldades de medidas exatas de energia interna a saída e considerar a energia
proveniente do escoamento para obtermos a entalpia como mostrado nas equações abaixo:
2
c
Ei  Qmi (hi  i  gzi ) Definida como a energia total que carrega um fluido em escoamento no
2
.
.
ponto i.
.
hi  ui  pi vi Correspondente à definição de entalpia de um ponto de um fluido em escoamento,
onde o termo pivi é denominado energia do escoamento.
Portanto o uso da entalpia no lugar na energia interna já considera o efeito da energia de
escoamento. Com base nisso verifique a seguinte situação. Um reator nuclear gera energia
térmica suficiente para aquecer a agua presente numa caldeira a 300•oC e pressão de 9 MPa.
Aproximadamente 3 kg de agua são transformados em vapor a cada 5 minutos e deixa o reator
na forma de vapor saturado passando por um a válvula de segurança de 10 mm 2 de área de
seção transversal.
Dados para a condição de vapor saturado a 9MPa:
Volume específico = 0,02 m3/kg
Entalpia especifica = 2700 kJ/kg
Energia interna especifica = 2550 kJ/kg
a) Calcule a velocidade de escoamento do vapor pela válvula de segurança.
b) Calcule a energia de escoamento e energia total.
Dicas de solução:
Interessante observar que de uma forma explicita, embora aparentemente não muito clara, a
vazão em massa é um dado do problema. Se 3 kg de água são transformados em vapor a cada
5 minutos, então 3 kg de vapor a cada 300 segundos são produzidos no reator.
Por outro lado, o volume específico é um inverso da densidade. Assim sendo é possível aplicar a
equação de continuidade a través da área da seção transversal da válvula (Olho com as
unidades!!!). Observe que nesse ponto já você tem vazão, densidade e área de seção
transversal. A única incógnita seria a velocidade.
Posteriormente, energia de escoamento = pv
Energia total, aplicar a primeira equação que aparece no texto do problema
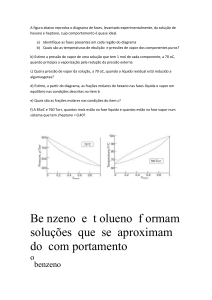
5-A potência gerada por uma turbina de vapor adiabática é de 5 MW e as condições de entrada e
saída do vapor são as indicadas, de acordo com a informação que aparece no diagrama
apresentado a seguir:
P1 = 2 MPa; T1 = 400 oC;
c1 = 50 m/s; z1 = 10m; h1 =
3248,4 kJ/kg
Wt = 5MW
P2 = 15 kPa; x2 = 90%;
c2 = 180 m/s; z2 = 6m
De acordo com a informação que aparece no diagrama, responda:
a)Explique baseado em cálculos por que a variação de energia potencial e cinética são muitas
vezes desprezíveis nos cálculos de potência a partir de primeira lei para volumes de controle
b)Determine o trabalho realizado pela unidade de massa do vapor que escoa na turbina
c)Calcule o fluxo de massa de vapor
Ts (oC)
uf (kJ/kg)
ug (kJ/kg)
hf (kJ/kg)
hg (kJ/kg)
10
45,81
191,79
2437,2
191,81
2583,9
15
53,97
225,93
2448,0
225,24
2598,3
20
60,06
251,40
2456,0
251,42
2608,9
25
64,96
271,93
2462,4
271,96
2617,5
P (kPa)
Dados de Tabela de saturação com entrada em pressão. Os subíndices f indicam líquido saturado, os subíndices g indicam vapor
saturado:
Dicas de solução:
Similar ao exercício 3. Só que no caso, o aluno deve conferir mediante cálculos, a pouca variação
de energia potencial e cinética aplicando a equação de balanço,... e assim é resolvido o item a)
Se a turbina é adiabática, uma equação de balanço de energia (pela unidade de massa), com
todos os dados, pode resolver essa situação (lembrando que Q = 0)
Pata determinar os parâmetros do ponto 2, o aluno deve usar o título do vapor x2 = 90%, usando
os dados do vapor e do líquido saturado para a pressão de saída do vapor da turbina, conforme
indicada nos dados.
O fluxo de massa de vapor é determinado pela relação W = wQm, onde w (trabalho específico
determinado no item b).
6-Para um volume de controle em regime permanente a situação da massa em seu interior e em
suas fronteiras não se altera com o tempo. As vazões mássicas e as taxas de transferências de
energia por calor e por trabalho não se alteram com o tempo. Muitas aplicações importantes
envolvem volumes de controle em regime permanente. Um desses casos é o caso do
compressor, que é um dispositivo no qual o trabalho é realizado sobre um gás que o atravessa
de modo a elevar a pressão.
Considere que ar a 1,05 Bar e 300 K entra em um compressor operando em regime permanente,
com uma vazão volumétrica de 12 m3/min. e sai a 12 bar e 400 K. A transferência de calor entre o
compressor e sua vizinhança ocorre a uma taxa de 2 kW. Admitindo o modelo de gás ideal para o
ar e desprezando os efeitos da energia potencial e cinética, determine a potência consumida pelo
compressor.
Considere o ar como um gás ideal, cujo valor de calor específico a pressão constante, aplicável
para os cálculos é 1,006 kJ/kg-K, e que a densidade do ar na entrada do compressor pode ser
considerado aproximadamente 1,2 kg/m3. Considere também o emprego da seguinte equação:
Δh = CpΔT
Dicas de solução:
Tome como referencia para solucionar o problema, que, conforme se indica o compressor não é
adiabático (Q = 2 kW). Desprezando as variações de energia cinética e potencial, e considerando
que o ar é um gás ideal, pode ser usado como uma boa aproximação o valor do calor específico
médio para a determinação da diferença de entalpia.
Não esqueça que previamente você deve determinar a vazão mássica (a vazão em volume é um
dado do problema), e para isso, você conta com a densidade do ar na condição de entrada no
compressor (Olho com as unidades!!!). Observar que a vazão volumétrica deve ser transformada
de m3/min a m3/s.
7-Os dispositivos de engenharia quase sempre operam em regime permanente, pois costumam
operar durante longos períodos antes de serem paralisados para manutenção. Portanto análise
em regime permanente para a equação da Primeira Lei da Termodinâmica aplicada a Volume de
Controle é frequentemente utilizada.
.
0  QVC
2
2
.
v
v
 WVC   Qm e (he  e  gz e )   Qm s (hs  s  gz s )
2
2
.
.
I – Válvulas de expansão são dispositivos que apresentam geração ou consumo de potência.
Além disso, as mesmas devem operar adiabaticamente, sendo desprezíveis as variações de
energia potencial e cinética.
II – Para um trocador de calor com 2 entradas e 1 saída de fluxo, sem acumulo de massa e com
as variações de energia cinética e potencial desprezíveis, a troca térmica com o ambiente pode
ser minimizada por meio de isolamento térmico, podendo assim ser considerada nula.
III – Um compressor não isolado termicamente possui uma entrada e uma saída de fluxo de ar,
tem como objetivo a realização de trabalho, sendo as variações de energia potencial e cinética
suficientemente pequenas para serem consideradas.
IV - Uma turbina isolada termicamente com uma entrada e uma saída de fluxo de ar, não realiza
trabalho técnico, dependendo do fornecimento de energia de um agente externo.
Analisando as afirmações, a equação da 1° Lei pode ser resumida em cada um dos casos.
Indique a/as respostas corretas. Explique sua escolha com relação ao item III
Dicas de solução:
É necessário que o aluno entenda o objetivo de cada aparelho citado. Por exemplo, a válvula em
termos gerais não produz nem consume trabalho. A turbina realiza trabalho técnico. O
compressor consume energia de uma força motriz externa. Ou seja, a única afirmação correta é a
II
8-Vapor de água a 4 MPa entra em uma turbina bem isolada operando em regime permanente
com uma entalpia específica de 3015,4 kJ/kg, e uma velocidade de 10 m/s. O vapor de água se
expande até a saída da turbina onde a pressão é de 0,07 MPa, a entalpia específica é de 2431,7
kJ/kg e a velocidade de 90 m/s.
A vazão mássica é de 11,95 kg/s. Desprezando os efeitos da energia potencial, determine a
potência desenvolvida pela turbina em kW.
9-Ar se expande em uma turbina de 10 bar, 900 K até 1 bar e 500 K. A velocidade na entrada é
pequena, comparada com a velocidade na saída, cujo valor é 100 m/s. A turbina opera em
regime permanente e desenvolve uma potência de 3,2 MW. A transferência de calor entre a
turbina e sua vizinhança, juntamente com os efeitos da energia potencial é desprezível. Calcule a
vazão mássica do ar bem como a área de saída em m2.
10-Ar a 1 bar e com uma entalpia específica de 290 kJ/kg entra em um compressor operando em
regime permanente e sai com uma pressão superior e uma entalpia específica de 1023 kJ/kg. A
vazão mássica é de 0,1 kg/s. Considerando que a potência de entrada do compressor é de 77
KW, determine a transferência de calor entre compressor e sua vizinhança em kW. Despreze os
efeitos das energias cinética e potencial.
Exemplo 4.5 pag. 144 Moram & Shapiro, 6 Edição.
11-Ar é admitido em um compressor que opera em regime permanente com uma pressão de 1
bar, temperatura igual a 290 K e uma velocidade de 6 m/s através de uma entrada cuja área é de
0,1 m2. Na saída a pressão é de 7 bar, a temperatura é de 450 K e a velocidade é de 2 m/s. A
transferência de calor do compressor para sua vizinhança ocorre a uma taxa de 180 kJ/min.
Empregando o modelo de gás ideal, calcule a potência de entrada no compressor em kW
Dicas de solução:
-Aplicar a equação de estado do gás ideal para determinar o volume específico no estado inicial.
-Empregar esse resultado para determinar o fluxo de massa considerando conhecidas no estado
inicial, a velocidade, a área e a densidade (inverso do volume específico). Resultado 0,72 kg/s
-Encontrar as entalpias do ar em função das temperaturas nas tabelas. Para t = 290 K h1 =
290,16 kJ/kg; para T = 450 K, h2 = 451 kJ/kg. (Tabela de entalpias como dado)
-Substituindo os valores na equação de balanço de energia (primeira lei para volumes de
controle), a potência entregue ao compressor é -119,4 kW.
12-Durante um processo de escoamento estacionário, a quantidade total de energia no interior
do volume de controle permanece constante (Ev.c.= constante). Por isso, a quantidade de
energia que entra para o volume de controle nas diferentes formas (calor, trabalho, energia
transportada pela massa) deve ser igual à quantidade total de energia que de lá sai. Para
sistemas com apenas uma corrente de fluido (uma entrada e uma saída), a equação da Primeira
Lei Aplicada a tal volume de controle pode ser expressa como:
.
.
QVC  WVC
2
2
v
v
 m[( hs  he )  ( s  e )  g ( z s  g e )
2
2
.
Representando como índice (s) e índice (e), respectivamente, as propriedades do fluído à saída e
à entrada. Em alguns dispositivos utilizados em engenharia, aplica-se a equação acima e em sua
maioria, há a possibilidade de algumas considerações serem feitas e também alguns
cancelamentos. Com relação às proposições abaixo, é incorreto afirmar que:
a) Uma turbina é um dispositivo onde se produz trabalho resultante da passagem de um gás, ou
líquido, através de um conjunto de lâminas presas a um eixo que pode girar. Normalmente, e em
particular nas turbinas de gás e vapor, a variação de energia potencial gravitacional do fluido é
desprezível.
b) Numa bomba fornece-se trabalho a um líquido para lhe modificar o estado enquanto este a
atravessa. As trocas de calor com a vizinhança são, normalmente, pouco significativas, podendo
o termo Qv.c. ser cancelado e o trabalho fornecido ao fluido, por convenção, deve ser negativo.
c) Um bocal é um dispositivo usado para diminuir a velocidade do escoamento de um fluido,
reduzindo a pressão. Não há trabalho adicionado nesses dispositivos e, normalmente, a
transmissão de calor é ignorada.
d) Os trocadores de calor são usados para transmitir energia de um corpo mais quente para um
mais frio ou para a vizinhança por transmissão de calor. Nestes dispositivos, a velocidade
normalmente muda pouco, a queda de pressão através da passagem é ignorada na transmissão
de calor, a variação de energia potencial é assumida como zero e também não há trabalho
realizado.
.
.
2
.
QVC  WVC  m[( hs  he )  (
.
.
.
2
cs
c
 e )  g ( z s  ze )
2
2
0  QVC  WVC   me (he 
2
2
.
ce
c
 g e )   m s (hs  s  g s )
2
2
É incorreto afirmar item c.
13-Um aquecedor de água de alimentação opera em regime permanente com água líquida
escoando, ao longo da entrada 1, a 50 kPa, 40°C e com uma vazão mássica de 70 kg/s. Um fluxo
de água separada penetra na entrada 2 com uma mistura bifásica líquido-vapor a 50 kPa com um
título de 98%. Líquido saturado a 50 kPa sai do aquecedor de água de alimentação por 3.
Ignorando a transferência de calor para a vizinhança e desprezando os efeitos das energias
cinéticas e potenciais, determine a vazão mássica do líquido saturado na saída do aquecedor,
em kg/s.