i) Calcule a matriz de confusão do classificador A.

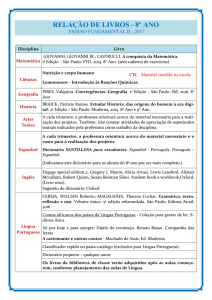
Engenharia Informática (ramos de Gestão e Industrial)
Reconhecimento de Padrões
1ª Série de Problemas
Classificação de dados
Realizado por: Prof. João Ascenso.
Departamento de Sistemas e Informática
Data: 09/10/04
1
Exercícios de classificação de dados
1.1
Dado um classificador A, foi realizada a seguinte experiência de classificação:
X
1
2
3
4
5
6
7
8
9
w
1
2
1
1
2
2
3
2
2
west
2
2
1
2
2
3
2
3
1
i) Calcule a matriz de confusão do classificador A.
ii) Calcule a probabilidade de erro do classificador, assumindo que o vector de
probabilidades à priori é [1/5, 2/5, 2/5].
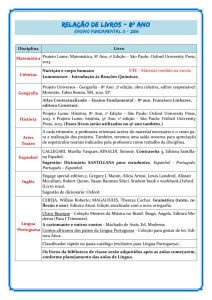
1.2 Seja ζ: {A, B, C, D}→{w1, w2, w3} um classificador definido pelas funções
discriminantes descritas na seguinte tabela:
A
B
C
D
g1
1
2
0
-2
g2
0
3
2
0
g3
-1
1
-1
1
i) Determinar as regiões de classificação
ii) A tabela seguinte contém uma sequência dos padrões de teste, para os quais se conhece
a classe correcta. Classifique os padrões, construa a matriz de confusão do classificador e
obtenha a probabilidade de erro.
X
B
C
A
A
B
C
A
B
C
C
D
w
1
2
1
1
2
2
3
2
2
3
3
1.3 Classifique as observações 1.2, 5.6 e -2 utilizando as seguintes funções
discriminantes:
i) g1 (x)  x 2  1; g2 (x)  7  2 x
1
2
ii) g1 (x)   x  3 ; g 2 (x)  x  1; g 3 (x)  3.(x  3 )
1.4 Determine as regiões de decisão dos classificadores definidos pelas seguintes
funções:
i) g1 (x)  x  4; g2 (x)  2 x  5
ii) g1 (x)  2 x 2  1; g2 (x)   x 2  4 x
iii) g1 (x)  log(x 2  3 ); g2 (x)  log 12
1.5 Suponhamos duas classes ω1 e ω 2 , e um vector unidimensional X . As funções de
verosimilhança para as duas classes são:
p(x | ω1 ) 
1 (x 2 )2
e
2π
p(x | ω2 ) 
2
2
1
e (x 4 ) 8
2 2π
Dado que p(ω1 )  1 2 e p(ω2 )  1 2 , diga qual é o erro de classificação mínimo (critério
de MAP) e o erro de classificação correspondente.
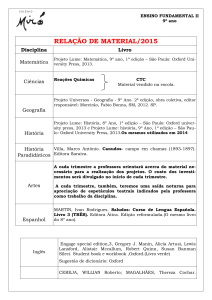
1.6 Seja x  {a, b, c} uma observação aleatória produzida pela classe w = {w1, w2, w3}
com uma distribuição definida na seguinte tabela:
P(x | wi)
a
b
c
w1
0.4
0.4
0.2
w2
0.1
0.6
0.3
w3
0.3
0
0.7
Com P(w1) = 0.3, P(w2) = 0.6, P(w3) = 0.1
i) Calcule as regiões de decisão para o classificador MAP (Máximo À Posteriori)
ii) Calcule a probabilidade de erro
1.7
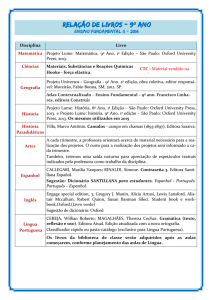
Para um problema de 2 classes unidimensionais temos duas acções possíveis:
i) a1 – escolha w1 ii) a2 – escolha w2 e a seguinte função de custo:
A
B
g1
¼
0
g2
0
¼
as seguintes distribuições:
P(x | w1) = e-x (x >0)
1
0≤x≤1
2

P(x | w2) =  e  x
 e  2( x 1) 1 < x < ∞

 2
i)Calcule a razão de verosimilhança e as regiões de decisão
ii)Calcule o risco de Bayes
1.8 Encontrar a transformação Y = AX que transforme a distribuicão normal N(0,1)
em N(μ, Σ) em que μ corresponde á média e Σ corresponde á covariância.
1.9 Seja x uma observação gerada por 1 de 2 classes equiprováveis ω1 e ω2 e sabendo
que cada uma das classes gera observações com distribuição normal N(μi, 1) com μ1 ≥ μ2
calcule:
i)um classificador MAP.
ii)regiões de decisão do classificador.
iii)repita as duas alíneas anteriores para as distribuições normais N(0, σi) com σ1 ≥ σ2 .
1.10 Seja x uma variável aleatória gerada por 1 de duas classes ω1 , ω2 com as seguintes
distribuições:
P(x |ω1 ) = N(-1, 2) e P(x |ω2 ) = N(1, 1/2)
e as probabilidades à priori P(ω1 ) = 0.7 e P(ω2 ) = 0.3 e a seguinte matriz de risco:
0 1
R 
.
4 0
i) Calcule para o classificador de Bayes as regiões de decisão.
1.11 Considere o classificador de Bayes para classes com distribuição normal,
 1 0
1
3
1
i     2  , i 1,2,3 com 1    , 2    , 3   
 0 1
1
1
3
com probabilidades á priori iguais: P 1   P 2   P 3  .
Calcule as funções discriminantes.
1.12 Considere o classificador de Bayes para classes com distribuição Normal,
0 
 2
 2
 2
2
1    , 2    , 3    , 4    , 5    com i     2 I
0 
0
0
2
 2
e com probabilidades á priori iguais: P 1   P 2   P 3   P 4   P 5 
Desenhe as regiões de decisão segundo o critério MAP.
1.13 Considere o seguinte problema de classificação em duas classes dos seguintes
padrões:
x1 = [1, 0.9],
x2 = [2.5, 1.6],
x3 = [1.5, 0.5]
Assuma que os dados obedecem a distribuições Gaussianas bivariadas com média igual a
[1, 1] e [2, 0], respectivamente e covariância igual à matriz de identidade. Admita que as
classes são equiprováveis.
i) Determine a regra de decisão MAP identificando um conjunto de funções
discriminantes.
ii) Determine as regiões de decisão do classificador.
iii) Classifique as amostras x1, x2 e x3 segundo o classificador de MAP. Indique a
respectiva probabilidade de erro.
iv) Admita que as classes têm probabilidade à priori diferentes. De que forma tal facto iria
influenciar as regiões de decisão ? Explique como. Desenhe gráficos apropriados para
cada um dos casos.