Coordenadas_verticais

Adilson W. Gandu - DCA/IAG/USP
Document1
COORDENADAS VERTICAIS
Referência: Kasahara A, 1974: Various vertical coordinate systems used for numerical
weather prediction. Monthly Weather Review, 102, 509-522.
 Nos modelos atmosféricos, diversos tipos de coordenadas verticais têm sido usados,
conforme a aplicação do modelo. Todos os tipos de coordenadas verticais têm certas
vantagens e desvantagens. Alguns desses tipos serão apresentados abaixo:
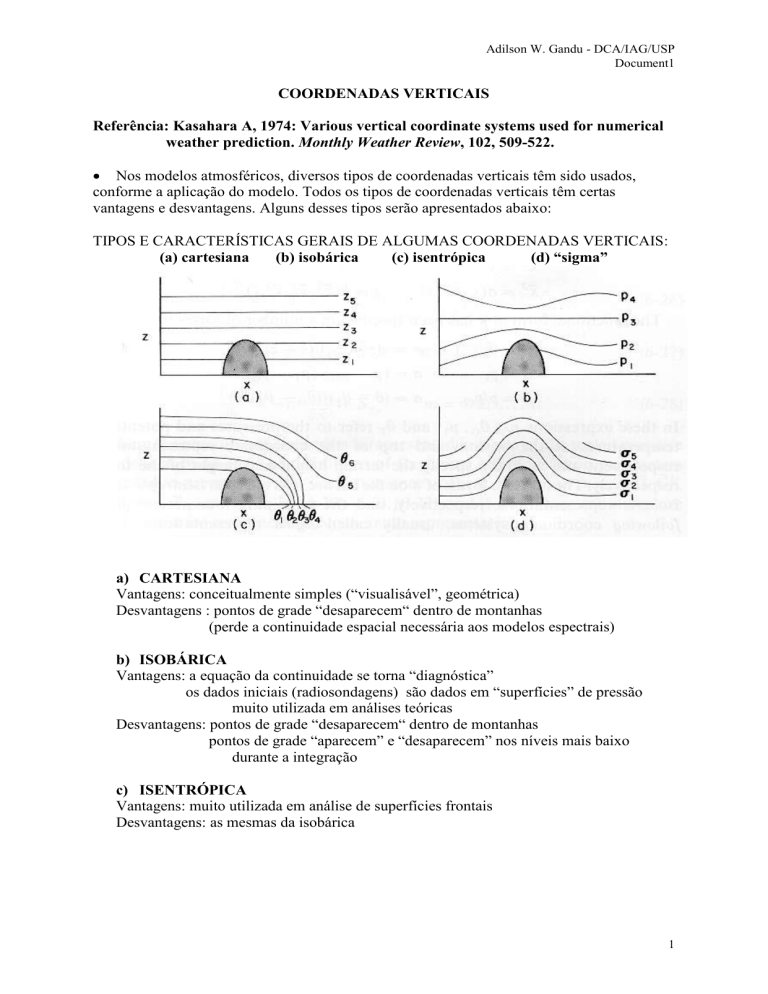
TIPOS E CARACTERÍSTICAS GERAIS DE ALGUMAS COORDENADAS VERTICAIS:
(a) cartesiana
(b) isobárica
(c) isentrópica
(d) “sigma”
a) CARTESIANA
Vantagens: conceitualmente simples (“visualisável”, geométrica)
Desvantagens : pontos de grade “desaparecem“ dentro de montanhas
(perde a continuidade espacial necessária aos modelos espectrais)
b) ISOBÁRICA
Vantagens: a equação da continuidade se torna “diagnóstica”
os dados iniciais (radiosondagens) são dados em “superfícies” de pressão
muito utilizada em análises teóricas
Desvantagens: pontos de grade “desaparecem“ dentro de montanhas
pontos de grade “aparecem” e “desaparecem” nos níveis mais baixo
durante a integração
c) ISENTRÓPICA
Vantagens: muito utilizada em análise de superfícies frontais
Desvantagens: as mesmas da isobárica
1
Adilson W. Gandu - DCA/IAG/USP
Document1
d) “SIGMA”

p
  
 (Phillips, 1957)
ps 

Vantagens: “seguem” o terreno, sem interceptá-lo
muito utilizado
Desvantagens: grandes erros no cálculo da força do gradiente de pressão ( “ETA”)
COORDENADA VERTICAL GENERALIZADA (s)

Seja uma variável dependente “A” qualquer, função das variáveis independentes
(cartesianas) “x”, “y”, “z”, e “t” :
A  A x, y, z , t 

Assume-se que exista uma variável “s” que também seja função de “x”, “y”, “z”, e
“t”, e que essa função dá uma relação monotônica (de valor único) entre “s” e “z”:
s  s  x, y , z , t 
e, portanto,
z  z  x, y , s , t 
s constante
z constante

Assim, a variável “A” pode ser escrita como:
A  Ax, y, s x, y, z , t , t 
e sua derivada vertical como:
A
A s

z
s z
(1)
2
Adilson W. Gandu - DCA/IAG/USP
Document1

QUESTÕES: Como ficam nas equações básicas da atmosfera,
- os gradientes horizontais (em especial a força do gradiente de pressão) ?
- a derivada total ?
- a “velocidade” vertical nessa coordenada ?
- a divergência ?

As derivadas parciais de A em relação a “x”, “y” e “t”, com “s” constante:
A  Ax, y, z  x, y, s, t , t 

A  z 
 A 
 A 
     
  , ou, usando a equação (1):
z  x  s
 x  s
 x  z
Como
A s  z 
 A 
 A 


 
 
 
s z  x  s
 x  s
 x  z
(2)
Similarmente, para “y” e “t”:
 A 
 A 
A s  z 
     
 

y

y

s

z
 s
 z
 y  s
(3)
A s  z 
 A 
 A 
     
 

t

t

s

z
 s
 z
 t  s
(4)
I – GRADIENTE HORIZONTAL na coordenada “s”

Somando-se (2) e (3):
s  A
s A   z A 
s z
z
s



(5)
Por exemplo, a aceleração devido a Força do Gradiente de Pressão no sistema de
coordenada “s” fica:
1 
s 
p 
  z p    s p 
s z 

 
z
s 
1

3
Adilson W. Gandu - DCA/IAG/USP
Document1

Mas, da equação (1), fazendo A  p:
p
p s

z
s z
p
  g ,
z
ou, usando a equação hidrostática
p
  g
s
s
z
que, substituindo na equação acima resulta em:

1


z p  
1



s p  g s z
(6)
Observar que no sistema de coordenada “s”, a aceleração devido à FGP é resultado da soma
de dois termos.
II – DERIVADA TOTAL e “VELOCIDADE” VERTICAL em “s”

A derivada total da variável “A” em coordenada “z” pode ser escrita como
 
dA
A
 A 
    V  z A  w
dt
z
 t  z

Substituindo a derivada temporal de “A” pela equação (4), o gradiente horizontal
de “A” em z constante pela equação (5), e a derivada vertical de “A” pela
equação (1), resulta em:
4
Adilson W. Gandu - DCA/IAG/USP
Document1
 A 
dA
s  z  A  
   
 V
 

dt
z  t  s s 
 t  s
A s
 w
s z


s


s A  s z

z

Agrupando os termos que contem “s/z”, e rearranjando, obtem-se:
 
 

dA  A 
 z 
    V   s A  w     V   s
dt
 t  s
 t  s



s 
assim como

 s A
z
 z s
Mas, por definição, a derivada total em “s” é:


 A
dA
 A 
    V  s A  s
dt
s
 t  s
onde
 A 
 
 s 
ds
dt
(7)
é a “velocidade” vertical na coordenada “s”,
w 
dz
dt
é a velocidade vertical na coordenada “z”.
Como as duas expressões anteriores para a derivada total de “A” são iguais,
comparando-as obtemos então a relação entre as velocidades verticais nessas duas
coordenadas:
s
s 
z

 

 z 
w   t   V   s
 s


z

(8)
5
Adilson W. Gandu - DCA/IAG/USP
Document1
III – DIVERGÊNCIA HORIZONTAL em “s”

Em coordenada “z”, a divergência pode ser escrita como:
 v 
 u 
z  V      
 x  z  y  z



Utilizando as equações (2) e (3), a divergência em “s” fica:



V
 s  
s  V   z  V    s z 
s 
 z  






(9)
IV – GRADIENTE VERTICAL DE “w” em “s”

Termo necessário para a equação da continuidade:


d
ln     z  V  w  0
dt
z

Da equação (1)
w
w s

z
s z

Para avaliar o primeiro termo da lado direito dessa equação, “w” é substituído
pela equação (8), que relaciona as velocidades verticais nos sistemas “z” e “s”:
w
  z  
  

V  s
  
s
s  t  s  s 
   z 

z 
s 


s

 s 
6
Adilson W. Gandu - DCA/IAG/USP
Document1

“Abrindo” os termos dessa equação:


 
w
  z   V
 z   s z
 z 

 s z  V  s   
 s
  
 
s
t  s 
s

s

s

s

s
 
 s 



Por outro lado, os termos envolvendo “z/s” pode ser reagrupados como

t


 z     z   
   V  s    s
s
 s 
 s 
d
 z 

 
dt
 s 
 z 
 
 s 
Assim, o gradiente vertical de “w” pode ser reescrito como:


w
d  z   V
 s  z 

 s z 
  
 
s
dt  s 
s
s  s 


Portanto

w
w s
s  d


z
s z
z  dt




s
 z   V
 s z 
  
s
s

 s 


(10)
7
Adilson W. Gandu - DCA/IAG/USP
Document1
RESUMO
EQUAÇÕES PRIMITIVAS em coordenadas “z” e “s”
EQUAÇÃO DO MOMENTO HORIZONTAL
 Em “z”

 

dV
1 
 f k  V    z p  F atrito
dt


onde:


V  u i v j

   
z 
 j
 i
x  z
y  z
 
d



 V  z  w
dt
t
z
,
w 
dz
dt
 Em “s”

 


dV
1 
 f k  V    s p  g  s z  F atrito
dt

   
s 
 j
 i
x  s
y  s
 
 
d


 V  s  s
dt
t
s

onde:

,
s 
ds
dt
8
Adilson W. Gandu - DCA/IAG/USP
Document1
EQUAÇÃO HIDROSTÁTICA
 Em “z”
p
  g
z
 Em “s”

z
1 p
 
s
g s
EQUAÇÃO TERMODINÂMICA
 Em “z” e “s”

dT
dp
cp

 q
dt
dt
OBS.: só muda a forma da derivada total
EQUAÇÃO DA CONTINUIDADE
 Em “z”


d
ln     z  V  w  0
dt
z
 Em “s”
d
dt

s
  z 
ln




V

 0
s
  s 
s




9
Adilson W. Gandu - DCA/IAG/USP
Document1
MOVIMENTO VERTICAL
s
s 
z

 

 z 
w   t   V   s
 s


z

DIVERGÊNCIA HORIZONTAL



s 
V
s  V   z  V 
s z 
z 
s 






10