Trabalho1ano - Instituto Montessori

Instituto Montessori - Ponte Nova
Atividades – 1ª série E.M. – 2º trimestre
01 - (UFPE/2011)
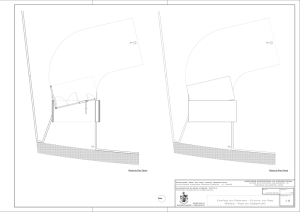
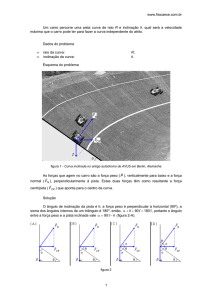
Na ilustração abaixo, temos dois retângulos congruentes com base medindo 12 cm, e altura 5 cm.
Qual o inteiro mais próximo da distância, em cm, do ponto A até a horizontal? Dado: use a
aproximação 3  1,73.
02 - (ESPM SP/2011)
Um reservatório de água é constituído por uma esfera metálica oca de 4 m de diâmetro, sustentada
por colunas metálicas inclinadas de 60º com o plano horizontal e soldadas à esfera ao longo do seu
círculo equatorial, como mostra o esquema abaixo.
Sendo
a)
b)
c)
d)
e)
3  1,73 ,
a altura h da esfera em relação ao solo é aproximadamente igual a:
2,40 m
2,80 m
3,20 m
3,40 m
3,60 m
03 - (UNIFOR CE/2011)
O Edifício Joelma tornou-se conhecido nacional e internacionalmente quando, em fevereiro de
1974, um incêndio provocou a morte de 188 pessoas. Foi inaugurado em 1971 e continha vinte e
cinco andares, sendo dez de garagens. Hoje é denominado Edifício Praça da Bandeira. Suponha
que cada andar tem 2 metros de altura e um carro de bombeiro tenha se posicionado em frente ao
prédio incendiado. Se a inclinação máxima da escada é 30° e o seu tamanho máximo é 60m, qual
será o último andar alcançado pela escada?
(Imagem disponível em: www.rived.mec.gov.br.
Acesso em: 01/11/2010.)
a)
b)
c)
d)
e)
5º Andar.
7º Andar.
8º Andar.
10º Andar.
15º Andar.
04 - (UNESP SP/2011)
Uma pessoa se encontra no ponto A de uma planície, às margens de um rio e vê, do outro lado do
rio, o topo do mastro de uma bandeira, ponto B. Com o objetivo de determinar a altura h do
mastro, ela anda, em linha reta, 50 m para a direita do ponto em que se encontrava e marca o
ponto C. Sendo D o pé do mastro, avalia que os ângulos BÂC e BĈD valem 30º, e o ângulo AĈB
vale 105º, como mostra a figura.
A altura h do mastro da bandeira, em metros, é
a)
b)
c)
d)
e)
12,5.
12,5
25,0.
25,0
35,0.
2
.
2
.
05 - (UFAL/2011)
De um ponto A, situado no mesmo nível da base de uma torre, o ângulo de elevação do topo da
torre é de 20°. De um ponto B, situado na mesma vertical de A e 5m acima, o ângulo de elevação
do topo da torre é de 18º.
Qual a altura da torre? Dados: use as aproximações tg 20°  0,36 e tg 18°  0,32.
a)
b)
c)
d)
e)
42m
43m
44m
45m
46m
06 - (ENEM Simulado/2009)
Uma empresa precisa comprar uma tampa para o seu reservatório, que tem a forma de um tronco
de cone circular reto, conforme mostrado na figura.
Considere que a base do reservatório tenha raio r  2 3m e que sua lateral faça um ângulo de 60º
com o solo.
Se a altura do reservatório é 12m. a tampa a ser comprada deverá cobrir uma área de
a) 12 m2
b) 108 m2
c) (12  2 3 ) 2  m 2
d) 300 m2
e) ( 24  2 3 ) 2  m 2
07 - (FUVEST SP/2006)
Na figura abaixo, a reta s passa pelo ponto P e pelo centro da circunferência de raio R,
interceptando- a no ponto Q, entre P e o centro. Além disso, a reta t passa por P, é tangente à
circunferência e forma um ângulo  com a reta s. Se PQ = 2R, então cos vale
a)
b)
c)
d)
e)
2 /6
2 /3
2 /2
2 2 /3
3 2 /5
08 - (UEM PR/2006)
Uma esteira rolante de um supermercado com dois andares faz um ângulo de 30º com o plano
determinado pelo piso inferior. Assinale o que for correto, considerando o comprimento da esteira
12 metros.
a) Uma pessoa que sai do piso inferior e vai ao piso superior se eleva 6 (seis) metros.
b) Faltam dados para se calcular a altura total que uma pessoa se eleva ao ir do piso inferior ao
piso superior utilizando a esteira.
c) Se uma pessoa caminha 2 metros na esteira durante o percurso entre o piso inferior e o piso
superior, então a pessoa se eleva, no total, 5 (cinco) metros.
d) Uma pessoa que sai do piso inferior e vai ao piso superior se eleva 6 3 metros.
e) Se uma pessoa caminha 2 metros na esteira durante o percurso entre o piso inferior e o piso
superior, então a pessoa se eleva, no total, 5 3 metros.
09 - (MACK SP/2005)
Na figura, quaisquer que sejam  e , sen é sempre igual a:
a) cos 
b) sen 2
c) sen 2
d) cos 
e) cos 2
10 - (UFPR/2005)
Calcule o seno do maior ângulo de um triângulo cujos lados medem 4, 6 e 8 metros.
15
4
a)
b)
c)
d)
1
4
1
2
10
4
e)
3
2
11 - (UFG GO/2004)
Segundo as normas de segurança, balanços pendurados em barras horizontais, com uso de
correntes, devem manter uma distância lateral, de modo a permitir uma inclinação lateral com
segurança. Considere um balanço na posição vertical e um outro com uma inclinação lateral de
30º, em que essa inclinação é tal que, para qualquer inclinação menor, os balanços não se tocam, e
para uma inclinação maior ou igual eles se tocam, conforme a figura abaixo.
d
30º
Considerando que o comprimento das correntes desses balanços seja 2 metros, calcule a distância d
entre eles.
12 - (UFPE/2003)
Dois pavimentos de uma construção devem ser ligados por uma escada com 10 degraus de mesma
altura, construída sobre uma rampa de 3,6m como ilustrado na figura abaixo. Se sen  = ½,
indique a altura, em centímetros, de cada degrau.
3,60

13 - (UNESP SP/2003)
Numa fábrica de cerâmica, produzem-se lajotas triangulares. Cada peça tem a forma de um
triângulo isósceles cujos lados iguais medem 10 cm, e o ângulo da base tem medida x, como
mostra a figura.
a) Determine a altura h(x), a base b(x) e a área A(x) de cada peça, em função de senx e cosx.
b) Determine x, de modo que A(x) seja igual a 50 cm2.
14 - (UFU MG/2001)
Considerando que na figura abaixo BC = 2cm, a área do triângulo eqüilátero ABD é igual a
D
12
0
6
0
3
0
A
a)
b)
c)
d)
B
C
3
cm 2
3
2
3 3cm
3cm 2
3
cm 2
2
15 - (UEL PR/2001)
Com respeito aos pontos A, B, C, D e E, representados na figura abaixo, sabe-se que CD = 2.BC e
que a distância de D a E é 12m. Então, a distância de A a C, em metros, é:
B
A
60º
C
30º
D
E
a)
b)
c)
d)
e)
6
4
3
2
1
16 - (UNIFOR CE)
O losango ABCD tem seus quatro vértices localizados sobre os eixos cartesianos, como mostra a
figura abaixo.
y
B
C
A
x
D
Se seus ângulos internos medem 60º e 120º e sua diagonal maior mede 8 cm, então o ponto B é o
ponto
a)


0; 3 
 2 


b)
2 3


; 0
 3



c)
 2 3
0 ;



3


d)
4 3


; 0
 3



e)
 4 3
0;


3 

17 - (UFG GO)
Um ponto P, interno a um ângulo, cuja medida é 75º, dista 2cm de um dos lados do ângulo e 4cm
do vértice do ângulo. Qual é a distância desse ponto ao outro lado do ângulo?
18 - (VUNESP SP)
Duas rodovias retilíneas A e B se cruzam formando um ângulo de 45º. Um posto de gasolina se
encontra na rodovia A, a 4km do cruzamento. Pelo posto passa uma rodovia retilínea C,
perpendicular à rodovia B. A distância do posto de gasolina à rodovia B, indo através de C, em
quilômetros, é
a) 82
b)
2
4
c)
3
2
d)
e)
2
2 2
19 - (UNIFICADO RJ)
Na figura abaixo, ABCD é um trapézio retângulo com
Então:
A
AB  AD ,
BC – AB = 1 cm e CD = 7 cm.
B

a)
b)
c)
d)
e)
sen  = 1/3
sen  = 3/5
cos  = 4/5
tg  = 3/4
tg  = 4/3
D
C
20 - (UNIRIO RJ/1996)
Um disco voador é avistado, numa região plana, a uma certa altitude, parado no ar. Em certo
instante, algo se desprende da nave e cai em queda livre, conforme mostra a figura.
A que altitude se encontra esse disco voador?
^

d
Considere as afirmativas:
I- A distância d é conhecida;
II- A medida de ̂ a tg ̂ são conhecidas.
Então, tem-se que:
a) a I sozinha é suficiente para responder à pergunta, mas a II, sozinha, não.
b) a II sozinha é suficiente para responder à pergunta, mas a I sozinha, não.
c) I e II, juntas, são suficientes para responder à pergunta, mas nenhuma delas, sozinha, o é.
d) ambas são, sozinhas, suficientes para responder à pergunta.
e) a pergunta não pode ser respondida por falta de dados.
21 - (FUVEST SP)
Calcular x indicando na figura.
x
30°
60°
100m
22 - (MACK SP)
Na figura abaixo determinar o valor AB.
A
30°
50
60°
B
23 - (UNIFOR CE/2010)
Calcule o perímetro do triângulo retângulo ABC, mostrado na figura ao lado, sabendo-se que o
segmento BC mede 10m e cos   3 .
5
a) 24m
b) 26m
c) 28m
d) 32m
e) 36m
24 - (FGV /2010)
A figura ilustra as medidas que um topógrafo tomou para calcular a distância do ponto A a um
barco ancorado no mar.
sen62º = 0,88; cos62º = 0,47
sen70º = 0,94; cos70º = 0,34
a) Use os dados obtidos pelo topógrafo e calcule a distância do ponto A ao barco. É conveniente
traçar a altura AH do triângulo ABC.
b) Use esses mesmos dados para calcular o valor de cos48º. Se quiser, utilize os produtos: 8894
= 8272 e 4734 = 1598.
25 - (UFSM RS/2010)
Entre os pontos A e C, localizados na margem de um lago, será estendido um cabo com boias
sinalizadoras que demarcará a parte permitida para o passeio de pedalinhos. Para a compra do
material a ser utilizado, é necessário determinar a distância entre esses pontos.
A medição direta da distância entre A e C não pode ser realizada, pois fica sobre a superfície do
lago. Assim, marcou-se um ponto B intermediário, de modo que as distâncias entre A e B e entre B
e C pudessem ser feitas sobre terra firme.
Sabendo que a distância entre A e B é 100 metros, que a distância entre B e C é 60 metros e que o
ângulo com vértice em B determinado por A, B e C é 120 graus, a distância entre A e C, em
metros, é
a)
b)
c)
d)
e)
120.
140.
150.
155.
160.