Exp5_CEEProjeto_de_Trafo_mono_II

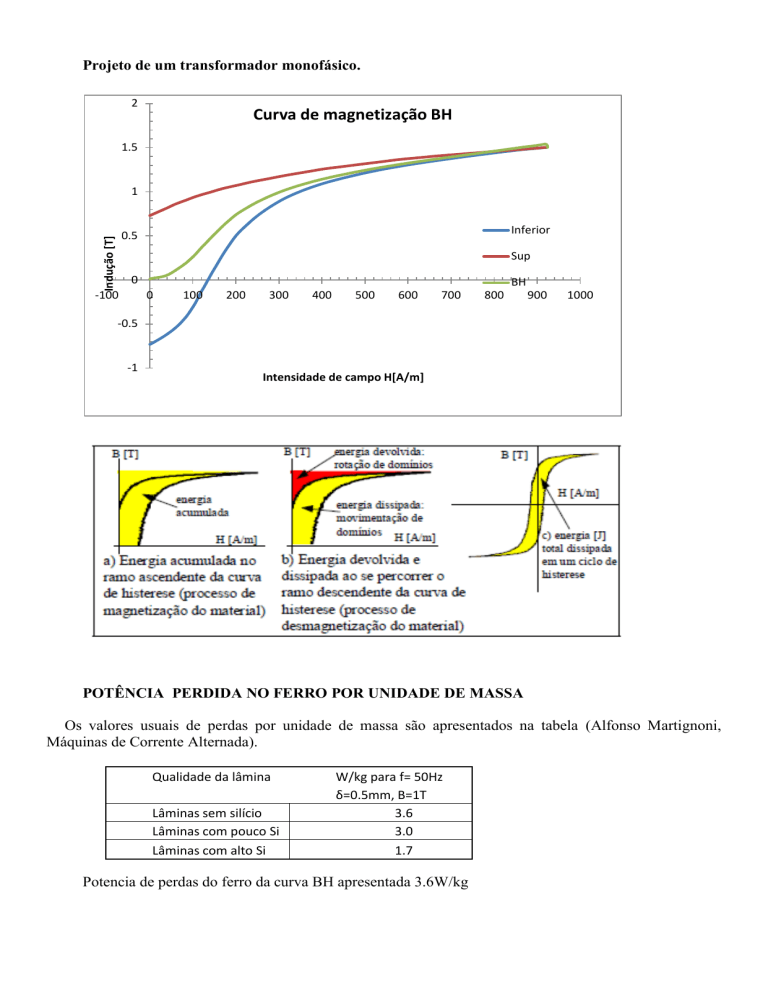
Projeto de um transformador monofásico.
2
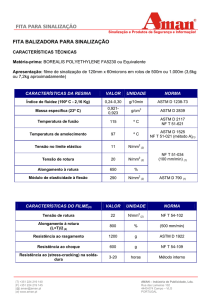
Curva de magnetização BH
1.5
Indução [T]
1
Inferior
0.5
Sup
0
-100
BH
0
100
200
300
400
500
600
700
800
900
1000
-0.5
-1
Intensidade de campo H[A/m]
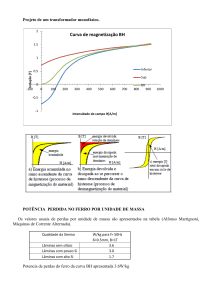
POTÊNCIA PERDIDA NO FERRO POR UNIDADE DE MASSA
Os valores usuais de perdas por unidade de massa são apresentados na tabela (Alfonso Martignoni,
Máquinas de Corrente Alternada).
Qualidade da lâmina
Lâminas sem silício
Lâminas com pouco Si
Lâminas com alto Si
W/kg para f= 50Hz
δ=0.5mm, B=1T
3.6
3.0
1.7
Potencia de perdas do ferro da curva BH apresentada 3.6W/kg
POTÊNCIA ATIVA POR UNIDADE DE MASSA
Através da curva BH e a operação em condição acumulativa foi possível determinar a energia
acumulada sobre o volume de ferro, esta energia acumulada por ciclo permite o cálculo da potência máxima
do dispositivo.
Como é conhecido o volume e a densidade do material é possível determinar a potência máxima
associada à unidade de volume e de massa, neste caso para um volume de 0.000142738m3 (você utiliza o
do seu trafo)
Exemplo:
Potência por volume = 50W/0.000142738m3 = 370Kw/m3
Peso do transformador = 7900 Kg/m3* 0.000142738m3 = 1.14Kg
Potência por Kg =50 W/1.14g = 46.5W/Kg
A densidade típica do ferro é de 7900Kg/m3, variando levemente segundo a liga formada.
Corrente associada as perdas Ir
P
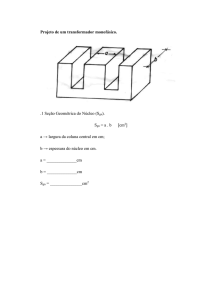
.1 Seção Geométrica do Núcleo (Sgn).
Sgn = a . b
a → largura da coluna central em cm;
b → espessura do núcleo em cm.
[cm2]
V2
V
 Ir 
Rp
Rp
a = ______________cm
b = ______________cm
Sgn = _______________cm2
.2 Seção Magnética do Núcleo (Smn),
Smn = Sgn . Fu [cm2]
Sgn → Seção Geométrica do Núcleo;
Fu → Fator de utilização. Número que varia entre 0,8 e 0,9, dependendo do estado de conservação das
chapas.
Sgn = ______________________cm2
Fu = ________________
Smn = _____________________cm2
Cálculo do numero de espiras e corrente de magnetização
Da curva BH , para uma indução de 1[Teslar] ( valor adotado freqüentemente nos projetos de
transformadores) corresponde uma intensidade de campo H de 350 [Ae/m]
Numero de espiras primarias se secundarias
Da lei de faraday
Considerando um fluxo magnético senoidal  (t )   m sent , a expressão para a tensão de pico
correspondente à tensão V1 rms, é dada por:
Epk = N
d
dt
=> 2V1  Nm cos t
Na condição de valor maximo =>
=>
2V1  N (S mn B) cos t
2 * 220  N (S mn B)2f
Primario
Secundário
V  108
1
N1 
4,44  f  B  S
V  108
2
N2 
4,44  f  B  S
mn
mn
Da lei de Amper
Percurso médio das linhas de fluxo lm=0.01686[m]
H*lm=Ni => i=
350[ Ae / m] * l m [m]
 I m = Corrente de magnetização,
N1[e]
Corrente de vazio
A corrente de vazio corresponde a soma fasorial das correntes originadas pelas perdas do ferro e a de
magnetização
Io= Ir + Im
Corrente para a simulação
Fluxo acumulativo
Fluxo Diferencial
Trafo CEE 2
28 AWG
[primario:1100]
Air
28 AWG
[primario:-1100]
22 AWG
[secundario:120]
22 AWG
[secundario:-120]
Trafo CEE 2
TRIÂNGULO DE POTÊNCIAS
Na simulação se obteve a perda do ferro de P fe = 3.6 e as perdas do cobre Pcu = 3.1W. (condição de projeto
ótima Pfe~Pcu). Obtendo um rendimento de:
Potência Total= Potência calculada no gráfico BH + Potência das perdas Pfe~Pcu = 50 + 3.0+3.1= 56
 = [50)]/56 = 0.90
Potência ativa: P1= 56[W] (obtida a partir das características magnéticas curva BH)
Potência Reativa
Q1= VI m [VAR]
Potência aparente: S1= I1* V1 =
P12  Q12
Fator de potência FP
3 Potência do Núcleo ou Potência do Primário (S1).
S1 ……………. [VA]
Smn → Seção magnética do núcleo (cm2)
Smn = ______________________cm2
S1 = ____________________VA
4 Potência do Secundário (S2).
A potência do secundário é inferior a potência do primário, devido às perdas internas no
transformador.
S2 =
S
1 [VA]
1,10
S1 → Potência do Primário (VA);
S1 = ____________________VA
S2 = ____________________VA
1,10 → constante provenientes das perdas internas no transformador.
5 Corrente do Primário (I1).
S1= I1 V1 =
P12  Q12
S1 → Potência do primário (VA);
V1 → Tensão do primário (V).
Observação: Quando o enrolamento primário possuir mais de uma tensão, devemos calcular a corrente
correspondente a cada tensão.
Exemplo: se o transformador for o abaixo.
Teremos:
I1 =
S1
220
e
I1 =
S
1
127
S1 = _________________VA
V1 = _________________V
I1 = __________________A
6 Corrente do Secundário (I2)
P12  Q12
S2= I2 V2 =
1.1
S2 → Potência do secundário (VA);
V2 → Tensão do secundário (V).
Observação: Quando o enrolamento secundário possuir mais de uma tensão, devemos calcular a
corrente correspondente a cada tensão.
Exemplo: se o transformador for o anteriormente usado, teremos.
S
I2 =
2
12
S
e
I2=
2
24
S2 = ____________________VA
V2 = ____________________V
I2 = _____________________A
7 Seção do Fio do Enrolamento Primário (S1c).
I
S1c = 1
d
[mm2]
I1 → Corrente do enrolamento primário (A);
d → Densidade de corrente (A/mm2), escolher-se-á um valor entre os limites de 3 a 6 A/mm2.
S1c → Seção calculada do enrolamento primário (mm2);
S1r → Seção real do enrolamento primário, obtida mediante consulta a tabela de fios anexa (procurar o
valor mais próximo).
Observação: Quando o enrolamento primário possuir mais de uma tensão, logo, mais de uma corrente,
devemos calcular as diversas seções existentes no enrolamento. Exemplo: se considerarmos o transformador
usado anteriormente, teremos.
I
S1c = 1
d
I1= __________________A
d = __________________A/mm2
S1c = __________________ mm2
S1r = __________________mm2
8 Seção do Fio do Enrolamento Secundário (S2c).
I
S2c = 2 [mm2]
d
I2 → Corrente do enrolamento secundário (A);
d → Densidade de corrente (A/mm2), escolher-se-á um valor entre os limites de 3 a 6 A/mm2.
S2c → Seção calculada do enrolamento secundário (mm2);
S2r → Seção real do enrolamento secundário, obtida mediante consulta a tabela de fios anexa (procurar
o valor mais próximo).
I2 = ____________________A
d = ____________________A/mm2
S2c = ___________________mm2
S2r = ___________________mm2
9 Densidade Real de Corrente do Primário (dr1).
dr1 =
I
1
S
1r
[A/mm2]
I1 → Corrente do enrolamento primário (A);
S1r → Seção real do fio do enrolamento primário (mm2);
dr1 → Densidade real (A/mm2) e deve ficar entre os limites de 3 a 6 A/mm2.
Observação: Quando o enrolamento primário possuir mais de um valor de tensão, logo, mais de um
valor de corrente devemos calcular todas as densidades correspondentes, tendo então.
dr1=
I
1
S
1r
I1 = ___________________A
S1r = __________________mm2
dr1 = __________________A/mm2
.10 Densidade Real de Corrente do Secundário (dr2).
I
dr2 =
S
2
[A/mm2]
2r
I2 → Corrente do enrolamento secundário (A);
S2r → Seção real do fio do enrolamento secundário (mm2);
dr2 → Densidade real (A/mm2) e deve ficar entre os limites de 3 a 6 A/mm2.
I2 = ___________________A
S2r = __________________mm2
d2r = __________________A/mm2
11 Número de Espiras do Enrolamento Primário (N1)
V  108
1
N1 =
4,44  f  B  S
[espiras]
mn
V1 → Tensão do enrolamento primário (V);
f → Freqüência (60 Hz);
B → Indução magnética, valor entre 10.000 e 11.000 Gauss.
Observação: Se as chapas do núcleo forem de boa qualidade usa-se B= 11.000 Gauss, caso contrário
B= 10.000 Gauss. Se o enrolamento primário possuir outras tensões, podemos determinar o seu número de
espiras aplicando a fórmula acima ou pela relação:
V1 = ___________________V
f= 60 Hz
B = ___________________Gauss
Smn = _________________cm2
12 Número de Espiras do Enrolamento Secundário (N2).
V  108
2
N2 =
4,44  f  B  S
[espiras]
mn
V2 → Tensão do enrolamento secundário (V);
f → Freqüência (60 Hz);
B → Indução magnética (Gauss);
Smn → Seção magnética do núcleo (cm2).
V2 = __________________V
B = ___________________Gauss
Smn = _________________cm2
Tabela de Fios de Cobre para enrolamentos
Diâmetro fio
Seção (mm2)
0,39
0,102
0,35
0,0805
0,31
0,066
0,27
0,0491
0,25
0,0415
0,22
0,0314
0,20
0,0254
0,18
0,0201
0,16
0,0154
0,14
0,0132
Diâmetro fio
Seção (mm2)
0,12
0,00951
0,112
0,00785
0,099
0,00636
0,089
0,00502
0,077
0,00385
0,068
0,00317
0,061
0,00257
0,054
0,00203
0,048
0,00158
0,044
0,00114
Esmaltado (mm)
3,32
2,06
2,65
2,6
2,11
1,88
1,68
1,5
8,35
6,65
5,27
4,15
3,3
2,63
2,09
1,65
1,34
1,3
1,2
1,04
1,07
0,96
0,86
0,77
0,69
0,61
0,55
0,48
0,44
0,818
0,65
0,515
0,407
0,322
0,255
0,204
0,159
0,126
Verificação da Possibilidade de Execução.
Apresentaremos dois métodos de verificação com os quais determinaremos se o transformador até
então calculado pode ou não ser constituído.
27.5.1 Primeiro Método.
Verifica-se inicialmente o desenho explicativo:
27.5.1.1 Cálculo da Seção da Janela (Sj).
Sj = Lj . Hj [ mm2]
Lj → Largura da janela em mm;
Hj → Altura da janela em mm.
Lj = __________________mm
Hj = __________________mm
Sj = ___________________mm2
Seção do Isolante (Si).
Si = Esp . L(isolante) [mm2]
Esp → Espessura do isolante em mm
L(isolante) → Comprimento do isolante = 2.Hj + 2.Lj [mm]
Esp = 0,5 mm
L(isolante) = ____________________mm
Si = ___________________mm2
Seção Útil da Janela (Suj).
Suj = Sj – Si
[mm2]
Sj → Seção da Janela em mm2
Si → Seção do Isolante em mm2
Sj = _________________mm2
Si = _________________mm2
Suj = _________________mm2
Seção do Cobre (SCU).
SCU = N1 . S1r + N2 . S2r [mm2]
N1 → Numero de espiras do enrolamento primário;
S1r → Seção real do enrolamento primário em mm2;
N2 → Número de espiras do enrolamento secundário;
S2r → Seção real do enrolamento secundário em mm2.
N1 = _______________espiras
S1r = ________________mm2
N2 = _______________espiras
S2r = ________________mm2
SCU = ________________mm2
Para melhor entendermos, vejamos o desenho:
Verificação Final
S
x=
Se x
S
uj
CU
 3  execução  possivel
3  execução  impossível
Suj → Seção útil da janela em mm2
SCU → Seção do Cobre em mm2
Suj = _____________________mm2
SCU = ____________________mm2
X = _____________________
Resultado:_________________________