1º - Grupos.com.br

EXERCÍCIOS DE RESISTÊNCIA DOS MATERIAIS
Entregar dia : 13/04/09
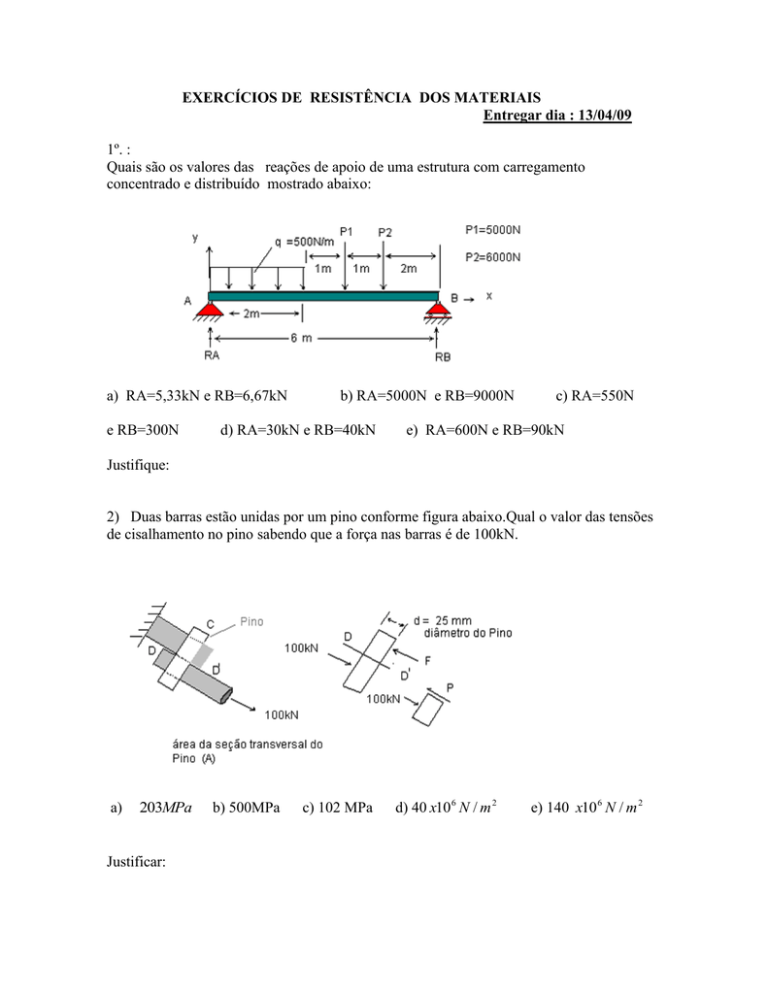
1º. :
Quais são os valores das reações de apoio de uma estrutura com carregamento
concentrado e distribuído mostrado abaixo:
a) RA=5,33kN e RB=6,67kN
e RB=300N
b) RA=5000N e RB=9000N
d) RA=30kN e RB=40kN
c) RA=550N
e) RA=600N e RB=90kN
Justifique:
2) Duas barras estão unidas por um pino conforme figura abaixo.Qual o valor das tensões
de cisalhamento no pino sabendo que a força nas barras é de 100kN.
a)
203MPa
Justificar:
b) 500MPa
c) 102 MPa
d) 40 x10 6 N / m 2
e) 140 x10 6 N / m 2
3) Qual é o valor das tensões de esmagamento(  esm. ) no furo, tensões de
cisalhamento ( parafuso) no parafuso e as tensões normais( ( normal. ) na chapa na região do
furo das juntas parafusada abaixo.
 esmagamento.na.chapa 
Dados:
P=80kN
 parafuso 
P P

A t.d
P
A
tensão de esmagamento
cisalhamento no parafuso
t=20mm
b= 75 mm
 Normal.na.chapa 
d= 25 mm
a) 400, 500 e 901 MPa
350MPa
b) 300, 162 e 450 Mpa
P
P

A b.t  t.d
tensão normal na chapa
( na região do furo)
c) 160, 163 e 80MPa d) 400, 5800 e
e) 16 , 140 e 200 MPa
Justifique:
4) Um cabo elétrico de alta tensão está sujeito a uma força de tração de 25000N conforme
a figura abaixo . Qual deve ser o diâmetro do cabo sabendo que a tensão admissível é de
100MPa.( obs.: as tensões no cabo não pode ultrapassar 100MPa).
d=?
a)
25mm
b) 44,5 mm
c) 39,3 mm
d) 5 mm
e ) 17,8 mm
Justifique.:
5) Uma barra de treliça conforme a figura abaixo ,é de madeira e está sujeita a esforço
de tração . Sabendo que a seção transversal é retangular de altura igual 300 mm, e a
tensão admissível da barra BC é de 80 MPa ; quanto mede o lado (b) da seção retangular.
A força na barra (FBC) é igual a 50kN.
Área da seção transversal= bxL
6) Determinar a força de tração numa barra de aço cilíndrica com 4 cm de diâmetro
,quando ao aplica-se força na barra ocorre uma deformação( específica) igual a
0,7 x10 3 . O módulo de elasticidade do aço é igual a 21x10 5 kgf / cm 2 .
PL
F
L
   .E...., L 
.......,..  ...........,  
Equações conhecidas :
EA
A
L
a) 10400 kgf
b) 30.000 kgf
c) 200 kgf
d) 4000 kgf
e) 18.463 kgf
Justificar.
7) Um arame com 30 m de comprimento , sujeito a uma força de tração de P=1000 kgf
alonga-se de 3cm . Determinar o módulo de elasticidade do material , sendo a área da seção
transversal do arame é igual a 0,25cm 2 .
L= 30m= 3000cm
P= 500 kgf
A= 0,25cm 2
L  3cm
PL
F
L
   .E...., L 
.......,..  ...........,  
EA
A
L
5
a) 40 x10 kgf / cm
5
2
d) 60 x10 kgf / cm
5
b) 20 x10 kgf / cm
2
6
2
e) 10x10 kgf / cm
6
c) 50 x10 kgf / cm
2
2
2
8) 4) Uma barra de aço , com seção transversal de área igual a 10.cm , está sujeita à
uma ação de forças Q=420 kgf e P 210 kgf ( veja figura abaixo ) . Calcular o alongamento
total
( L )
da barra.
L Total  2
a)
0,0035 cm
b) 0,50 cm
c) 0,0025 cm
QL1 (Q  P) L2

EA
EA
c) 2cm
d) 9 cm
e) 0,001 cm
Justificar:
9) 03- Uma barra prismática de aço de 60 cm de comprimento, é distendida(alongamento)
de 0,06 cm sob força de tração . Achar a grandeza da força sendo o volume da barra de 800
centímetros cúbicos.
a) 27.993 kgf
b)
40.000 kgf
c) 33.000 kgf
d) 45.000 kgf
e)
400 kgf
10) No ensaio de tração obtivemos de um aço SAE 1045 , a seguinte curva abaixo:
10.1)
Em 0,2% de deformação, com uma reta paralela encontramos a curva ( norma de
ensaio) em um ponto. A tensão correspondente a este ponto 1 e denominada de:
a) Tensão Máxima
b) Tensão de ruptura c) Tensão de compressão d) tensão admissível
e) Tensão de escoamento
10.2)
A tensão máxima e a tensão de ruptura são os pontos :
a) 1 e 3
b) 2 e 3
c) 1,4
d) 4 e 3
e)4e2
10.3)
Descreva como se obtém o módulo de elasticidade a partir da curva acima
.....................................................................................................................
......................................................................................................................
......................................................................................................................
10.4)
Onde encontra-se a região elástica e plástica na curva acima.
.........................................................................................................................
..........................................................................................................................
11) Qual é o momento de inércia ( Ix) da seção transversal vazada , conforme a figura
abaixo.
Ix:
bh 3
I
momento de inércia de uma seção retangular
12
Obs.: Calcule o momento de inércia do retângulo maior menos o menor.
6
a) 10x10 kgf / cm
e) 5000cm
2
4
b) 631.333cm
c) 40000kgf / cm
2
d) 210 kgf.mm
4
11) Qual é o momento de inércia ( Iy) da seção transversal vazada , conforme a figura
abaixo.
Iy:
a) 5000kgf / cm
e) 293333cm
2
4
b) 72000cm
4
12) Calcular o centróide da figura abaixo
c) 40000kgf / cm
2
d) 210 kgf.mm