Trabalho_recup_2ºbim_8ºano

COLÉGIO RESSURREIÇÃO NOSSA SENHORA
Disciplina:
Professor(a):
Matemática
Leudinésio Antonio
Data:
Tipo de avaliação:
Período:
Valor:
Trabalho
2o. Bimestre
5,0 pontos
Nota:
Nº
Aluno:
Série/Turma:
8o ano
Atenção: Responda as questões do trabalho, justificando todas as respostas.
Questão 1 (1,0 ponto)
I) Escreva as coordenadas dos pontos B, C e D sabendo que:

As coordenadas do ponto A são (- 3 , 4 )

O ponto D é simétrico ao ponto A em relação ao eixo x.___________________

A abscissa e a ordenada do ponto B são iguais a metade da ordenada do ponto D. ___________________

O ponto C tem abscissa igual a do ponto B e ordenada igual a do ponto A. _________________________
II) No esquema está apresentada parte da região central de uma cidade. Note que sua representação permite localizar cada
quarteirão por meio de uma letra e um número. O teatro, por exemplo, está localizado no quarteirão D3 .
a ) Escreva a localização do quarteirão onde está: o planetário; a biblioteca; o terminal urbano.
b ) A igreja está localizada entre quais quarteirões?
c ) Determine a localização do quarteirão em que uma pessoa mora, sabendo que ele fica três quarteirões à esquerda do
teatro.
Questão 2 (1,0 ponto)
I) Dados P = x2 + a2 – 2ax e Q = 2x2 + 5ax + 3a2, determine:
a) P + Q e seu valor numérico para a = 10 e x = – 4.
b) P – Q e seu valor numérico para a = – 0,5 e x 1,2.
II) Considere as afirmações abaixo e identifique se são verdadeiras ou falsas. Justifique sua resposta.
a) O valor numérico da expressão algébrica
a 2  ax
, quando a = 8 ; x = 10 e m = 16 é igual a
m
3.
b) Um sorvete custa x reais e um doce custa y reais. Mariana tomou 2 sorvetes e comprou 5 doces, enquanto Gabriela
tomou 3 sorvetes e comprou 2 doces. Nessas condições, a expressão algébrica que representa o valor pago por Mariana
é 3x + 2y.
c) Na multiplicação do monômio (– 6a2b) pelo monômio 2ab2, obtemos um monômio cujo valor numérico para a = 2 e b = 1
igual a – 96.
Questão 3 (1,0 ponto)
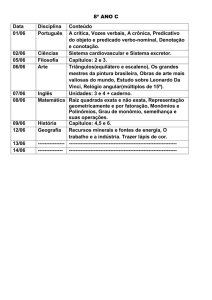
I) Observe que o quadrado ABCD é formado por dois outros quadrados e por dois retângulos.
Determine: a) O trinômio que representa a área do quadrado em destaque.
b) Considerando x = 6cm e y = 2cm, calcule a área de cada um dos quadrados e de cada um dos retângulos.
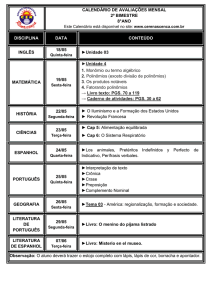
II) Observe o hexágono representado no plano cartesiano e responda às questões.
a ) Qual vértice possui o menor valor para a abscissa? E o maior valor para a ordenada?
b ) Quais devem ser as coordenadas dos vértices de um hexágono para que ele seja simétrico ao hexágono ABCDEF em
relação ao eixo x? E para que seja simétrico a ABCDEF em relação ao eixo y?
Questão 4 (1,0 ponto)
I) Efetue as operações com polinômios seguir.
a) (13x2 – 11x – 15) – (7x2 + 2x – 16)
b) (a + x).( a2 – ax + x2)
c) (a3
– 2a2 + 3) + ( a3 + a2 – 5)
d) Determine o polinômio D representa a diferença entre os polinômios: 5ax – 10x – 9a e 3ax – 8x – 12a.
e) Se você dividir (– 21a4b4) por um certo monômio, vai obter (7ab). Qual é esse monômio?
II) Determine o grau dos seguintes polinômios:
a) 3b6 – b2 + 2b ___________________
c) 2x3y – 3x5 + 4xy2 ____________
b) x + 5 ( 2 – ax2) ___________________________
d) – 5a3 – 7a2x5 + 5 __________________________
Questão 5 (1,0 ponto)
I) Sabendo que X = 2m4n3 e Y = 3m5n4, calcule:
a) X  Y
b) (X  Y)3
c)
X4  Y 3
Y
d) (2Y2 : 3X)4
II) Considerando A = 3m 4 – 2m3 + m2 – m + 1 e B = –3m4 – 3m3 – 2m2 + m – 1, podemos afirmar que os polinômios que
representam A + B e A – B são, respectivamente:
a )( ) –5m3 + m2; 6m4 + m3 – 2m – 1
b )( ) –5m3 – m2; 6m4 + m3 + 3m2 – 2m + 2
c )( ) 5m3 – m2 + 1; m4 – 5m3 + 3m2 – 2m
d )( ) 6m4 – 5m3 – m2 + 2; 6m4 + m3 – m2 – 2m + 2
e )( ) –6m4 – 5m3 – m2 – 1; 6m4 + m3 – 3m2 – 2m – 2
III) Um grupo de estudantes de meteorologia pesquisou as variações de temperatura em certa cidade.Após longa coleta de
dados, o grupo concluiu que a temperatura podia ser calculada por meio da fórmula matemática:
𝟏
𝐓 = − 𝐭² + 𝟒𝐭 + 𝟏𝟎 , na qual T representara a temperatura, e t representa a hora do dia. O grupo calculou a temperatura
𝟔
na cidade ás 12 horas e ás 18 horas. Nesse período, a temperatura diminuiu de quantos graus Celsius?