1-) Um tubo de paredes finas rola pelo chão

FAP0153 – Mecânica p/ Licenciatura – IME
Quinta Lista de Exercícios – Parte 2
06/06/2006
1-) Um tubo de paredes finas rola pelo chão. Qual é a razão entre as suas energias
cinéticas translacional e rotacional, em torno de um eixo paralelo ao seu comprimento e
que passa pelo seu centro de massa?
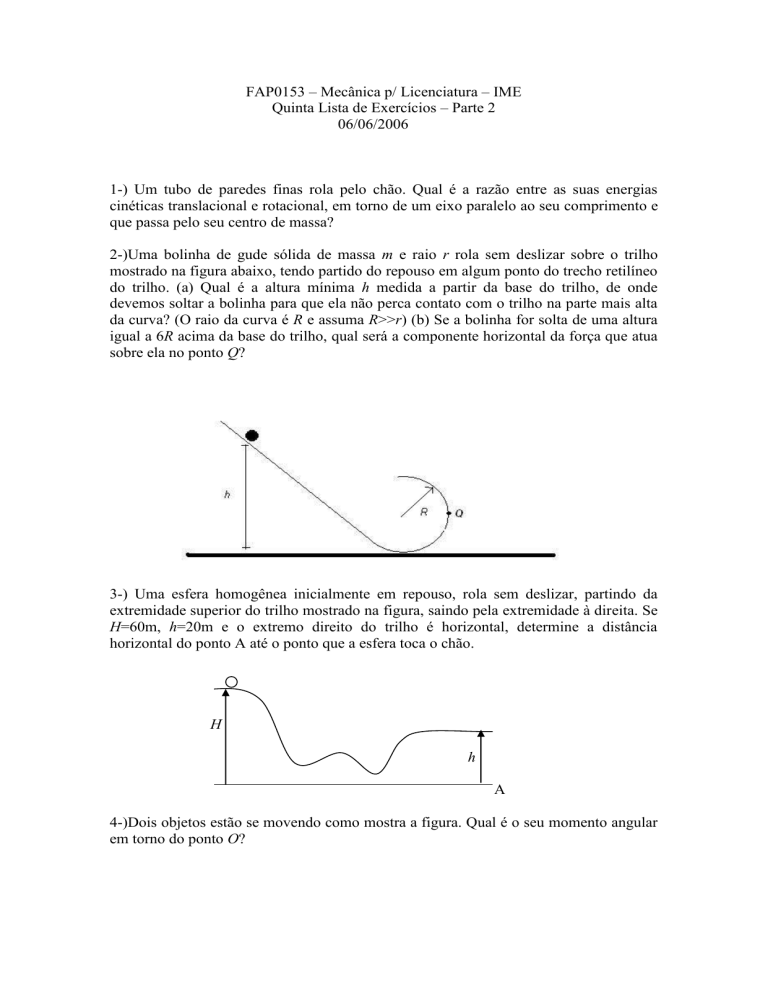
2-)Uma bolinha de gude sólida de massa m e raio r rola sem deslizar sobre o trilho
mostrado na figura abaixo, tendo partido do repouso em algum ponto do trecho retilíneo
do trilho. (a) Qual é a altura mínima h medida a partir da base do trilho, de onde
devemos soltar a bolinha para que ela não perca contato com o trilho na parte mais alta
da curva? (O raio da curva é R e assuma R>>r) (b) Se a bolinha for solta de uma altura
igual a 6R acima da base do trilho, qual será a componente horizontal da força que atua
sobre ela no ponto Q?
3-) Uma esfera homogênea inicialmente em repouso, rola sem deslizar, partindo da
extremidade superior do trilho mostrado na figura, saindo pela extremidade à direita. Se
H=60m, h=20m e o extremo direito do trilho é horizontal, determine a distância
horizontal do ponto A até o ponto que a esfera toca o chão.
H
h
A
4-)Dois objetos estão se movendo como mostra a figura. Qual é o seu momento angular
em torno do ponto O?
6,5kg
v=2,2m/s
v=3,6m/s
O
3,1kg
5-) Duas partículas, cada uma com massa m e velocidade v, movem-se em sentidos
opostos ao longo de linhas paralelas separadas por uma distância d. Encontre uma
expressão, em termos de m, v e d, para o momento angular total do sistema em torno de
uma origem qualquer
6-)Um carro de brinquedo de 3,0 kg move-se sobre o eixo x com velocidade v=-2,0t3
m/s ao longo do mesmo eixo. Para t>0, quais são (a) o momento angular do carro e (b) o
torque que atua sobre ele, ambos em relação à origem? (c) Repita (a) e (b) em relação a
um ponto (2m; 5m; 0) em vez da origem (d) Repita (a) e (b), desta vez em relação ao
ponto (2;-5;m)
7-) Um projétil de massa m é atirado do chão com velocidade inicial v0 e a um ângulo
inicial 0 acima da horizontal. (a) Encontre uma expressão para o seu momento angular
em torno do ponto de lançamento em função do tempo. (b) Determine a taxa de variação
do momento angular com o tempo. (c) Calcule r x F diretamente e compare com o
resultado de (b). Por que os resultados devem ser idênticos?
8-) Duas bolas de 2kg cada são presas às extremidades de uma barra fina de massa
desprezível de 0,50m de comprimento. A barra pode girar livremente, sem atrito, num
plano vertical, em torno de um eixo horizontal que passa pelo seu centro. Enquanto a
barra está na horizontal, uma bola de massa de vidraceiro de 50 g cai sobre uma das
bolas com velocidade de 3,0 m/s e fica grudada a ela. (a) Qual é a velocidade angular do
sistema, logo após a colisão da massa de vidraceiro? (b) Qual é a razão entre a energia
cinética do sistema inteiro após a colisão e a energia cinética da bola de massa, pouco
antes da colisão? (c) Qual será o ângulo em que o sistema irá girar até parar
temporariamente?
Massa de
Vidraceiro
Eixo de rotação
g
9-) Uma bolinha presa a um fio de massa desprezível gira em torno de um eixo com
velocidade escalar constante, mantendo-se a uma distância d de 0,5 m em relação ao
eixo; o ângulo vale 30o e o fio passa sem atrito através de um orifício O numa placa.
O fio é puxado lentamente para cima até que o ângulo passa a ser 60o. (a) Que
comprimento do fio foi puxado? (b) De que fator variou a velocidade de rotação?

d
10-) Um homem está de pé sobre uma plataforma sem atrito que gira com velocidade
angular de 1,2 rps (rotações por segundo); seus braços estão abertos e ele segura um
peso em cada mão. Nesta posição, o momento de inércia do sistema composto pelo
homem, os pesos e a plataforma é igual a 6,0 kg.m2. Se ao mover os pesos o homem
fizer o momento de inércia diminuir para 2,0 kg.m2, (a) qual será a velocidade angular
da plataforma e (b) qual será a razão entre a nova energia cinética do sistema e o seu
valor inicial? (c) O que forneceu a energia cinética adicional?
11-)Uma barata de massa m corre em sentido anti-horário na borda de um prato
giratório de raio R e momento de inércia I, que pode girar sem atrito, em relação ao eixo
que passa pelo seu centro e é perpendicular ao plano do disco. A velocidade da barata
em relação ao solo é v, enquanto que o prato gira no sentido horário a uma velocidade
angular A barata encontra um pedaço de pão na borda do prato e pára. (a) Qual é a
velocidade angular do prato depois que a barata pára?. (b) Suponha agora que a barata
esteja na condição do item (a) quando avista outro pedaço de pão num ponto distante de
r do eixo de rotação. A barata caminha lentamente, apenas na direção radial até alcançálo e pára novamente. Qual é a nova velocidade angular do sistema?
12-) Um ioiô de massa M raio interno r e raio externo R e momento de inércia ICM em
relação ao centro de massa, é puxado pelo fio enrolado em seu eixo central, de forma a
rolar sem deslizamento sobre uma mesa horizontal, através de uma força F que faz um
ângulo com a horizontal. (a) Qual a condição para o módulo de F para que o ioiô
fique em contato com a mesa? (b) Calcule a aceleração angular do ioiô (c) Mostre que
existe um ângulo crítico o o qual conforme a magnitude de , o fio se enrola ou se
desenrola, e o ioiô avança ou recua
F

13-) Prende-se ao teto uma fita métrica leve, enrolada num estojo circular de massa m e
raio r e solta-se o estojo em repouso. (a) Calcule a aceleração linear do estojo (b)
Calcule a tensão na fita (c) Calcule a velocidade linear do estojo depois que um
comprimento s da fita se desenrolou. Verifique a conservação da energia
r
m
14-) Um bloco de massa m que pode deslizar com atrito desprezível sobre um plano
inclinado de em relação à horizontal, e está ligado por um fio que passa por uma polia
de raio R e massa M, a uma massa m´ > m suspensa. O sistema é solto em repouso.
Calcule por conservação da energia, a velocidade de m´ após cair de uma altura h
M, R
m

m´