Microeconomia II - Escola Carlos Nabais

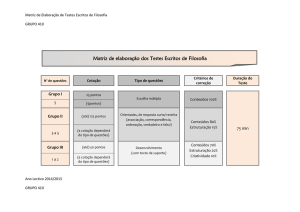
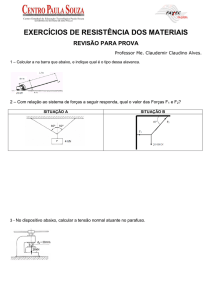
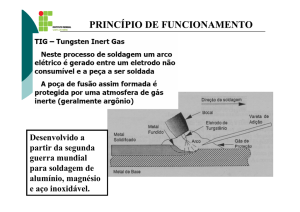
PROVA 9
Exercício 1:
Num dado país existem 100 empresas produtoras de moldes de aço (bem
X) que vendem o seu produto num mercado concorrencial. A procura é
descrita por PX  4 . Na produção de moldes estas empresas utilizam aço
(bem Y) que compram à empresa A. A função de produção de cada
empresa é dada pela expressão xi  F  yi   2 yi0.5 . Para além dos custos
com a aquisição da matéria prima, estas empresas têm ainda um custo de
transformação de 2 unidades monetárias por unidade de produto final.
A empresa A, monopolista na produção e comercialização de aço, produlo a partir de uma liga metálica que compra num mercado concorrencial e
cujo preço é dado por PZ  0.5 . Para produzir 1 unidade de aço são
necessárias 2 unidades da liga metálica.
a) Determine a expressão da função de procura de aço dirigida à empresa
A? (Cotação: 2 valores)
Resolução: A função de procura de aço dirigida à empresa A, é obtida a partir
das funções de procura de cada empresa. Estas podem obter-se da maximização
do respectivo lucro:
Max 4 2 yi0.5  pY yi  4 yi0.5
pelo que:
4
4 yi 05  pY  2 yi 0.5  0  yi  2 .
pY
Como o preço de X é totalmente determinado pela respectiva procura,
infinitamente elástica para um preço igual a 4, a procura global pode obter-se
pela mera adição das procuras individuais e é dada por:
400
y 2 .
pY


b) Qual a quantidade e o preço de equilíbrio do aço, a quantidade de
moldes produzida por cada empresa, e o lucro de cada empresa
mencionada? (Cotação: 1.5 valores)
Resolução: Para determinarmos o equilíbrio no mercado do aço temos de
resolver o problema de maximização do lucro do respectivo monopolista.
Invertendo a curva de procura obtemos pY  20 y 0.5 . Portanto, resolve-se o
problema:
Max 20 y 0.5  y ,
pelo que:
10 y 0.5  1  0  y  100 .
Portanto, as restantes variáveis assumem os valores: pY  2 , yi  1 , xi  2 ,
 X i  2 e  A  100 .
No sentido de criar uma melhor posição para a negociação do preço do
aço, as produtoras de moldes formaram uma associação empresarial.
1
c) Qual o preço que elas desejarão impor para o aço? (Cotação: 1.5
valores)
Resolução: Neste caso a associação patronal comportar-se-á como um
monopsonista. Portanto, sabendo que o custo marginal da empresa A é igual a 1,
desejará impor esse preço. Se o preço fosse superior a associação empresarial
estaria conceder lucros à empresa A; se o preço fosse inferior a empresa A não
quereria vender aço.
O Estado preocupado com o poder de monopólio da empresa A decidiu
abrir o comércio do aço ao exterior. O preço no mercado internacional é
1.5.
d) Qual o impacto dessa medida no poder negocial da associação
empresarial e da empresa A? (Cotação: 2 valores)
Resolução: Depende do poder negocial que tenham na situação anterior., em
cujas condições a empresa A e associação patronal negociarão um preço entre 1 e
2. O preço acordado poderá ser visto como uma média ponderada destes valores,
em que o peso dado a 1 é uma medida do poder negocial da associação patronal e
o peso dado a 2 é uma medida do poder negocial da empresa A. Ao abrir o
mercado ao comércio internacional o preço do aço terá de passar a ser igual a 1.5
(se fosse mais alto os compradores importariam o aço; se fosse mais baixo a
empresa A exportá-lo-ia), pelo que tudo se passará como se o poder negocial das
partes fosse de 50%, ou seja reduzir-se-ia o poder negocial da parte inicialmente
mais forte e se aumentar-se-ia o poder negocial da parte inicialmente mais fraca.
Exercício 2:
Considere uma economia constituída pelos agentes A e B. O agente A
possui uma dotação de trabalho de 400 e uma tecnologia que permite
produzir bem X de acordo com a função de produção X (l X )  l X . O
agente B possui uma dotação de trabalho de 200 e a tecnologia de
produção do bem Y dada por Y (lY )  0.1lY . Ambos têm as preferências
descritas pela função de utilidade U ( x, y )  10 ln( x)  y .
a) Considere nesta alínea que não existe mercado de trabalho, ou seja,
temos uma economia de troca pura em que o agente A tem uma dotação de
20 (isto é 400 ) unidades de X e o agente B de 20 (isto é 0.1 200 )
unidades de Y. Qual o equilíbrio competitivo desta economia? (Cotação:
2.5 valores)
Resolução: As condições de eficiência no consumo dos bens levam-nos a:
 10
x  p
 A
,

 10  p
 x B
onde p é o preço relativo do bem X. Por conseguinte, da condição de equilíbrio
no mercado do bem X resulta:
2/5
10 10
  20  p  1  x A  x B  10.
p
p
Portanto, y A  (20  10)  1  10 e yB  20  10  10 .
A partir de agora passe a considerar que existe um mercado de trabalho.
b) Determine a fronteira de possibilidades de produção desta economia e
represente-a graficamente. (Cotação: 1.5 valores)
Resolução: A fronteira de possibilidades de produção desta economia pode
obter-se a partir do seguinte sistema:
 LX  LY  600

,
 X  LX
Y  0.1L
Y

que conduz a X 2  10Y  600  Y  60 
X2
.
10
c) Determine o equilíbrio competitivo desta economia. (Cotação: 3
valores)
Resolução: Seja
px  PX / W ,
px  PY / W ,
p  p x / p y . O equilíbrio
competitivo no mercado do factor exige que:
 px 0.5(l X ) 0.5  1 l X  0.25 px 2


.
  p y  10
 p y 0.1  1


2
lY  600  0.25 p x
l X  lY  600
Utilizando agora a condição de equilíbrio no mercado do bem X:
10 10
0.5

 lX
px
px
py
py
e tendo em conta que, da optimalidade na produção do bem X, l X 0.5  0.5 px ,
resulta p x  20 . Assim, p  2 , X A  X B  10 / 2  5 , LX  0.25  400  100 ,
LY  600  100  500 , X  10, e Y  0.1  500  50. Por fim, a partir da
restrição orçamental do agente B temos PX xB  PY y B    W 200  yB  10 , e
portanto y A  40 .
d) Comente a seguinte afirmação de um dos agentes: “Estava mais
contente quando não tínhamos mercado de trabalho na economia. Isto não
me deixa acreditar nos mercados, em particular, não é possível que o
Primeiro Teorema do Bem-Estar seja verdadeiro, nem tão pouco que
tenha havido uma melhoria do bem estar social.” (Cotação: 1.5 valores)
Resolução: A afectação da alínea a) não é um óptimo para a economia da alínea
c) pois o preço relativo era de 1, mas a TMT  4 . Isto permite perceber que a
abertura do mercado de trabalho pode não induzir uma melhoria de Pareto, pelo
que é possível que de facto um dos agentes tenha ficado pior, sem que isso viole
o Primeiro Teorema do Bem-Estar. Porém, a abertura do mercado de trabalho,
induzirá então uma melhoria potencial de Pareto. É naturalmente possível que o
3/5
bem estar social tenha aumentado; isso só depende da forma como as utilidades
de cada agente afectem a função de bem-estar social.
Exercício 3:
a)
Enuncie e explique o Teorema da Impossibilidade de Arrow
(Cotação: 1.5 valores)
Resolução: O Teorema da Impossibilidade de Arrow diz que não existe nenhum
mecanismo de escolha social que satisfaça simultaneamente as seguintes
condições: as escolhas sejam completas (quaisquer duas alternativas possam ser
comparadas), reflexivas (o mecanismo de escolha social permite concluir que
uma alternativa é pelo menos tão boa quanto ela própria) e transitivas (se o
mecanismo leva à escolha de X relativamente a Y e de Y relativamente a Z,
então leva à escolha de X relativamente a Z); independentes de alternativas
irrelevantes (a escolha entre alternativas X e Y é independente das outras
alternativas existentes); compatíveis com o critério de Pareto (se todos os
elementos da comunidade preferem a alternativa X relativamente à alternativa Y,
a escolha social prefere a alternativa X à alternativa Y); e não levem à existência
de ditador (as escolhas sociais não coincidem necessariamente com as de um
elemento da comunidade).
Este Teorema tem uma grande importância para a construção de mecanismos de
escolha social, porquanto exige que os mecanismos de escolha social permitam
ditadores ou que tenham alguns elementos de irracionalidade (pelo menos uma
das outras três hipóteses não pode ser observada). Por exemplo, os mecanismos
habituais de votação não são transitivos e não respeitam a independência de
alternativas irrelevantes.
b) Suponha que num mercado de factor monopolizado (em que o
monopolista maximiza o lucro) era introduzido um preço máximo. Que
impacto teria isso sobre o preço e a quantidade de equilíbrio do factor.
Explique através de uma análise gráfica. (Cotação: 1.5 valores)
Resolução: A existência de um preço máximo limita a procura de factor: ainda
que o valor da produtividade marginal seja muito elevado, o preço não pode
exceder o máximo, pelo que não há procura de factor acima do preço máximo.
Portanto, a procura passa a ter um segmento horizontal ao nível do preço
máximo e até que a quantidade total procurada coincida com aquela para a qual o
valor da produtividade marginal do factor seja igual ao valor máximo do preço.
Recorrendo à figura seguinte podemos facilmente compreender os possíveis
efeitos da imposição do preço máximo:
S3
S2
S1
Caso a procura intersecte a receita marginal como S1 , a imposição do preço
máximo não tem qualquer efeito. Na situação ilustrada por S2 , o preço de
4/5
equilíbrio diminui e a quantidade transaccionada aumenta. Na situação ilustrada
em S3 , é possível que o preço e a quantidade diminuam.
c) Considere uma economia de troca pura com dois agentes e dois bens.
As preferências dos agentes são homotéticas (isto é, as TMS’s apenas
dependem dos rácios em que se consomem os bens) e os bens são
substitutos imperfeitos. Identifique o conjunto de afectações justas.
(Cotação: 1.5 valores)
Resolução: Sendo as preferências homotéticas, a curva de contrato pode ser a
diagonal da caixa ou passar sempre acima ou abaixo da diagonal da caixa
(análogo ao que se passa na caixa dos factores se ambas a funções de produção
forem CRS).
Se a curva de contrato for a diagonal da caixa, a única afectação justa é o centro
da caixa. Com efeito a afectação do centro da caixa é eficiente (por ela passa a
curva de contrato) e satisfaz o critério da ausência de inveja (os agentes têm
cabazes iguais). Uma outra afectação da diagonal da caixa será eficiente mas não
satisfará o critério da ausência de inveja (um agente tem mais de ambos os bens
do que o outro, pelo que o segundo inveja o cabaz do primeiro).
Caso contrário, suponhamos que a curva de contrato passa sempre acima da
diagonal da caixa. Sabemos que a afectação correspondente ao equilíbrio
competitivo que parta de uma dotação inicial igualitária é justa. As restantes
afectações justas correspondem a uma parte contínua da curva de contrato, que
inclui aquela afectação e que podemos identificar com o auxílio do seguinte
gráfico, onde temos representada a curva de contrato e duas curvas de
B
indiferença (uma para cada agente).
a
b
b
’
A
a
’
As afectações a e b estão sobre a curva do contrato, e ao compará-las com as
afectações resultantes da troca de cabazes entre os agentes (respectivamente a’ e
b’) concluimos que satisfazem a ausência de inveja, pelo que são justas. Por
construção, em qualquer afectação sobre a curva de contrato abaixo de b o agente
A invejará o agente B, pelo que não pode ser justa. De modo análogo, em
qualquer afectação sobre a curva de contrato acima de a o agente B invejará o
agente A, pelo que não pode ser justa. Por fim, qualquer afectação sobre a curva
de comtrato entre a e b necessariamente satisfará a ausência de inveja. Portanto,
as afectações justas correspondem ao segmento da curva de contrato entre a e b.
5/5