Física II – Computação

Eletromagnetismo – C. F. Biomoleculares – FFI 0752
PROVA SUBSTITUTIVA
(Individual e Sem Consulta)
Obs: Caso necessário, utilize o formulário no verso da prova.
Prof. Paulo Miranda
Data: 08/07/11
1) (2,5 pontos) O plasma é um gás ionizado, contendo elétrons livres e íons positivos, mas cuja carga
total líquida é nula (gás neutro). Nesse gás, há uma frequência característica, denominada
frequência de plasma, acima da qual as ondas eletromagnéticas são pouco atenuadas, e o gás
condutor torna-se transparente. (a) Por que podemos desprezar a contribuição dos íons positivos ao
calcular a frequência de plasma do gás? (b) Calcule o comprimento de onda na frequência de
plasma para a ionosfera, onde a densidade típica de elétrons livres é 1012 m-3. A qual região do
espectro eletromagnético corresponde esse comprimento de onda? Dica: use a expressão para a
dispersão do índice de refração obtida em classe (veja formulário) e faça as aproximações
adequadas.
2) (2,0 pontos) (a) Considere um elétron de massa m e carga –e sendo acelerado a partir do repouso
em um campo elétrico uniforme, até que atinja a energia cinética U após percorrer uma distância d.
Calcule a potência emitida pelo elétron sob a forma de radiação eletromagnética durante sua
aceleração. (b) Considere agora que o elétron realiza um movimento circular uniforme de raio R,
com a mesma energia cinética U (por exemplo, se estiver em uma região com campo magnético
uniforme). Calcule a potência emitida sob a forma de radiação eletromagnética durante o
movimento. (c) Se d  R, em qual situação acima a potência emitida é maior? OBS: Admita em
ambos os casos que a potência emitida é pequena, de modo que ela não altera apreciavelmente o
movimento do elétron, que não é relativístico (v << c).
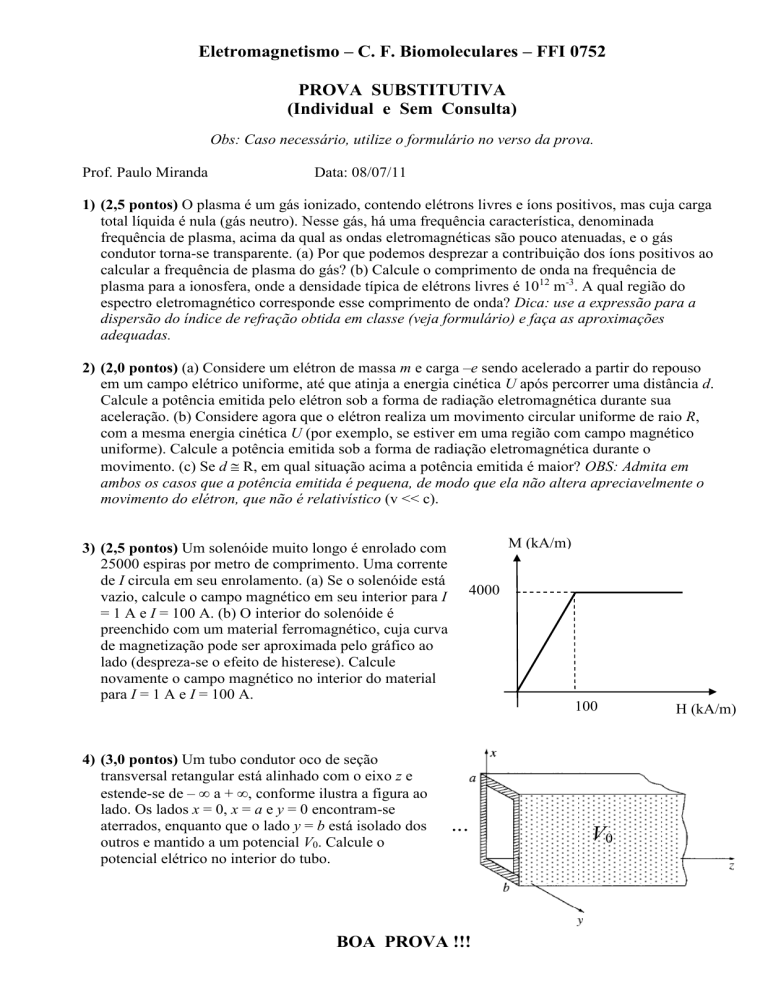
3) (2,5 pontos) Um solenóide muito longo é enrolado com
25000 espiras por metro de comprimento. Uma corrente
de I circula em seu enrolamento. (a) Se o solenóide está
vazio, calcule o campo magnético em seu interior para I
= 1 A e I = 100 A. (b) O interior do solenóide é
preenchido com um material ferromagnético, cuja curva
de magnetização pode ser aproximada pelo gráfico ao
lado (despreza-se o efeito de histerese). Calcule
novamente o campo magnético no interior do material
para I = 1 A e I = 100 A.
4) (3,0 pontos) Um tubo condutor oco de seção
transversal retangular está alinhado com o eixo z e
estende-se de –  a + , conforme ilustra a figura ao
lado. Os lados x = 0, x = a e y = 0 encontram-se
aterrados, enquanto que o lado y = b está isolado dos
outros e mantido a um potencial V0. Calcule o
potencial elétrico no interior do tubo.
M (kA/m)
4000
100
...
BOA PROVA !!!
V0
H (kA/m)
Dados:
o = 8,8510-12 F/m
m = 9,1110-31 kg
o = 410-7 Tm/A
e = 1,610-19 C
c = 2,998108 m/s
Formulário:
bg
n2   1 

 sen  mx  sen  nx  dx 
0
Coordenadas esféricas:
Coordenadas cilíndricas:

2
Ne 2
m o
 nm

j
fj
2
j
  2  i j


 cos  mx  cos  nx  dx  2 
0
nm