fis22005

Física – 2
Valores de algumas grandezas físicas
Aceleração da gravidade: 10 m/s2
Densidade da água: 1 g/cm3
Carga do elétron: 1,6 x 10-19 C
Constante de Planck: 6,6 x 10-34 J.s
Velocidade da luz no vácuo: 3 x 108 m/s
Índice de refração do ar: n = 1,0
sen 30 = 0,5
sen 45 = 0,7
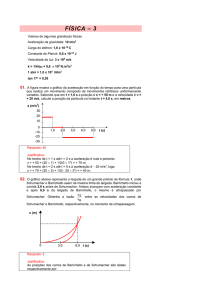
01. A figura mostra um gráfico da velocidade em função do tempo de um veículo
que realiza um movimento composto de movimentos retilíneos uniformes.
Calcule a velocidade média do veículo no intervalo de t = 0 até t = 5 h, em
km/h.
v (km/h)
30
20
10
0
-10
-20
-30
1
2
3
4
5
t(h)
Resposta: 2
Justificativa:
Sabemos que: x = (30  1) + (0  1) + ( 20  1) + (0  2) = + 10 km.
Logo: vmédia = x / t = 10/5 = + 2 km/h.
02. No instante t = 0 um menino lança uma pedra para cima. Após 1,0 s, o
movimento da pedra ainda é ascendente com uma velocidade que é a metade
da velocidade inicial de lançamento. Supondo que o atrito com o ar pode ser
desprezado, calcule a altura máxima atingida pela pedra, em metros.
Resposta: 20
Justificativa:
Usando a equação para velocidade tem-se que:
v = v0  gt ou v0/2= v0  (10  1)  v0 = + 20 m/s.
Usando a equação de Torricelli tem-se que:
v2 = v02  2g(y) ou 02 = 202  2  10 (y)  (y) = + 20 m.
03. O gráfico abaixo representa a largada de um grande prêmio de fórmula 1, onde
Schumacher e Barrichello saem da mesma linha de largada. Barrichello iniciou a
corrida 3,0 s antes de Schumacher. Ambos avançam com aceleração constante
e após 6,0 s da largada de Barrichello, o mesmo é ultrapassado por
aS
Schumacher. Determine a razão
entre as acelerações dos carros de
aB
Schumacher e Barrichello, respectivamente, no momento da ultrapassagem.
x (m)
0
3
6
t (s)
Resposta: 4
Justificativa:
As posições dos carros de Barrichello e de Schumacher são dadas
respectivamente por:
1

xB ( t )  aBt 2

2
  xB t  6   xS t  6   36aB  9aS  aS  4aB
1
xS ( t )  aS t  3 2 

2
aS
4
aB
04. Deseja-se descer uma geladeira de 100 kg do terceiro andar para o térreo de
um edifício, mas a corda disponível suporta no máximo 90 kg. Calcule a
aceleração mínima, em m/s2, que a geladeira deve ter de modo a não
ultrapassar o limite de peso da corda. Considere desprezível o atrito com o ar.
Resposta: 1
Justificativa:

T

a

P
P = peso da geladeira
T = tração máxima suportada pela corda = 900 N
a = aceleração de descida da geladeira
P  T  ma
mg  T  ma
900
a  g
 10  9  1,0 m / s2
100
05. Dois automóveis de 1000 kg chocam-se frontalmente quando suas velocidades
são iguais a 90 km/h. O choque dura 10 ms e os dois automóveis ficam em
repouso imediatamente após este intervalo. Obtenha o módulo da força média
que cada automóvel exerce sobre o outro durante a colisão, em unidades de 105
N.
Resposta: 25
Justificativa:
A força média exercida sobre um dos carros devido à colisão é dada
por:
F
variação do momento
intervalo de tempo
F
p m  v 10 3  25


 25  10 5 N
t
t
10  10  3
06. Um bloco é lançado no ponto A do trajeto mostrado na figura. A velocidade do
bloco no ponto A é v0 = 17 m/s. Sabendo que quando o bloco passa pelo ponto
B a velocidade é v0/2, calcule a velocidade do bloco no ponto C, em m/s.
Despreze os efeitos do atrito do bloco com a superfície e o ar.
v0
B
a
A
4a
C
Resposta: 34
Justificativa:
Conservação da energia mecânica.
EA = ½(mv02) = EB = ½(m(v0/2)2) + mga = EC = ½(mvc2)  mg(4a)
Logo, mga = ¾(½ (mv02)) e portanto ¼(½ (mv02)) = ½ (mvc2)  5mga
vc = 2v0 = 34 m/s.
07. Duas caixas d’água cilíndricas idênticas possuem 3,0 m de altura e área da
base 2,0 m2. As duas caixas contêm água até a metade e estão interligadas
como mostra a figura. Determine o trabalho realizado pela bomba B, em
unidades de 103 J, para esvaziar uma caixa e encher a outra completamente.
Despreze o volume de água contido nos dutos de conexão e os efeitos de atrito
da água.
Resposta: 45
Justificativa:
O trabalho realizado pela bomba B é igual à diferença de energia
gravitacional antes e depois de esvaziar uma das caixas.
W  mgh
Onde h é igual à meia altura das caixas d' água e m é a massade água
de uma das caixas
W  a  V   10  1,5
W  103  3  15  45  103 J
08. O gráfico abaixo mostra as quantidades de calor absorvidas por dois objetos, A
e B, de massas mA = 5,0 g e mB = 37 g, em função de suas temperaturas.
Obtenha a razão, cA/cB, entre os calores específicos dos corpos A e B.
Calor (J)
200
A
150
100
B
50
0
0
20
40
60
80
100
o
Temperatura ( C)
Resposta: 74
Justificativa:
Q A  m A c A TA 

QB  mBc B TB 
Q A 100


 mAc A 
TA
10
mAc A

 10

QB 50
mBc B

 mBc B 

TB
50
c A 370

 74
cB
5
09. Uma certa quantidade de gás ideal contida em um sistema, constituído de um
cilindro com êmbolo sem atrito, sofre uma transformação termodinâmica
ABCDA, indicada no diagrama da figura. O sistema está isolado termicamente
da vizinhança, exceto a base do cilindro que está em contato com uma fonte
térmica com a qual pode trocar calor durante o processo. Calcule a quantidade
de calor trocada durante a transformação, em unidades de atm  L.
p (atm)
C
D
B
A
5,0
4,0
3,0
2,0
1,0
0
0
1,0
2,0
3,0
4,0
5,0 V (L)
Resposta: 12
Justificativa:
AB = 2  (1  5) =  8 atm.L; BC = 0; CD = 5  (5  1) = + 20 atm.L;
DA = 0; total = +12 atm.L
1ª Lei da termodinâmica: E = Q –  = 0 = Q – total  Q = 12 atm.L.
10. A figura abaixo mostra três fotografias consecutivas e superpostas de uma
onda transversal viajante numa corda. O intervalo entre duas fotografias
consecutivas é de 0,05 s e é menor do que o período da onda. A partir da
figura, determine a velocidade da onda em m/s.
y (mm)
t=0,0 s
t=0,05 s
t=0,10 s
1,0
0,5
0,0
-0,5
-1,0
0
0
1,0
2,0
3,0
x (m)
Resposta: 10
Justificativa:
Em 0,05 s a onda deslocou-se 0,50 m. Portanto a velocidade é:
0,50
 10 m / s
0,05
11. Um feixe de luz incide num prisma imerso no ar, conforme indica a figura
abaixo. Após sofrer reflexão parcial na face AC, um feixe de menor intensidade
emerge através da face AB. Determine o valor do ângulo , em graus, se o
índice de refração do prisma é 1,4 para o comprimento de onda do feixe de luz
incidente.

A
B
60
30
C
Resposta: 45
Justificativa:
Usando a lei de Snell na face de saída do
raio luminoso, temos:
n sen30  sen , portanto:
  arcsen(1,4  0,5)  arcsen(0,7)
Concluímos que   45 

A
B
o
30
12. Duas cargas puntiformes, q1 = +1 C e q2 = 4 C, estão fixas no vácuo a uma
distância de 1,0 m entre si. Uma terceira carga puntiforme e positiva q3 é
posicionada ao longo da linha reta que passa pelas outras duas. Calcule a
distância, em metros, entre a terceira carga e a carga positiva de forma que ela
permaneça em equilíbrio estático.
Resposta: 1
Justificativa:
Para que haja equilíbrio, a carga q3, por ser positiva, não pode ficar entre as
cargas q1 e q2 e, por outro lado, deve ficar mais próximo da carga q1 do que da
carga q2.
Então,
1
|F13| = |F23|  kq1q3/x2 = k|q2|q3/(x + 1)2  3x2  2x  1 = 0  x = 
 1 / 3
x=1m
13. No circuito elétrico esquematizado abaixo, os valores das resistências estão
dadas em ohms. Calcule a resistência equivalente entre os pontos A e B , em
ohms.
10
10
5
5
10
10
A
B
Resposta: 5
Justificativa:
O problema é resolvido acompanhando-se a seqüência de figuras
abaixo.
10
10
5
5
5
A
B
10
10
5
10
A
B
10
5
5
A
B
10
10
A
B
5
A
B
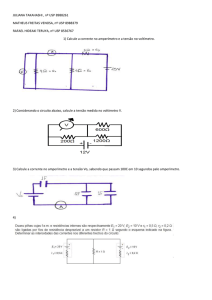
14. Um amperímetro com resistência interna de 10  é projetado para medir uma
corrente máxima de 1,0 A. Adicionando-se um resistor de 1,0  em paralelo,
como indicado na figura, é possível usar o amperímetro para medir correntes
maiores. Quando ligado em um circuito externo entre os pontos A e B, o
amperímetro indica 1,0 A. Calcule a corrente I no circuito, em amperes.
Amperímetro
10 
I
A
B
1,0 
Resposta: 11
Justificativa:
Quando estiver passando 1,0 A no amperímetro, teremos VAB =10 x
1,0 = 10 V, portanto a corrente no resistor de 1,0  será:
V
10
i  AB 
 10 A . Logo a corrente no circuito será I = 1 + 10 = 11
1,0
1,0
A
15. A figura mostra um seguimento de um condutor na forma de um L de
comprimento 7,0 cm, por onde circula uma corrente elétrica de 100 A. O
condutor em L está numa região do espaço onde existe um campo magnético
de módulo 5,0 T, perpendicular à página e entrando na mesma (ver figura).
Calcule o módulo da força magnética resultante, que atua no condutor, em
newtons.
4,0 cm
i
y
3,0 cm
x
i
Resposta: 25
Justificativa:
 


A força resultante é: F  Fy  Fx , onde Fy é a força sobre o

seguimento paralelo ao eixo x e Fx é a força sobre o seguimento
paralelo ao eixo y.
Fy = ILxB = 100  0,04  5 = 20 N; Fx = ILyB = 100  0,03  5 = 15 N
F  20 2  15 2  25 N.
16. Um átomo de hidrogênio no estado excitado correspondente ao nível n = 3,
decai para o estado fundamental (n = 1), podendo emitir radiação em três
comprimentos de onda diferentes. Determine o menor comprimento de onda
que será emitido, em unidades de 10-8 m.
n=4
n=3
-0,85 eV
n=2
-3,4 eV
n=1
-13,6 eV
-1,51 eV
Resposta: 10
Justificativa:
O menor comprimento de onda equivale à máxima energia. Logo,
c
hf  h  (E3  E1)  1,51  ( 13,6) =12


6,6  1034  3  108
19
12  1,6  10
 10,3  108 m