Estudo do Sinal de uma Função do 2° Grau

29 - Estudo do Sinal de uma Função do 2° Grau
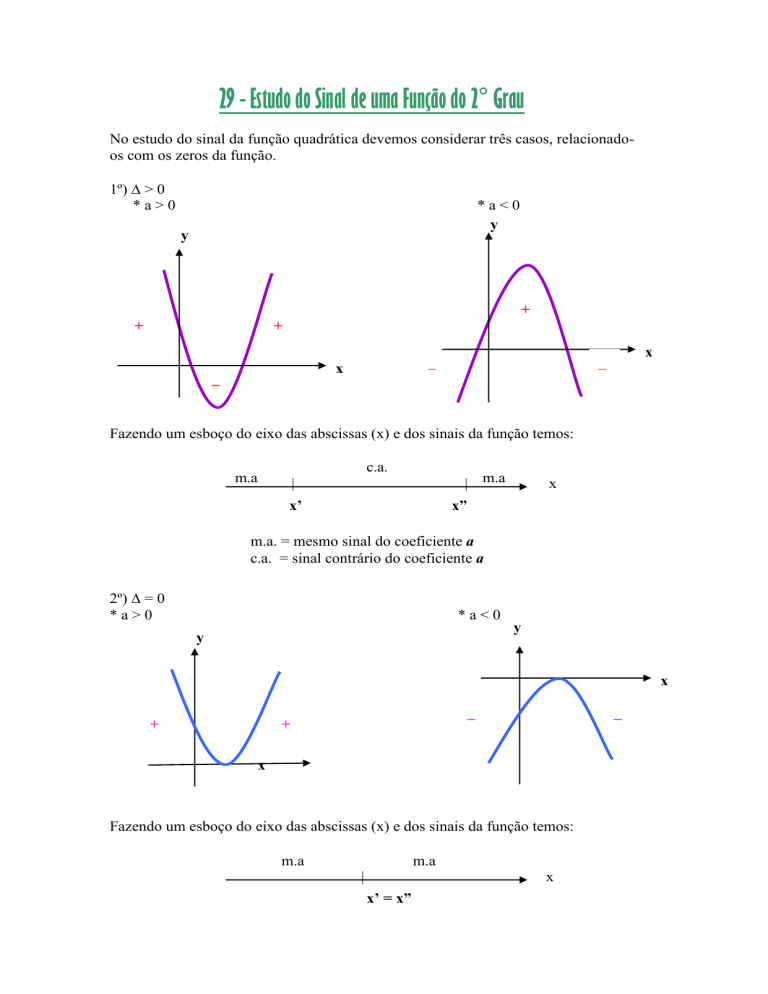
No estudo do sinal da função quadrática devemos considerar três casos, relacionadoos com os zeros da função.
1º)  > 0
*a>0
*a<0
y
y
+
+
+
_
x
_
x
_
Fazendo um esboço do eixo das abscissas (x) e dos sinais da função temos:
m.a
c.a.

 m.a
x’
x
x”
m.a. = mesmo sinal do coeficiente a
c.a. = sinal contrário do coeficiente a
2º)  = 0
*a>0
*a<0
y
y
x
+
_
+
_
x
Fazendo um esboço do eixo das abscissas (x) e dos sinais da função temos:
m.a
m.a

x
x’ = x”
3°)  < 0
*a>0
*a<0
y
y
x
+
+
+
_
_
_
x
Fazendo um esboço do eixo das abscissas (x) e dos sinais da função temos:
m.a
x
Assim estudar o sinal de uma função quadrática é dizer para que valores de x
temos:
f (x) > 0
f (x) < 0
f (x) = 0
Não esqueça f (x) = y
Exemplos:
1) Estude o sinal das seguintes funções:
a)f (x) = x² - 6x + 5
b)f (x) = - x² + 2x – 1
c) f (x) = x² – 2x + 4
2) Para que valores de m se tem a função f (x) = x² + 4x + (m – 5) positiva para
qualquer valor real de x?
3) Para quais valores de k a função f (x) = -2x² + 6x + (k – 1) assume valores não
positivos?
Aula preparada pela professora
Jane Précaro