Unidade 4 TP01

Unidade 4 TP01
p. 175
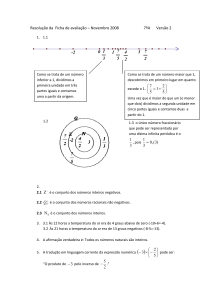
Um gráfico de blocos tridimensional
Os impostos têm subido, os preços têm subido, mas os salários estão estáveis ou, para
muitos que não têm trabalho fixo, estão decrescendo. A ilustração a seguir, um gráfico inovador e
criativo, mostra de quanto variaram, em porcentagem, os salários médios dos trabalhadores
brasileiros, de 1994 a 2001.
Podemos ver que, em 1994, houve um aumento percentual de 6% nesse salário médio; e esse
aumento foi ainda maior em 1995: 11%; o aumento não foi tão grande em 1996, mas ainda foi
significativo:7%; já em 1997 houve um aumento de apenas 2%. Em 1998 o salário médio
permaneceu estável, sua variação foi de 0%. Em 1999, porém, houve uma queda no rendimento
médio, em 5,5 por cento. Isso é indicado, no gráfico, por uma variação negativa, em um bloco
abaixo da reta horizontal. Após essa queda em 1999, o salário médio continuou baixando, mas a
variação foi pequena, em 2000: 0,6%. Em 2001 continua a haver diminuição do salário médio dos
trabalhadores brasileiros, dessa vez em 3,9%.
Atividade 6 p. 176
a) Considerando em conjunto os anos de 1994 a 1998, qual foi a variação total do salário
médio dos trabalhadores brasileiros, em porcentagem?
b) Considerando os anos de 1999 a 2001, qual foi a variação total do salário médio dos trabalhadores
brasileiros, em porcentagem?
c) Considere separadamente as variações dos itens a) e b) e diga se cada uma foi de aumento
ou de diminuição.
p. 177
Vamos voltar a pensar sobre a atividade 6. Provavelmente, no item b) você somou os valores
5,5 , 0,6 e 3,9. No item c), você deve ter respondido que essa variação foi de diminuição. Ou seja,
para somar valores negativos, você somou como se fossem positivos e a interpretação dada foi
equivalente a atribuir sinal negativo ao resultado. É o que estamos chamando de aquisição de
conhecimento em ação.
Um recado para a sala de aula
Compare a forma como foi introduzida a soma de números inteiros, vinculada a uma
situação do contexto social que induziu uma ação operatória natural. É um exemplo, portanto, do
que chamamos conhecimento em ação. É bem diferente do que fazem muitos livros didáticos, que
começam dando uma regra, em termos bem matemáticos, do tipo:
“Para somar números negativos somamos seus valores absolutos e atribuímos sinal negativo ao
resultado”.
Na maioria das vezes, nem explicam as razões da regra, e fazem que os alunos as apliquem em
exercícios matemáticos, sem contextualização que as torne mais claras. Desse modo, o
conhecimento matemático fica impositivo, sem compreensão e sem significado, e o aluno deve
incorporá-lo ao acervo da memória, para poder usá-lo em outra ocasião. Do modo como propomos,
o aluno constrói naturalmente os procedimentos e atribui significado ao que faz. Em outra situação,
não terá problema em proceder de modo análogo.
Atividade 8
a) Consulte um livro didático de 6a série e verifique como ele introduz a soma de números
negativos. Cite título, autor, editora e ano de publicação. Transcreva o trecho
correspondente, e analise se a proposta do autor é semelhante ou não à que apresentamos,
mostrando semelhanças e diferenças.
b) Para você, qual proposta é mais eficaz para a aprendizagem? Por quê?
p. 178
A multiplicação de dois números negativos
É provável que você já se tenha questionado sobre a razão de outras regras de sinais nas
operações com os números negativos. Por exemplo, sobre o fato de o produto de dois números
negativos dar um número positivo.
Atividade 9
a) Você já encontrou em algum livro didático uma explicação lógica para essa regra? Caso
tenha encontrado, copie a explicação, citando o título, o autor, a editora e o ano de
publicação.
b) Você considera que a explicação encontrada é clara para os alunos?
c) Você tem outro modo de explicar esse fato aos seus alunos? Se não tem, pense em um,
usando a sua criatividade e os seus conhecimentos matemáticos.
p. 179
Procurando um significado para a multiplicação de dois números negativos
Talvez um bom início para resolver essa questão seja refletir sobre a interpretação da
multiplicação de dois números negativos.
Lembremos que em uma multiplicação, mesmo entre números positivos, os dois números a
serem multiplicados não têm significados iguais, como ocorre com as parcelas de uma soma.
Na multiplicação de dois números naturais, o primeiro fator indica quantas vezes o segundo
deve ser adicionado. O resultado da adição é o produto dos dois.
A mesma interpretação aplica-se quando o primeiro fator é um número natural e o segundo,
um número negativo:
3 x (-2) pode ser visto como o resultado da adição de três parcelas iguais a (-2), isto é:
(-2) + (-2) + (-2), igual a -6.
Entretanto, que interpretação dar quando o primeiro fator é negativo? Por analogia e
coerência matemática, podemos dizer que ele indica quantas vezes o segundo deve ser subtraído, ou
retirado.
Uma abordagem financeira
Agora pense um pouco: se valores negativos são retirados ou desaparecem (por exemplo, no
caso de dívidas serem perdoadas) então sua situação financeira melhora, certo? Veja um exemplo
simulado:
Saldos e parcelas a receber: 205,00 + 55,00 + 20,00 = 280,00
Dívidas: 40,00 + 60,00 + 60,00 + 60,00 + 60,00 = 280,00
No fundo, você está zerado. Tudo que você tem ou receberá já está comprometido. Veja a
tabela:
Créditos
Débitos
Saldo
205,00
55,00
20,00
Totais
280,00
40,00
60,00
60,00
60,00
60,00
280,00
0,00
Entretanto, suponha que uma liminar da Justiça impediu a prefeitura de cobrar-lhe as quatro
parcelas de 60,00. Como fica sua situação agora?
p. 180 e 181
Créditos
Totais
Débitos
205,00
55,00
20,00
40,00
280,00
40,00
Saldo
240,00
Será coincidência? Você estava sem nada e agora tem R$240,00 para gastar, exatamente o
valor de 4 parcelas de R$60,00. Será que retirar quatro dívidas de R$60,00 corresponde a somar
R$240,00? Ou seja: Será que (-4) x (-60,00) = 240,00?
Uma abordagem matemática
Ao ampliar o conjunto dos números naturais para o conjunto dos números inteiros, os
matemáticos procuravam definir as novas operações (positivos com negativos e negativos com
negativos) de modo coerente com as operações que já existiam e conservando as propriedades que
valiam para essas operações com números naturais. Desse modo, foram descobrindo como definir
as operações entre os números inteiros, pela exigência da validade de certas propriedades, como a
distributividade e a comutatividade.
Lembrete
Propriedade distributiva: para três números naturais quaisquer a, b e c vale ax(b+c) = axb + axc
Propriedade comutativa da multiplicação: para dois números naturais quaisquer a e b vale
axb = bxa
Essas propriedades eram tão úteis para os cálculos que os matemáticos quiseram mantê-las
para os números inteiros, racionais e reais.
1) Mantendo para os números inteiros a propriedade distributiva da multiplicação em relação à
adição os matemáticos sabiam que deviam ter:
3 x [4 + (-4)] = 3 x 0 = 0
(A)
Por outro lado, impondo a distributividade, obtinham:
3 x [4 + (-4)] = 3 x 4 + 3 x (-4) = 12 + 3 x (-4) (B)
De (A) e (B) concluíam que 12 + 3 x (-4) = 0, ou seja, que a soma de 12 com 3 x (-4) dá
zero.
Então pensavam: qual o número que somado a 12 dá 0? Só pode ser: –12.
Concluíam que 3x (-4) = -12.
Isso confirmava uma outra idéia dos matemáticos, a de que deviam ter:
3 x (-4) = (-4) + (-4) + (-4) = -12.
Desse modo, para a e b números naturais, sabiam que a x -b = -(a x b).
2) Mantendo para os números inteiros a propriedade comutativa da multiplicação
Do mesmo modo, impondo que a multiplicação nos inteiros fosse comutativa, obtinham:
–b x a = a x -b = -(b x a).
Faltava ainda saber quanto deveria valer o produto de dois inteiros negativos. Veja como
fizeram isso, impondo novamente a distributividade:
Partindo de um exemplo numérico: - 4 x (-3+3) = -4 x 0 = 0 e impondo que valesse a
distributividade:
0 = (-4) x (-3 + 3) = (-4) x (-3) + (-4) x 3 = (-4) x (-3) + (-12)
Como o único número que somado a –12 e dá 0 é 12, concluíam que (-4) x (-3) devia valer
12.
Na seção 3 você poderá ver outros modos de evidenciar, para os alunos, que o produto de dois
números negativos dá um número positivo.
Interpretando o sinal de outros produtos – Sintetizando o que fizemos
Pela abordagem matemática, foi possível chegar ao sinal do produto (-3)x(-4). Para isso, inferimos
antes o resultado do produto 3x(-4) e de (-4) x 3 (usando a comutatividade).
A abordagem financeira interpretou o resultado de (-3)x(-4) diretamente, sem passar pelos
outros produtos. Contudo, seria possível dar também a eles uma interpretação financeira. Por
exemplo:
3 x (-4) pode ser visto descrevendo a existência de 3 dívidas de 4 cada uma, o que
corresponderia a uma dívida total de 12, descrita por -12. Ou seja: 3 x (-4)= -12.
Já (-4) x3 pode ser visto como a retirada de 4 parcelas positivas de 3 (créditos), o que
corresponde à retirada de 12 no total, equivalente, portanto, a um débito de 12. Ou seja:
(-4) x3 = -12.
Nesta seção, os conteúdos de Matemática trabalhados foram:
Gráficos não cartesianos:
- Gráficos de colunas (planos) ou de blocos (tridimensionais).
- Gráficos circulares e sua construção (proporções, medidas de ângulos, uso do transferidor).
- Vantagens e desvantagens do gráfico de colunas e do gráfico circular.
Números inteiros:
- a lógica dos sinais atribuídos aos resultados de operações com números inteiros (sob os pontos de
vista matemático e financeiro).
p. 185
Uma abordagem por observação de padrões
Observe a tabela:
Multiplicar por 2
3
2
1
0
Resultados
6
4
2
0
-1
-2
A tabela nos diz que 3 x 2 = 6; 2 x 2 = 4; 1 x 2 = 2; 0 x 2 = 0.
Observando os números da segunda linha, você percebe que eles seguem um padrão. Que
padrão é esse? Seguindo-o, você pode imaginar qual será o próximo número dessa linha, mesmo
sem olhar para os valores da primeira. O próximo número deve ser -2, porque os números da
segunda linha diminuem de 2 unidades cada vez que mudam de coluna, e 0 - 2 = - 2. Do mesmo
modo, você conclui que o último número deve ser - 4. Isso lhe permite escrever:
(-1) x 2 = -2 e
(-2) x 2 = -4.
Outras tabelas permitem inferir os resultados de outras multiplicações. Veja as sugestões
apresentadas nos PCN de 5a a 8a séries, no capítulo Orientações didáticas para terceiro e quarto
ciclos, na parte chamada Números Inteiros.
p. 186
Uma abordagem por processos de cálculo não convencionais
Vamos tentar fazer a operação:
0 - 2 x (-3) ou, de 0, tirar 2 vezes –3:
0
- 2 x ( -3)
Como podemos fazer isso, se não dispomos de nenhum -3 para ser retirado? Podemos usar um
artifício, escrevendo 0 (zero) de outra maneira:
0+3-3+3-3
- 2 x -3
Retirando duas vezes a quantidade -3, sobram →
0+3+3=6
Portanto, 0 - 2 x -3 = - 2 x -3 = 6.
Cálculos como esses nos permitem obter naturalmente muitos resultados envolvendo
operações com números negativos, sem uso de regra alguma.
Aprendendo sobre Educação Matemática - Aplicando a Teoria dos Quadros
Você reparou que as operações entre números inteiros foram trabalhadas e explicadas em diferentes
representações (ou quadros, como você aprendeu na Unidade 2 do TP1): financeira, matemática,
por observação de padrões e por cálculos alternativos? Trata-se de um exemplo concreto de como
explorar um conceito em diferentes quadros. Como já salientamos, isso aumenta o entendimento
conceitual dos alunos e atende às diferenças de cognição e de compreensão entre eles, pois cada
aluno compreende melhor um conceito sob certa abordagem.