2a Lista de Materiais Elétricos – prof. Barbieri 6o Sem. 1) Responda

2a Lista de Materiais Elétricos – prof. Barbieri 6o Sem.
1) Responda:
a) O que é um material isolante ou dielétrico?
materiais isolantes são substâncias em que os elétrons e íons não podem se
mover em distâncias macroscópicas como os condutores devido a presença de
poucos elétrons livres e que resistem ao fluxo dos mesmos (alta resistência
elétrica).
Dielétrico: é o meio no qual é possível produzir e manter (armazenar) um
campo elétrico com pequeno ou nenhum suprimento de energia de fontes
externas.
b) Explique o processo de polarização em materiais dielétricos e mostre quais são
os dois tipos de polarização
Uma propriedade fundamental dos materiais dielétricos é a polarização de suas
partículas elementares, quando sujeitas à ação de um campo elétrico.
Devido a essa polarização, os materiais dielétricos são capazes de armazenar
energia elétrica.
Define-se por polarização um deslocamento reversível dos centros das cargas
positivas e negativas na direção do campo elétrico externo aplicado.
Se o isolante é constituído de átomos, que não apresentam momento dipolar,
quando aplicado um campo elétrico externo, ocorre à separação entre o núcleo
atômico positivo (fixado na matriz do dielétrico) e a nuvem eletrônica, a qual é
deslocada na direção oposta ao campo elétrico aplicado, produzindo dipolos
sem dissipar energia. Uma vez eliminado o campo externo, os átomos voltam à
sua posição inicial, a polarização desaparece, pois os centros de cada grupo de
cargas voltam à situação inicial (equilíbrio).
Se o dielétrico for constituído de partículas elementares (elétrons, prótons, etc.)
que por si só já são dipolos (por exemplo, moléculas) que, devido à sua
constituição química já são dotados de cargas positivas e negativas, a ação do
campo elétrico externo tenderá a orientar as partículas de acordo com a
própria orientação do campo externo. Quanto mais intenso é o campo, tanto
mais elevado é o trabalho de orientação das partículas elementares,
observando-se de modo mais acentuado a elevação de temperatura, devido à
transformação do trabalho de orientação em calor.
c) O que é capacitância?
Capacitância (C): é a razão entre os módulos de sua carga Q e a diferença de
potencial V entre elas. A unidade e Faraday.
d) O que é Constante dielétrica?
Constante dielétrica (ou permissividade) (ε ou k): é uma propriedade do
material isolante utilizado em capacitores que influi na capacitância total do
dispositivo.
Através da constante dielétrica, pode relacionar a densidade de fluxo elétrico e
o campo elétrico do material, quanto maior a constante dielétrica, maior a
densidade de fluxo elétrico no material para um mesmo campo elétrico, maior
a capacitância
e) O que é Rigidez dielétrica?
Rigidez Dielétrica: Corresponde ao valor limite de tensão aplicada sobre a
espessura do material (kV/mm), sendo que, a partir deste valor, os átomos que
compõem o material se ionizam e o material dielétrico deixa de funcionar como
um isolante.
2) Um capacitor cerâmico convencional consegue armazenar 2,1.10-10C de carga
elétrica, possui uma constante dielétrica relativa de 6,0 e está posicionado dentro
da região entre placas a uma tensão de 30V. Calcule a capacitância e a
permissibilidade (constante dielétrica) do meio dielétrico.
: 0 = 8,85.10-12 F/m.
C = Q = 2,1.10-10 = 7,0 .10-12 F
V
30
 =  R .  0 = 6,0 . 8,85.10-12 = 5,31. 10-11F/m
3) Considere um capacitor de placas paralelas que possui uma área de 6,45.10-4m2 e
que apresenta uma separação entre placas de 2.10-3 m, através da qual um
potencial de 10V é aplicado. Se o material que possui uma constante dielétrica
relativa de 6,0 for posicionado dentro da região entre placas, calcule a
capacitância e magnetude da carga armazenada em cada placa
: 0 = 8,85.10-12 F/m.
R =
C=.A
L
 =  =  R .  0 = 6,0 . 8,85.10-12 = 5,31. 10-11F/m
0
= 5,31. 10-11 . 6,45.10-4 m2 = 1,71. 10-11 F
2.10-3 m
C = Q => Q = C.V = 1,71. 10-11 F x 10 V = = 1,71. 10-10 C
V
4) Pretende-se construir um capacitor simples de placas paralelas para armazenar
5,0.10-6 C a um potencial de 8kV. A distância de separação entre as placas é de
0,30mm. Calcule a área em m2 que as placas devem ter, se o dielétrico entre elas
for a) vácuo ( k = 1)
b) alumina ( k = 9)
C = Q = 5,0.10-6 = 6,25 .10-10 F
V
8000
a) C = k  . A = > A = C. L = 6,25 .10-10 x 0,30.10-3
L
k
1x 8,85.10-12
= 0,0212 m2
b)
C = k.  . A = > A = C. L = 6,25 .10-10 F x 0,30.10-3 m
L
k.
9x 8,85.10-12
= 0,0024 m2
5) Qual a definição de um semicondutor, e seu emprego é muito utilizada em qual
ramo da indústria eletrônica.
São sólidos cristalinos
entre condutores e isolantes.
de condutividade elétrica
intermediária
Seu emprego é importante na fabricação de componentes eletrônicos tais
como diodos, transistores e outros de diversos graus de complexidade
tecnológica, microprocessadores, e nano circuitos usados em nanotecnologia.
6) Que tipos de perturbações um semicondutor pode receber para ter uma
influencia na condutividade elétrica?
O valor numérico da condutividade é uma característica definida e
intermediaria entre condutores e isolantes, e também define o comportamento
funcional dos materiais.
A condutividade elétrica de um semicondutor é sensivelmente influenciada
também por eventuais perturbações da estrutura cristalina, o que, por sua vez,
tem fundamental importância nos próprios processos de fabricação dos
semicondutores.
Tais perturbações podem ser provocadas tanto por irregularidades na
estrutura cristalina, pela presença proposital ou acidental de impurezas
(intrínseco e extrínsecos).
7) Demonstre através da distribuição eletrônica de Linnus Pauling os 4 números
quânticos (nível, subnível, orbital e rotação dos elétrons) e mostre também a
representação da banda de Valencia em termo de orbitais dos seguintes
elementos semicondutores:
a) Si (Z = 14)
b) Ge ( Z= 32):
a) n= 3 l = 1 m = 0
s = -1/2
b) n= 4 l = 1 m = 0
s = -1/2
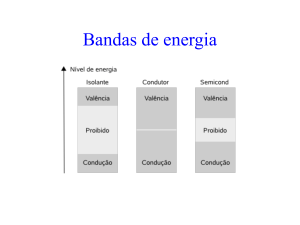
8) Como que funciona a teoria de bandas de energia de um condutor, isolante e um
semicondutor?
Os metais são bons condutores da corrente elétrica não só porque a banda de
valência e a banda de condução se encontram semi-preenchidas, mas também
porque a banda de condução se sobrepõe à banda de valência.
No caso dos isolantes, as bandas de condução e de valência encontram-se
separadas por uma larga zona energética proibida e, deste modo, os elétrons
não possuem energia suficiente para transitar de uma para outra.
No caso dos semicondutores, o nível de energia que separa a banda de energia
superior completamente ocupada possui uma largura muito pequena
relativamente à banda imediatamente superior desocupada, bastando um
pequeno acréscimo de energia para fazer passar os elétrons para a banda
desocupada, possibilitando assim a condução de correntes elétricas.
9) Explique o que é um semicondutor intrínseco, extrínseco tipo P e extrínseco tipo
N?
Um semicondutor intrínseco é um semicondutor no estado puro. À temperatura
de zero graus absolutos (-273ºC) comporta-se como um isolante, mas à
temperatura ambiente (20ºC) já se torna um condutor porque o calor fornece a
energia térmica necessária para que alguns dos elétrons de valência deixem a
ligação covalente (deixando no seu lugar uma lacuna) passando a existir alguns
elétrons livres no semicondutor.
SEMICONDUTORES TIPO N: A introdução de átomos penta valentes (como o
Arsênio) num semicondutor puro (intrínseco) faz com que apareçam elétrons
livres no seu interior. Como esses átomos fornecem (doam) elétrons ao cristal
semicondutor eles recebem o nome de impurezas doadoras ou átomos doadores.
Todo o cristal de Silício ou Germânio, dopado com impurezas doadoras é
designado por semicondutor do tipo N (N de negativo, referindo-se à carga do
elétrons).
SEMICONDUTORES TIPO P: A introdução de átomos trivalentes (como o Índio)
num semicondutor puro (intrínseco) faz com que apareçam lacunas livres no seu
interior.
Como esses átomos recebem (ou aceitam) elétrons eles são denominados impurezas
aceitadoras ou átomos aceitadores.
Todo o cristal puro de Silício ou Germânio, dopado com impurezas aceitadoras é
designado por semicondutor do tipo P (P de positivo, referindo-se à falta da carga
negativa do eletros).
10) Para o silício intrínseco, a condutividade elétrica à temperatura ambiente é de
4.10-4 (.m)-1 ; as mobilidades de elétrons e buracos são respectivamente, de
0,14 e 0,048 m2/V.s. Calcule as concentrações de elétrons livres à temperatura
ambiente.
: e = carga do elétron = 1,6 .10 -19C
n=
11) Qual são os tipos de técnicas de dopagem de um semicondutor:
a) Durante o crescimento boreal, Por fusão, Por implantação iônica, Eletrolise
b) Eletrodeposição, Blindagem iônica, Por liga, nitretação iônica.
c) Durante o crescimento do cristal, Por liga, Por implantação iônica, Por difusão
d) Eletrodeposição eletrólise Valência, liga silício-Germânio
e) Durante o crescimento do cristal, eletrodeposição, Por implantação iônica, fusão
zonal
resposta C
12) Dê um exemplo de um semicondutor que você utiliza em seu trabalho?
=============================================================