Física 121
55
Módulo 49· Equilíbrio de um ponto material
Um corpo será considerado ponto material quando pudermos desprezar o seu tamanho.
Equilíbrio de um ponto material Resultante das forças igual a zero
F1
F3
F2
F1 + F2 + F3 = 0 F R = 0
Exercícios de Aplicação
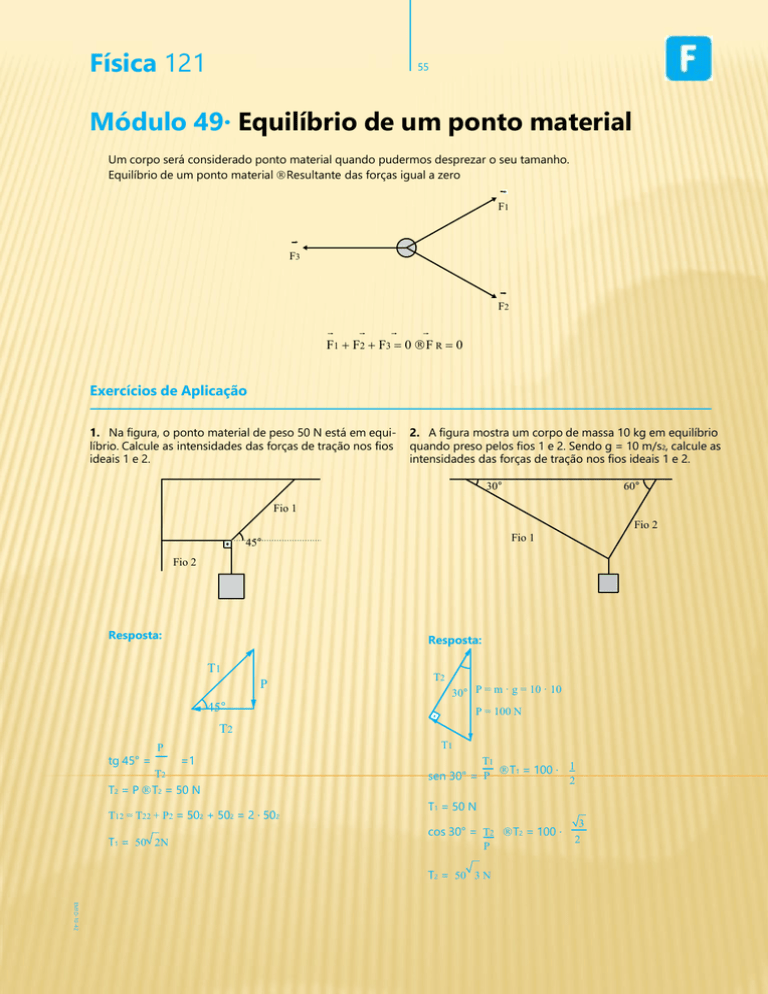
1. Na figura, o ponto material de peso 50 N está em equilíbrio. Calcule as intensidades das forças de tração nos fios
ideais 1 e 2.
2. A figura mostra um corpo de massa 10 kg em equilíbrio
quando preso pelos fios 1 e 2. Sendo g = 10 m/s2, calcule as
intensidades das forças de tração nos fios ideais 1 e 2.
30°
60°
Fio 1
Fio 2
Fio 1
45°
Fio 2
Resposta:
Resposta:
T1
P
T2
30° P = m · g = 10 · 10
45°
P = 100 N
T2
tg 45° =
P
T1
=1
T2
T2 = P T2 = 50 N
T12 = T22 + P2 = 502 + 502 = 2 · 502
T1 = 50 2N
T1
sen 30° = P
T1 = 100 · 1
2
T1 = 50 N
cos 30° = T2 T2 = 100 ·
P
T2 = 50 3 N
3
2
EM1D-10-42
56
Exercícios Extras
4. A figura abaixo mostra um corpo em equilíbrio quando
3. Nafiguraabaixo,oscorposAeBestãoemequilíbrioelivres
preso por dois fios ideais. Nessas condições, calcule as inde atrito. Sendo g = 10 m/s2 e a massa do corpo A igual a 50 kg,
calcule a massa do corpo B. Dados: sen Q = 0,6 e cos Q = 0,8 tensidades das forças de tração nos dois fios.
45°
T1
45°
T2
A
B
P = 100 N
Roteirodeestudos
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo12,itens1e2
Tarefaproposta
Questões577,578,579,580,581,582
Tarefasuplement
ar
Reforço
Questões583,584,585,586
Aprofundamen
to
Questões587,588
Física 121
57
Módulo 50· Momento de uma força
O momento de uma força corresponde à grandeza física
associada ao movimento de rotação de um corpo.
O = ponto de articulação
F
M=±F·d
Os sinais de mais ou menos estão associados ao sentido
de rotação da barra.
Unidades no SI:
u(F) = N
u(d) = m
u(M)= N · m
Momento resultante
d
F
F1
O
F3
O
O ponto de articulação da barra que recebe o nome
de polo da força. Esse ponto representa o ponto em torno do
qual a barra pode realizar o movimento de rotação.
F força aplicada na barra.
d distância do polo ao ponto de aplicação da força.
F4
F2
MR = M1 + M2 + M3 + M4
Exercícios de Aplicação
1. Para fazer uma porta girar, devese aplicar sobre a maçaneta, colocada a
uma distância d da dobradiça, uma força de módulo F perpendicular à porta.
Se a força fosse aplicada a uma distância d da dobradiça dessa porta,
2. Uma chapa retangular, representada na figura abaixo,
possui 40 cm de comprimento e 20 cm de largura. Calcule o
momento da força F em relação ao ponto de articulação O.
F = 20 N
2
calcule, em função de F, a nova intensidade da força aplicada para que o
efeito seja o mesmo que o anterior.
20 cm
0
Resposta:
M1 = M2 F · d = F’ · d
F’ = 2 · F
2
40 cm
Resposta:
M = F · d = 20 · 0,4 M = 8 N · m
EM1D-10-42
58
Exercícios Extras
3. Uma placa retangular está sustentada por um pino em
seu centro O, tendo a possibilidade de girar. Nela são aplicadas três forças, conforme o esquema a seguir.
F2 = 50 N
F1 = 30 N
4. Uma caixa cúbica apresenta aresta de 1 m e massa de
20 kg. Ela se encontra num local em que g = 10 m/s2. Calcule a mínima intensidade da força F, horizontal e aplicada
na aresta superior da caixa, conforme a figura, para que
ela gire (tombe), sabendo que o atrito não permite haver
escorregamento da caixa na superfície.
F
0
20 cm
F3 = 40 N
20 cm
Calcule o momento resultante no centro O dessa placa.
Roteirodeestudos
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo12,itens3e4
Tarefaproposta
Questões589,590,591,592,593,594
Tarefasuplement
ar
Reforço
Questões595,596,597,598
Aprofundamen
to
Questões599,600
Física 121
59
Módulo 51· Equilíbrio de um corpo extenso
Equilíbrio de translação: ocorre quando a resultante das forças aplicadas nesse corpo for igual a zero.
Equilíbrio de rotação: ocorre quando o momento resultante for igual a zero.
N
m1
m2
P
N1
N2
Estando o sistema em equilíbrio de translação, temos:
FR = 0 N = P + N1 + N2
Estando o sistema em equilíbrio de rotação, temos:
MR = 0 MN + MN1 + MN2 + M= 0
Exercícios de Aplicação
1. A figura mostra uma barra homogênea mantida em equi- 2. Uma barra rígida, homogênea e mantida na horizontal
líbrio na horizontal, de peso 200 N, apoiada num suportepossui comprimento de 6 m e peso de 240 N. Uma de suas
e contendo dois blocos fixos nas posições mostradas, cujas extremidades está apoiada num suporte fixo e a outra está
por um fio ideal. Calcule a intensidade da força
massas são m1 = 20 kg e m2 desconhecida. Calcule a massa msustentada
2
para que essa barra permaneça em equilíbrio e a intensidade de tração no fio que sustenta a barra e a intensidade da
da força de reação normal do suporte na barra. Considere os força trocada entre a barra e o suporte.
blocos na iminência de cair da barra. Adote g = 10 m/s2.
m1
2m
m2
6m
Resposta:
MP 1 = MP + MP2
P1 · d1 = P · d + P2 · d2
20 · 10 · 2 = 200 · 1 + m2 · 10 · 4
400 – 200 = 40 · m2
m2 = 5 kg
N = P1 + P2 + P
N = 200 + 200 + 50
N = 450 N
1m
Resposta:
MT = MP T · bT = P · bP
T · 5 = 240 · 3 T = 144 N
N + T = P N + 144 = 240 N = 96 N
EM1D-10-42
60
Exercícios Extras
3. Uma gangorra de comprimento 5 m está sustentada pelo 4. Uma barra rígida, horizontal, de peso 800 N e compriseu centro de gravidade num suporte rígido. Uma criança
mento 5 m encontra-se apoiada em dois suportes, conforme
de massa 25 kg está sentada numa das extremidades daa figura abaixo. Calcule o máximo comprimento X para que
uma criança de massa 20 kg possa ficar em pé sobre a barra,
gangorra. Calcule a que distância do ponto de apoio deve
sentar-se uma pessoa de massa 62,5 kg para que o sistema na extremidade da esquerda, sem correr o risco de a barra
permaneça em equilíbrio sem que os pés de ambas toquem girar. Adote g = 10 m/s2.
o solo.
X
Roteirodeestudos
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo12,item5
Tarefaproposta
Questões601,602,603,604,605,606
Tarefasuplement
ar
Reforço
Questões607,608,609,610
Aprofundamen
to
Questões611,612
Física 121
61
Módulo 52· Exercícios de estática
Resumo
Equilíbrio de um ponto material: FR = 0
Equilíbrio de um corpo extenso: translação: FR = 0
rotação: MR = 0
Exercícios de Aplicação
1. O corpo com peso de 300 N, mostrado na figura abai2. Uma barra rígida de peso 200 N está apoiada em dois
xo, está em equilíbrio quando sustentado por fios e mola
suportes que a mantém em equilíbrio horizontal. Calcule a
ideais. Sabendo-se que a deformação da mola é de 5 cm,
intensidade das forças aplicadas pelos apoios na barra.
calcule a constante elástica dessa mola.
4m
45°
1m
300 N
Resposta:
M2 = MP N2 · d2 = P · d
N2 · 3 = 200 · 2 N2 = 133 N
N1 + N2 = P N1 + 133 = 200
N1 = 67 N
Resposta:
T
P = 300 N
45°
tg 45o = P = 1 F = P = 300 N
F
F = k · x 300 = k · 5 · 10–2
k = 6.000 N/m
Exercícios Extras
3. Uma barra de comprimento 5 m e peso 200 N está sustentada por dois fios ideais, como mostra a figura abaixo.
Nela estão dois corpos de pesos iguais a 100 N cada. Calcule
as intensidades das forças de tração nos fios 1 e 2 que prendem a barra no teto.
4. Dois blocos, A e B, estão apoiados sobre planos lisos,
ligados entre si por uma corda inextensível, sem peso,
que passa por uma polia sem atrito. Sendo mA = 24 kg,
g = 10 m/s2, sen = 0,8 e cos = 0,6, calcule a massa do
bloco B para que o sistema permaneça em equilíbrio.
5m
Fio 1
2m
Fio 2
A
Roteirodeestudos
EM1D-10-42
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo12,itensde1a5
Tarefaproposta
Questões613,614,615,616,617,618
Tarefasuplement
ar
Reforço
Questões619,620,621,622
Aprofundamen
to
Questões623,624
B
62
Módulo 53·Densidade e pressão
1. Pressão
ParaumachapadeáreaAquerecebeaaçãodeumaforçade
intensidade F aplicada perpendicularmente à sua superfície.
3. Densidade (d)
Para um corpo heterogêneo ou oco.
F
m
F
p=
A
d=
V
A
Unidades:
1 atm = 760 mmHg = 76 cmHg = 1,013 · 105 Pa = 10,3 mca
2. Massa específica ()
m
V
Parte vazia
Unidades:
Para uma porção de matéria maciça e homogênea.
1 g/cm3 = 1 kg/d = 103 kg/m3
=
m
m
V
V
Exercícios de Aplicação
1. Durante uma apresentação, uma bailarina de massa
60 kg fica apoiada na ponta de um único pé cuja área de
contato com o solo é de 8 cm2. Considerando o solo plano
e horizontal e g = 10 m/s2, calcule a pressão que o pé da
bailarina troca com o solo.
2. Num recipiente apropriado misturam-se um líquido A,
de volume 40 cm3 e massa 120 g, com outro líquido B, de
volume 200 cm3 e massa 360 g. Calcule a densidade da mistura desses dois líquidos.
Resposta:
p=
N
A=
A
m·g
60 ·10
=
= 7,5 ·105
8 ·104
Resposta:
m = m1 + m2 = 120 + 360 = 480 g
V = V1 + V2 = 40 + 200 = 240 cm3
d=
p = 7,5 · 105 N/m2
m 480
d = 2 g/cm3
V = 240
Exercícios Extras
3. Uma pessoa de massa 100 kg apoia-se sobre uma chapa 4. Dois cubos maciços de ferro são tais que a aresta de um
de aço de 50 cm x 50 cm. Considerando a aceleração da gra- deles é exatamente o triplo da aresta do outro. Calcule a
vidade g = 10 m/s2, calcule a pressão que a chapa exerce no razão entre as massas dos cubos maior e menor.
solo. Considere a massa da chapa igual a 20 kg.
Roteirodeestudos
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo13,itensde1a3
Tarefaproposta
Questões625,626,627,628,629,630
Tarefasuplement
ar
Reforço
Questões631,632,633,634
Aprofundamen
to
Questões635,636
Física 121
63
Módulo 54· Teorema de Stevin
1. Pressão hidrostática
2. Teorema de Stevin
Dado um recipiente cilíndrico e completamente cheio
Dado um líquido contido num recipiente e em equilíde um determinado líquido:
brio, marcaremos dois pontos de alturas diferentes.
A
h
h
No fundo do recipiente, a pressão do líquido é dada por:
phid = · g · h
A pressão total é de:
p = patm + · g · h
Stevin: “A diferença de pressão entre dois pontos de
um líquido em equilíbrio é igual ao produto do desnível (h)
entre esses pontos pela massa específica do líquido e pela
aceleração da gravidade”.
As unidades devem ser apenas do Sistema Internacional.
u(p) = N/m2 = Pa
u(µ) = kg/m3
u(g) = m/s2
u(h) = m
Exercícios de Aplicação
1. Calcule a profundidade que devemos mergulhar num lago2.
Um mergulhador está sujeito a uma pressão total de
contendo água limpa para que a pressão atmosférica aumente1,6 · 105 N/m2. Sendo a pressão atmosférica local igual a
1,0 · 105 N/m2, a massa específica da água 1,0 · 103 kg/m3 e
quatro vezes. Considere g = 10 m/s2, a massa específica da água
a aceleração da gravidade 10 m/s2, calcule a profundidade
1,0 g/cm3 e a pressão atmosférica de 1,0 · 105 N/m2.
do mergulhador.
Resposta:
Resposta:
phid = 4 · patm = 4 · 10 · 105 N/m2
p = patm + gh
phid = gh
1,6 · 105 = 1 · 105 + 103 · 10 · h
4 · 105 = 103 · 10 · h h = 40 m
0,6 · 105 = 104 · h h = 6 m
Exercícios Extras
3. Sabendo que a pressão atmosférica vale 1,0 · 105 N/m2, 4. Um recipiente está cheio de um líquido de massa especalcule quantos metros de profundidade na água a pressão cífica 2,0 g/cm3. Considerando g = 10 m/s2, calcule a difehidrostática é aumentada de uma vez na pressão atmos- rença de pressão entre dois pontos no interior desse líquido
férica. Considere g = 10 m/s2 e a massa específica da água sendo a diferença de altura entre eles igual a 20 cm.
1.000 kg/m3.
Roteirodeestudos
EM1D-10-42
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo13,itens4e5
Tarefaproposta
Questões637,638,639,640,641,642
Tarefasuplement
ar
Reforço
Questões643,644,645,646
Aprofundamen
to
Questões647,648
64
Módulo 55· Experiência de Torricelli
Vácuo
Tubo de vidro
transparente
completamente
cheio de Hg
h = 76 cm
Cuba contendo Hg
Mergulha-se o tubo de mercúrio, após fechado, na cuba.
A seguir, abre-se o tubo.
No nível do mar, a altura da coluna era de 76 cm.
Nível do mar: patm = 76 cmHg = 760 mmHg
patm = gh = 13,6 · 103 · 9,8 · 0,76 = 1,013 · 105 N/m2
patm 105 Pa
Vale a relação:
patm = 1 atm = 76 cmHg = 760 mmHg 105 Pa 10 mca
Exercícios de Aplicação
1. No alto de uma montanha de altitude 3.000 m acima2. Numa cidade localizada a uma grande altitude, a presdo nível do mar, verifica-se que a pressão atmosférica é de são atmosférica é da ordem de 7,0 · 104 Pa, enquanto que,
58 cm de Hg. Expresse essa pressão em unidades do sistema ao nível do mar, a pressão atmosférica é de 1,0 · 105 Pa. Calinternacional.
cule a diferença entre a força exercida pela atmosfera sobre
uma superfície de 20 cm2, ao nível do mar e nessa cidade.
Resposta:
cmHg
Pa
Resposta:
76
1 · 105
Dp = 1 · 105 – 7 · 104 = 3 · 104 Pa
58
p
Dp = DF 3 · 104 =
DF
p = 7,6 · 104 Pa
A
20 ·104
DF = 60 N
Exercícios Extras
3. Numa cidade, acima do nível do mar, a altura da co-4. A pressão atmosférica varia com a altitude de forma que a
luna de mercúrio de um barômetro mede 50 cm. Conside- cada 100 m de altitude a pressão diminui em 1 cmHg. Sabendo
rando g = 10 m/s2 e a massa específica do mercúrio igual
que, no nível do mar, a pressão é de 76 cmHg, calcule a pressão
a 13,6 g/cm3, calcule a pressão atmosférica (em pascal) atmosférica, em Pa, numa cidade situada a 2.000 m de altitunessa cidade.
de. Considere que 76 cmHg corresponda a 1,0 · 105 Pa.
Roteirodeestudos
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo13,item6
Tarefaproposta
Questões649,650,651,652,653,654
Tarefasuplement
ar
Reforço
Questões655,656,657,658
Aprofundamen
to
Questões659,660
Física 121
65
Módulo 56· Vasos comunicantes
Partindo-se do teorema de Stevin, pontos de mesma
altura num mesmo líquido suportam a mesma pressão, en-
Dados dois líquidos imiscíveis, temos:
tão: p1 = p2.
h2
h1
Como: p = patm + · g · h, então:
2
2
1
1
patm + µ1 · g · h1 = patm + 2 · g · h2
µ1 · h1 = 2 · h2
Exercícios de Aplicação
1. A figura abaixo mostra dois líquidos imiscíveis contidos 2. A figura mostra um manômetro de mercúrio em equinum vaso em forma de U. O líquido menos denso possuilíbrio com um recipiente contendo gás. Nessas condições,
massa específica de 2,4 g/cm3. Calcule a massa específicacalcule a pressão do gás, sabendo que a pressão atmosférica
do líquido mais denso.
no local é de 76 cmHg.
12 cm
8 cm
1 2
2
1
h = 60 cm
Gás
Resposta:
d1 · h1 = d2 · h2
d1 · 8 = 2,4 · 12 d1 = 3,6 g/cm3
Resposta:
pgás = patm + phid
pgás = 76 + 60
pgás = 136 cmHg
Exercícios Extras
3. Dois líquidos imiscíveis estão confinados num tubo do- 4. Um manômetro de mercúrio, contendo um tubo de exbrado conforme mostra a figura abaixo. Os líquidos estãotremidade aberta, está conectado a um gás e em equilíbrio,
em equilíbrio. Calcule a razão entre as massas específicas
conforme mostra a figura abaixo. Sendo a pressão atmosdos líquidos contidos no tubo.
férica no local de 70 cmHg, calcule a pressão do gás em Pa.
Adote g = 10 m/s2 se a massa específica do mercúrio igual a
13,6 g/cm3.
20 cm
1
15 cm
Gás
2
20 cm
Roteirodeestudos
EM1D-10-42
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo13,itens7e8
Tarefaproposta
Questões661,662,663,664,665,666
Tarefasuplement
ar
Reforço
Questões667,668,669,670
Aprofundamen
to
Questões671,672
66
Módulo 57· Princípio de Pascal
O acréscimo de pressão dado a um ponto de um líquido ideal e em equilíbrio se transmite integralmente para todos os
pontos desse líquido e das paredes do recipiente no qual ele está contido.
A2
A1
F2
F1
A2
A1
Como Dp1 = Dp2 e p = F , então:F1 = F2
A
A1 A2
F1
d1
F2
d2
F1 . d1 = F2 . d2
Exercícios de Aplicação
1. Uma prensa hidráulica contendo óleo possui dois ramos 2. Uma prensa hidráulica contém dois êmbolos cilíndricos,
de áreas A1 = 5 cm2 e A2 = 20 cm2. No êmbolo de menor área,cujos raios são 10 cm e 40 cm. Se no êmbolo maior for coé aplicada uma força de intensidade 200 N. Calcule a inten- locado um corpo de massa 160 kg, para que a prensa fique
sidade da força que aparece no êmbolo de maior área.
equilibrada, calcule a intensidade da força que deve ser
aplicada no êmbolo menor. (Adote g = 10 m/s2)
Resposta:
Resposta:
F1
F2
200 = F 2 F2 = 800 N
=
A1
A2
5
20
F 1 = F2 F 1
= F2
r2
R2
A1 A2
F 1 = 160 ·10 F1 = 100 N
402
102
Exercícios Extras
3. A figura a seguir mostra uma prensa hidráulica cujos 4. Calcule a relação entre as forças “F” e “f”, aplicadas nos
êmbolos têm áreas S1 = 10 cm2 e S2 = 30 cm2. No êmbolo me-êmbolos da prensa hidráulica da figura, para que o sistenor, aplica-se uma força F de intensidade igual a 100 N para ma permaneça em equilíbrio. O raio do cilindro maior é 10
manter em equilíbrio um corpo de peso P, colocado sobre o (dez) vezes o raio do cilindro menor.
êmbolo maior. Calcule o peso do corpo.
F
F
S1
S2
Roteirodeestudos
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo13,itens9e10
Tarefaproposta
Questões673,674,675,676,677,678
Tarefasuplement
ar
Reforço
Questões679,680,681,682
Aprofundamen
to
Questões683,684
f
Física 121
67
Módulo 58· Força de empuxo (I)
Todo corpo que se encontra mergulhado num líquido está sujeito a uma força, que atua de baixo para cima, denominada
empuxo, cujo módulo é igual ao módulo do peso do líquido deslocado pelo corpo.
E
E = Pd = d · Vd · g
P
Exercícios de Aplicação
1. Numa piscina cheia de água, coloca-se um corpo de massa
2. Uma esfera de raio 20 cm apresenta densidade 2 g/cm3.
1 kg e volume 4 · 10–3 m3. Considerando g = 10 m/s2 e a massaCalcule a intensidade da força de empuxo sobre essa esfera
específica da água igual a 1 · 103 kg/m3, calcule a intensida- quando ela se encontrar totalmente submersa na água, cuja
de da força de empuxo que esse corpo recebe da água.
massa específica é de 1 g/cm3. Adote g = 10 m/s2 e = 3.
Resposta:
Resposta:
dc =
1
mC
=
4 ·103
VC
= 0,25 · 103 kg/m3
VC = 4 · · R3 = 4 · 3 · 0,23 = 3,2 · 10–2 m3
3
dc < µl corpo flutua
E = PC = mc · g = 1 · 10 E = 10 N
3
E = µL · VC · g = 103 · 3,2 · 10–2 · 10
E = 320 N
Exercícios Extras
3. Um cubo maciço apresenta 5,0 cm de aresta e densidade
4,0 g/cm3. Numlocalemqueg=10m/s2,essecuboéabandonadonointeriordeumlíquidocujadensidadeé1,25g/cm3.Calcule a intensidade da força de empuxo pelo líquido no cubo.
4. Um bloco de isopor, de massa específica 0,2 g/cm3 e
volume 2 m3, encontra-se flutuando na água, cuja massa
específica é de 1 g/cm3. Considerando g = 10 m/s2, calcule o
volume do bloco que fica imerso.
Roteirodeestudos
EM1D-10-42
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo13,item11
Tarefaproposta
Questões685,686,687,688,689,690
Tarefasuplement
ar
Reforço
Questões691,692,693,694
Aprofundamen
to
Questões695,696
68
Módulo 59· Força de empuxo (II)
A força normal que o corpo troca com o fundo do recipiente representa o peso aparente desse corpo.
E
N
Pap = N = Pc – E
PC
Exercícios de Aplicação
1. Uma esfera de massa 10 kg e volume 4 · 10–3 m3 encontra-se totalmente mergulhada na água, cuja massa específica vale 1 · 103 kg/m3. Adotando g = 10 m/s2, calcule o peso
aparente dessa esfera.
Resposta:
Pc = mc · g = 10 · 10 = 100 N
E = L · Vc · g = 103 · 4 · 10–3 · 10 = 40 N
Pap = Pc – E = 100 – 40
Pap = 60 N
2. A figura mostra uma barra cilíndrica e homogênea apoiada
num suporte. O corpo, de massa 10 kg e volume 4 · 103 m3,
preso por um fio num dos extremos da barra, encontra-se totalmente imerso num líquido de massa específica 1,5 g/cm3.
Sendo g = 10 m/s2, calcule a intensidade da força F para que a
barra permaneça na horizontal e em equilíbrio.
1m
1m
F
Resposta:
Pc = mc · g = 10 · 10 = 100 N
E = L · Vc · g = 1,5 · 103 · 4 · 10–3 = 60 N
T = Pc – E = 100 – 60 T = 40 N
F = 40 N
Exercícios Extras
3. Um objeto, quando completamente mergulhado na água, 4. A figura mostra uma esfera de massa 20 kg e de mastem um peso aparente igual a três quintos de seu peso real. sa específica 5 g/cm3, totalmente submersa num líquido de
Sendo a densidade da água igual a 1 g/cm3, calcule a den- massa específica 2,0 g/cm3. Um fio vertical sustenta a esfera
sidade desse objeto.
para que ela não toque o fundo do recipiente. Sendo, nesse
local, g = 10 m/s2, calcule a intensidade da força de tração
nesse fio.
Roteirodeestudos
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo13,item12
Tarefaproposta
Questões697,698,699,700,701,702
Tarefasuplement
ar
Reforço
Questões703,704,705,706
Aprofundamen
to
Questões707,708
Física 121
69
Módulo 60· Noções de hidrodinâmica
1. Tensão superficial
Moléculas de um líquido:
Sendo A a área de secção transversal desse tubo, temos:
Z=v·A
3. Equação da continuidade
A figura abaixo mostra dois tubos de diâmetros diferentes conectados entre si. Pelos canos, escoa um líquido.
Tomando uma molécula do meio desse líquido, as forças A1
atuantes são:
A2
d1
Tomando uma molécula da superfície superior desse líquido:
Z1 = Z2
A1 · v1 = A2 . v2
4. Teorema de Torricelli
h
Essa molécula terá uma resultante das forças que as outras moléculas exercem nela para baixo. Essa força gera a
tensão superficial do líquido.
2. Vazão de um líquido
A vazão (Z) é definida pelo volume do líquido que passa
por uma secção desse tubo na unidade de tempo. Assim:
Z= V
d2
v
v2 = v02 + 2 · a · Ds = 0 + 2 · g · h
v = 2· g·h
Dt
Exercícios de Aplicação
1. Por uma torneira aberta, vazam 5 litros de água por minuto. Calcule a vazão dessa torneira em cm3 por segundo.
Resposta:
V = 5 d = 5.000 cm3
Dt = 1 min = 60 s
Z=
V 5.000
=
Dt
60
Z = 83,3 cm /s
3
2. Um reservatório de água possui 80 cm de altura e, na
sua base inferior, encontra-se uma torneira. Considerando g = 10 m/s2 e o reservatório totalmente cheio de água,
calcule a velocidade de saída da água quando a torneira for
aberta. Despreze as dissipações.
Resposta:
v= 2 g h
v = 2 10 0,8 = 16
v = 4 m/s
EM1D-10-42
70
Exercícios Extras
3. Dois tubos de diâmetros 5 cm e 10 cm são conectados um4. Um tanque cilíndrico possui área de base 1 m2 e altura
ao outro. A água passa pelo tubo de menor diâmetro a uma 2 m e encontra-se inicialmente vazio. Uma torneira é ligada
velocidade de 6 m/s. Calcule sua velocidade no tubo de maiorna parte superior desse tanque com o intuito de enchê-lo
diâmetro. Considere os tubos dispostos na horizontal.
de água. Sabendo que a velocidade de saída da água da
torneira é de 0,8 m/s e sua área de secção transversal é
de 2 cm2, calcule o intervalo de tempo gasto para encher
completamente esse tanque.
Roteirodeestudos
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo13,itensde13a16
Tarefaproposta
Questões709,710,711,712,713,714
Tarefasuplement
ar
Reforço
Questões715,716,717,718
Aprofundamen
to
Questões719,720
Física 122
71
Módulo 49· Transformações isobárica e isocórica
1. Descrição macroscópica do gás ideal
1) as moléculas são tratadas como pontos materiais, ou seja, suas dimensões e formas não serão consideradas na
descrição;
2) grande número de moléculas em movimento desordenado (caótico);
3) choques perfeitamente elásticos e de pequena duração entre as moléculas e as paredes do recipiente que as
contém;
4) só são consideradas as forças que agem durante o choque entre moléculas desprezando quaisquer outras interações,
sejam de origens gravitacional ou elétrica.
2. Quantidade de gás
n=
massa do gás
massa molar
=m
M
3. As variáveis de estado de um gás
a) Temperatura (T)
b) Volume ocupado pelo gás (V)
c) Pressão (p)
4. Transformações gasosas
Transformaçãogasosa
Estado1
Estado2
p1
p2
V1
V2
T1
T2
4.1. Transformação isobárica (primeira lei de Charles4.2. Transformação isométrica (segunda lei de Charles
e Gay-Lussac)
e Gay-Lussac)
V = K1T
p
= K2
T
V
= K1
T
Caso a massa se mantenha constante:
V1
= K1
T1
V2
= K1
T2
p1 p
T1 = T22
V1 V2
=
T1 T2
Gráfico da transformação isométrica
p
V
V2
p2
V1
p1
EM1D-10-42
T1
T2
T(K)
T1
T2
T(K)
72
Exercícios de Aplicação
1. Determinada massa gasosa, à temperatura de 27 °C, 2. Com base no gráfico, que representa uma transformação
isovolumétrica de um gás ideal, podemos afirmar que, no
ocupa um volume de 10 d, conforme a figura abaixo.
estado B, a temperatura é de:
p (N/m2)
Êmbolo
Gás
B
4
2
Aquecendo o conjunto e deixando que o êmbolo do recipiente se desloque livremente, a pressão do gás se manterá
0
A
constante enquanto ele se expande. Qual é o volume do gás a) 273 K
quando a temperatura atinge 177 °C?
b) 293 K
c) 313 K
a) 25 d
d) 15 d
b) 20 d
e) 12 d
Resposta: D
c) 18 d
Resposta: D
Estado inicial: V1 = 10 d, T1 = 27 + 273 = 300 K
Estado final: V2 = ?; T2 = 177 + 273 = 450 K
Na transformação isobárica:
V1 V2
=
V2 =
T1 T2
10450
V
300
2
(°C)
20
d) 586 K
e) 595 K
p A VA
p V
= B B
TA
TB
TA = 20 + 273 = 293 K
Como VA = VB, tem -se:
2 = 4
293 TB
= 15
TB = 586 K
Exercícios Extras
3. Em uma cidade brasileira, no horário mais quente do 4. Um gás ideal exerce pressão de 2 atm a 27°C. O gás sofre
dia, um motorista calibrou os pneus de seu carro a uma uma transformação isobárica na qual seu volume sofre um
pressão de 30 lb/in2 (libras por polegada quadrada ou psi), aumento de 20%. Supondo não haver alteração na massa do
usando gás nitrogênio à temperatura ambiente. Contudo, gás, sua temperatura passou a ser, em °C:
a chegada de uma frente fria fez com que a temperaturaa) 32
ambiente variasse de 27 °C para 7 °C, ao final do dia. Consi- b) 54
derando as características do nitrogênio como as de um gás c) 87
ideal e que os pneus permanecem em equilíbrio térmico com d) 100
o ambiente, a pressão nos pneus ao final do dia, devido à
e) 120
variação de temperatura, foi de, aproximadamente:
a) 7 lb/in2
b) 14 lb/in 2
c) 28 lb/in2
d) 30 lb/in 2
e) 32 lb/in2
Roteirodeestudos
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo13,itensde1a4.2
Tarefaproposta
Questões597,598,601,603
Tarefasuplement
ar
Reforço
Questões599,602,605,607,608
Aprofundamen
to
Questões600,604,606
Física 122
73
Módulo 50· Transformação isotérmica e lei geral
1. Transformação isotérmica
(Lei de Boyle-Mariotte)
2. Lei geral dos gases perfeitos
pV
= K4
T
p · V = K3
Como massa e temperatura são constantes:
Se a quantidade de gás permanece a mesma durante o
processo:
p1V1 = p 2 V2
T1
T2
p1 · V1 = p2 · V2
Representação gráfica da lei de Boyle-Mariotte
p
p1
Isoterma
p2
T = constante
V2
V1
V
Exercícios de Aplicação
1. Uma massa de gás ideal sofre a transformação isotérmi- 2. Certa massa de um gás perfeito ocupa o volume de 15
litros a 27 ºC e exerce a pressão de 2 atm. Calcule a pressão
ca A B mostrada na figura:
exercida quando a temperatura passar a 47 ºC e o volume
p (atm)
a 32 litros.
Resposta:
Inicial
V0 = 15 d
T0 = 27 ºC = 300 K
P0 = 2 atm
Hipérbole
2
A
B
1
0
1
VB
V (litros)
Determine o volume VB.
Resposta:
O gráfico hiperbólico mostra que a pressão e o volume
do gás são grandezas inversamente proporcionais. Logo:
pA · VA = pB · VB
2 · 1 = 1 · VB VB = 2 litros
p0V0 = pV
1 1
T1
T0
215 p 32
= 1
300
32010
30
p 1
= 1
300
10
p1 = 1atm
Final
V1 = 32 d
T1 = 47 ºC = 320 K
P1 = ?
EM1D-10-42
74
Exercícios Extras
3. Nas condições p1 = 1,0 atm, T1 = 300 K, certa porção de
gás perfeito ocupa o volume V1 = 12,0 d. Eleva-se a pressão
a p2 = 3,0 atm e a temperatura a T2 = 600 K. O volume passa
a ser:
a) V2 = 8,0 d
b) V2 = 18,0 d
c) V2 = 2,0 d
d) V2 = 36,0 d
e) V2 = 72,0 d
4. Um gás ideal possui um volume de 100 litros e está a
uma temperatura de 27° C e a uma pressão igual a 1 atm
(101.000 Pa). Esse gás é comprimido à temperatura constante até atingir o volume de 50 litros.
a) Calcule a pressão do gás quando atingir o volume de
50 litros.
b) O gás é, em seguida, aquecido a volume constante até
atingir a temperatura de 627 °C.
Calcule a pressão do gás nessa temperatura.
Roteirodeestudos
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo13,itens4.3e5
Tarefaproposta
Questões609,610,611,616
Tarefasuplement
ar
Reforço
Questões612,613,614,615,617
Aprofundamen
to
Questões618,619,620
Física 122
75
Módulo 51· Equação de Clapeyron e mistura de gases
1. Equação de Clapeyron
p · V = n·R·T
Onde :
2. Mistura de gases perfeitos
n=
Para uma situação em que vários gases são misturados
sem que ocorram perdas de massa:
m
M
R = 8,31 J / (mol · K)
pm Vm = p1 V1 + p2 V2 + p3 V
3 +...
Tm
T1
T2
T3
R = 0,082 atm · d / (mol · K)
R 2,0 cal / (mol · K)
Exercícios de Aplicação
1. Num recipiente de 41 litros, são colocados 5,0 mols de
um gás perfeito à temperatura de 300 K. Qual é a pressão
exercida pelo gás nessas condições?
(R = 0,082 atm · d/K · mol)
Resposta:
n = 5,0 mols
V = 41 d
T = 300 K
pV=n·R·T
p=
2. Um gás A, à temperatura T, ocupa um volume de 100 ml
à pressão de 1,0 atm. Um gás B, à temperatura 2 T, ocupa
um volume de 200 ml à pressão de 0,50 atm. Os gases A e
B são misturados, à temperatura 3T, em um recipiente de
500 ml. Calcule a pressão total da mistura.
Resposta:
pV = p A V A + pB VB
T
TA
TB
p500 1100 0,5200
=
+
3T
T
2T
nRT
50,082300
=
V
41
p = 3,0 atm
p = 0,90 atm
Exercícios Extras
3. Um sistema constitui-se de oxigênio (O2), cuja massa
No diagrama da figura anterior, se a temperatura do gás
molecular é 32 g/mol. O mesmo está sofrendo transforma- no estado A é 200 K, que massa de oxigênio está sofrendo
ção no sentido indicado pela seta. Considere que o oxigênio
transformação?
d) 32 g
se comporta como gás ideal (gás perfeito).
a) 2 g
e) 64 g
b)
8
g
joule
Dados: R = 0,082 atmlitro = 8,31
c) 16 g
molK
molK
4. A quantidade de 2,0 mols de um gás perfeito se expande
isotermicamente. Sabendo que no estado inicial o volume
era de 8,20 d e a pressão de 6,0 atm e que no estado final o
volume passou a 24,6 d, determine:
a) a pressão final do gás;
b) a temperatura, em °C, em que ocorreu a expansão.
Dado: constante universal dos gases perfeitos:
R = 0,082 atm · d/mol · K
p (atm)
A
4,1
B
p
2,0
V
V (litros)
Roteirodeestudos
EM1D-10-42
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo13,itens6e7
Leiatambém
MatemáticaeCiênciasdaNatureza4–Capítulo13,Leituracomplementar
Tarefaproposta
Questões621,622,623,625
Tarefasuplement
ar
Reforço
Questões624,626,627,628,631
Aprofundamen
to
Questões629,630,632
76
Módulo 52· Teoria cinética
1. Hipóteses do modelo cinético-molecular
2. Pressão exercida por um gás
I.
O número de moléculas contidas em um recipiente
1
é sempre elevado, sendo que todas são idênticas e com a
p = d v2
3
média
mesma massa.
As moléculas se comportam como pontos materiais.
II.
Onde d representa a densidade absoluta do gás e pode
Dessa maneira, o volume ocupado pelas moléculas é despre- ser calculada por:
zível quando comparado com o volume interno do recipiend= m
te. As moléculas descrevem movimento caótico perpétuo
V
(movimento browniano) e obedecem às leis da mecânica
m = massa total da amostra
newtoniana exercendo forças entre si apenas durante as
colisões.
V = volume total ocupado
III. As paredes do recipiente são consideradas indeformá(v2)média = média aritmética dos quadrados das velocidaveis e sofrem colisões com as moléculas. Entre uma colisão des das moléculas
e outra, o movimento é considerado uniforme.
( )
3. Velocidade quadrática média
vqm =
(v )
2
média
=
3RT
M
Importante: da equação acima, podemos observar que,
para um mesmo gás, a velocidade quadrática média de um
determinado gás é função exclusiva de sua temperatura.
Exercícios de Aplicação
1. A respeito do modelo cinético-molecular, não podemos
afirmar que:
a) o modelo pressupõe um elevado número de moléculas.
b) as moléculas se comportam como pontos materiais.
c) a força de atração-gravitação entre as moléculas é responsável pelo aparecimento da pressão.
d) as paredes do recipiente sofrem colisões com as moléculas.
e) entre uma colisão e outra, o movimento é considerado
uniforme.
Resposta: C
A pressão exercida pelo gás deve-se às colisões que suas
moléculas sofrem com as paredes do recipiente.
2. Em um determinado recipiente, existe uma amostra de
hidrogênio à temperatura de 127 ºC. Considerando o oxigênio como um gás ideal, calcule a velocidade quadrática
média das moléculas da amostra.
Dado: M = 2,0 g/mol e R = 8,31 J/(mol · K)
Resposta:
127 oC = 400 K
vqm = (v2)
vqm =
média
=
38, 31· 400
2·103
vqm 2233 m/s
3 . R. T
M
Física 122
77
Exercícios Extras
3. Considere as seguintes afirmações:
I.
A velocidade quadrática média das moléculas de um
gás ideal depende exclusivamente da temperatura do gás.
As colisões das moléculas entre si criam a pressão
II.
exercida pelo gás sobre a paredes do recipiente.
III. A velocidade quadrática média e o quadrado da velocidade média são sinônimos.
São afirmações corretas:
d) I, II e III.
a) somente I.
e) apenas III.
b) I e II.
c) I e III.
4.
Um gás ideal encontra-se à temperatura de 200 ºC e
sofre uma transformação isotérmica em que sua pressão dobra. Determine a relação entre as velocidades quadráticas
médias antes e depois da transformação.
Roteirodeestudos
EM1D-10-42
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo14,itensde1a4
Tarefaproposta
Questões633,636,637,641
Tarefasuplement
ar
Reforço
Questões634,639,640,642,643
Aprofundamen
to
Questões635,638,644
78
Módulo 53· Energia interna
1. Energia cinética média de uma molécula de gás
(Ec)média = 2 3 kB T
Constante de Boltzmann: kB = 1,38 · 10–23 J/K
2. Energia cinética de um gás
Ec =
3 nRT
2
Observação: a energia cinética total é função exclusiva da temperatura do gás, para um determinado número de mols.
3. Energia interna de um gás (U)
U = Ec =
3 nRT
2
Observação: a energia interna, de determinado número de mols, também é função exclusiva da temperatura do gás.
Exercícios de Aplicação
1. Dentro de um cubo oco de alumínio, existe uma porção
de 3,0 mols de gás hélio sob temperatura de 27 ºC. Dado
que a constante de Boltzmann vale kB = 1,38 · 10–23 J/K e
R = 8,31 J/(mol · K), determine:
a) a energia cinética média por molécula do gás;
b) a energia cinética total do gás;
c) a energia interna da amostra.
Resposta:
a) 27 °C = 300 K
(Ec)média
(Ec)média
(Ec)média
= 3 kB T
2
= 3 1,381023300
2
= 6,211021J
b) E = 3 nRT
c
2
Ec = 3 3,08,31300
2
Ec = 11218,5 J
c) U = Ec = 11218,5 J
2. Um recipiente de alumínio possui, em seu interior, uma
mistura de gás de 60 g de hélio e 80 g de gás argônio à temperatura de 47 ºC. Sabendo que MHe = 4,0 g/mol, MAr = 40 g/mol
e R = 8,31 J/(mol · K), determine:
a) a razão entre as energias cinéticas médias do He e do Ar;
b) a energia interna do sistema;
c) o novo valor da energia interna se 50% vazar sem alteração de temperatura da amostra.
Resposta:
a) Razão = 1
(Ec)média
= 2 3 kB T, como a energia é função exclusiva
da temperatura e os gases estão em equilíbrio térmico, podemos afirmar que a energia cinética de cada um é a mesma. Assim, a razão será 1.
b) Com 60 g de hélio, temos 15 mols e, com 80 g de
argônio, 2 mols. Logo, temos 17 mols no recipiente:
U = 3 nRT
2
U = 3 178,31320
2
U = 67809,6 joules
c) Caso 50% do gás extravase, levará 50% da energia
interna com ele restando apenas metade do valor inicial.
U = 33904,8 joules
Física 122
79
Exercícios Extras
3. O gráfico a seguir representa a transformação gasosa so- 4. Um gás ideal monoatômico sofre a transformação defrida por 4,0 mols de um gás monoatômico de um estado A monstrada a seguir a partir do estado A para o estado B. Determine a diferença de energia interna sofrida por esse gás.
para um estado B.
V (m3)
p (N/m2)
B
7
7,5
3
B
A
A
2,5
0
300
700
T (K)
Determine (dado: R = 8,31 J/(mol·K)):
a) a pressão exercida pelo gás no estado A em N/m2;
b) a variação da energia interna, em joules, nos estados
A e B.
0
Roteirodeestudos
EM1D-10-42
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo14,item5
Tarefaproposta
Questões649,651,652,653
Tarefasuplement
ar
Reforço
Questões645,646,650,654,656
Aprofundamen
to
Questões647,648,655
2
6
V (m3)
80
Módulo 54· Trabalho
1. Trabalho numa transformação gasosa
1.1. Trabalho numa transformação isobárica
e = p · DV
pressão p N/m2
volume V m3
trabalho e N · m joule (J)
Nasexpansões
Nascontrações
Nastransformaçõesemque
Vf=Vi(Ex.:isocórica)
Vf>Vi
Vf<Vi
Vf=Vi
DV>0
DV<0
DV=0
(trabalhomotor)
e>0
Ogásrealizatrabalho.
e<0
(trabalhoresistente)
e=0
(trabalhonulo)
Ogásrecebetrabalho.
Ogásnãorecebenemrealizatrabalho.
1.2. Método gráfico para cálculo do trabalho
• Para uma transformação qualquer:
p
N
A
0 V1
V1
V
2. Trabalho numa transformação cíclica
O trabalho total trocado com o meio exterior é numericamente igual à área interna do ciclo.
Realizaçãodociclo
Sinaldotrabalho
Sentidohorário
e>0(trabalhomotor)
(Ogásrealizatrabalho)
Sentidoanti-horário
e<0(trabalhoresistente)
(Ogásrecebetrabalho)
Física 122
81
Exercícios de Aplicação
1. O volume de um gás varia de 2 litros para 6 litros
sob pressão de 2 atmosferas. Dado que 1 litro = 10–3 m3 e
1 atm = 105 N/m2, determine o trabalho realizado pelo gás,
expresso em joules.
2. Um gás perfeito descreve o ciclo ABCDA como mostra a
figura abaixo. O trabalho, em joules, realizado pelo gás é:
p (N/m2)
Resposta:
DV = 4 d = 4 · 10–3 m3
e = p · DV
e = 2 · 105 · 4 · 10–3
e = 8 · 102 J
6,00
2,00
0
B
C
A
D
1,00
3,00
V (m3)
d) 18,0
e) 20,0
a) 2,00
b) 8,00
c) 15,0
Resposta: B
O trabalho é numericamente igual à área do ciclo:
e =N A
e =b·h
e = (3,00 – 1,00) · (6,00 – 2,00)
e = 8,00 J
Exercícios Extras
3. Um gás ideal sofre uma transformação isobárica à
4. A pressão de um gás ideal varia com o volume de acordo
pressão de 10 N/m2. Qual é o trabalho das forças de prescom o gráfico seguinte.
são durante o deslocamento do pistão, sabendo que o
Calcule o trabalho que o gás troca com o meio durante
volume inicial do gás era de 4 m3 e que o volume final é
a compressão do estado A ao estado B.
de 10 m3?
p (105 N/m2)
A
6
2
0
B
2
Roteirodeestudos
EM1D-10-42
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo15,itens1e2
Tarefaproposta
Questões657,658,661,665
Tarefasuplement
ar
Reforço
Questões659,660,662,667,668
Aprofundamen
to
Questões663,664,666
8
V (10–3 m3)
82
Módulo 55· Variação da energia interna
Variação da energia interna de um gás (DU)
DU = DEc =
3 nRDT
2
Aquecimento
Tfinal>Tinicial
DU>0
Aumentodeenergiainterna
Resfriamento
Tfinal<Tinicial
DU<0
Diminuiçãodeenergiainterna
Tfinal=Tinicial
DU=0
Energiainternapermanececonstante
Temperaturanãovariaouseus
valoresinicialefinalsãoiguais.
Exercícios de Aplicação
1. Uma quantidade de 5 mols de moléculas de um gás 2. Certa massa de gás ideal sofre uma transformação na
perfeito monoatômico sofre uma elevação de 500 °C em qual sua energia interna não varia. Essa transformação é:
sua temperatura. Sendo a constante universal dos gases a) isotérmica.
perfeitos R = 8,31 J/mol · K, determine a variação de
b) isobárica.
energia interna sofrida pelo gás.
c) isométrica.
d) adiabática.
Resposta:
e) inexistente.
DU = 3 nRDT
2
Sendo n = 5 mols, R = 8,31J/molK
DT = 500 °C = 500 K, vem:
DU = 3 58,31500
2
Resposta: A
DU = 0 U = U0 T = T0 (transformação isotérmica)
DU 3,1104 J
Exercícios Extras
3. Dois mols de um gás monoatômico têm sua temperatura 4. Determine o aumento de energia cinética sofrido por
elevada de 27 °C para 227 °C. Se R = 8,3 J/mol · K, calcule
8 mols de gás perfeito, quando sua temperatura aumenta
a variação de energia interna sofrida pelo gás.
10 °C.
Dado: R = 8,3 J/mol · K
Roteirodeestudos
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo15,item3
Tarefaproposta
Questões669,670,671,672
Tarefasuplement
ar
Reforço
Questões673,674,675,676,677
Aprofundamen
to
Questões678,679,680
Física 122
83
Módulo 56· Primeira lei da Termodinâmica
1. Primeira lei da Termodinâmica
Q = e + DU
Q>0
• Ogásrecebeenergiadomeionaformadecalor.
Q<0
• Ogáscedeenergiaparaomeionaformadecalor.
Q=0
• Ogásnãotrocacalorcomoambiente.
e>0
• Ogásrealizatrabalho(sofreexpansão).
e<0
• Ogásrecebearealizaçãodetrabalho(sofrecompressão).
e=0
• Ogásnãorecebenemrealizatrabalho(ovolumeinicialefinalsãoiguais).
DU > 0
• Aumentaaenergiainternadogás,aumentaatemperatura.
DU < 0
• Diminuiaenergiainternadogás,diminuiatemperatura.
DU = 0
• Aenergiainternadogás,noinícioenofinal,éidêntica.Omesmoocorrecomatemperatura.
2. Transformações gasosas
2.1. Transformação isobárica
2.3. Transformação isométrica
Q = (p · DV) + DU
2.2. Transformação isotérmica
Q= e
Q = DU
2.4. Transformação adiabática
Q=0
Exercícios de Aplicação
1. Numa transformação isobárica, o volume de um gás ideal aumentou de 0,2 m3 para 0,6 m3, sob pressão de 5 N/m2.
Durante o processo, o gás recebeu 5 J de calor do ambiente.
Qual foi a variação da energia interna do gás?
a) 10 J
b) 12 J
c) 12 J
d) 2 J
e) 3 J
Resposta: E
Q = 5 J (gás recebe calor)
e = p · DV
e = 5 · (0,6 – 0,2)
e = 2 J e DV > 0 e > 0
DU = Q – e
DU = 5 – 2
DU = 3 J
e = – DU
EM1D-10-42
84
2. Um gás, que se comporta como gás ideal, sofre expansão
sem alteração de temperatura, quando recebe uma quantidade de calor Q = 6 J.
a) Determine o valor DU da variação da energia interna
do gás.
b) Determine o valor do trabalho realizado pelo gás durante esse processo.
Resposta:
a) Expansão isotérmica: T constante
U=
nRT U constante
3
2
DU = 0
b) e = Q – DU
e =6–0
e =6J
Exercícios Extras
3. Julgue as afirmações referentes às transformações sofridas por uma determinada massa de gás perfeito.
I.
Num aquecimento isométrico, o sistema recebe calor
menor que o aumento de sua energia interna.
II.
Numa compressão isotérmica, o sistema recebe trabalho que é integralmente transformado em calor.
III. Numa expansão isobárica, o sistema realiza trabalho
e a energia interna diminui.
IV.
Numa expansão adiabática, o trabalho é realizado às
expensas da energia interna.
corretas:
d) II e IV.
a) São
todas.
e) nenhuma.
b) I e II.
c) III e IV.
4. Submete-se um gás perfeito a uma transformação isométrica, fornecendo-lhe uma certa quantidade de calor.
Nestas condições, pode-se afirmar que:
a) todo calor fornecido ao gás é transformado em trabalho.
b) o número de partículas por unidade de volume aumenta.
c) o gás realiza trabalho, pois a pressão aumenta e o volume é constante.
d) a energia interna permanece constante e o gás realiza
trabalho.
e) a quantidade de calor recebida pelo gás aumenta sua
energia interna.
Roteirodeestudos
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo15,itens4e5
Tarefaproposta
Questões681,683,687,688
Tarefasuplement
ar
Reforço
Questões682,684,685,686,690
Aprofundamen
to
Questões689,691,692
Física 122
85
Módulo 57· Leis das mudanças de estado
Transformações cíclicas
• O trabalho total trocado com o meio exterior é numericamente igual à área interna do ciclo.
• Se o ciclo é percorrido no sentido horário, o trabalho será positivo (o gás realiza trabalho sobre o meio).
• Se o ciclo é percorrido no sentido anti-horário, o trabalho será negativo (o gás recebe trabalho do meio).
• DU = 0
• Q=e
Exercícios de Aplicação
1. Uma determinada massa de gás perfeito executa o ciclo indicado na figura abaixo.
p (N/m2)
5,0 · 103
2. Um gás ideal sofre transformação cíclica, conforme o
gráfico a seguir.
p (N/m2)
B
200
100
1,0 · 103
A
B
C
A
D
C
2
0
0
2,0
6,0
V (m3)
Quais são o trabalho realizado, o calor recebido e a variação de energia interna desse sistema, quando o mesmo
percorre um ciclo?
Resposta:
No ciclo, e = N A (interna)
e=N bh
2
e= (6,0 2,0)(5,0 1,0)103
2
e= 8,0103 J
No ciclo, Tf = Ti DU = 0, assim:
DU = Q – e
0 = Q – 8,0 · 103
Q = 8,0 · 103 J
4
V (m3)
a) Dê o nome das transformações AB, BC, CD e DA.
b) Qual é o trabalho realizado na transformação ABCDA?
c) Qual é o trabalho realizado na transformação AB?
d) Em quais transformações o gás recebeu calor? Em quais
perdeu?
e) Em quais transformações houve aumento da energia interna? Justifique.
f) Qual é a variação da energia interna total do gás?
Resposta:
a) AB isocórica ou isométrica
BC isobárica
CD isocórica ou isométrica
DA isobárica
b) eciclo = N Ainterna
eciclo = 2 · 100 = 200 J
c) AB – isométrica DV = 0 e = 0
d) AB: e = 0, DU > 0, Q > 0 – Recebe calor
BC: e > 0, DU > 0, Q > 0 – Recebe calor
CD : e = 0, DU < 0, Q < 0 – Perde calor
DA : e < 0, DU < 0, Q < 0 – Perde calor
e) AB e BC
f) DU = 0
EM1D-10-42
86
Exercícios Extras
3. O diagrama p x V da figura refere-se a um gás ideal pas- 4. Uma amostra de gás ideal sofre as transformações mossando por uma transformação cíclica através de um sistema tradas no diagrama pressão x volume, ilustrado abaixo.
cilindro-pistão.
p (N/m2)
p (N/m2)
4 · 105
2 · 105
0
A
B
D
C
1,5
4,0
3
1
V (cm3)
A
B
1
a) Qual é o trabalho realizado pelo gás no processo AB?
b) Em que ponto do ciclo a temperatura do gás é menor?
C
5
V (m3)
Observe-o bem e analise as afirmativas abaixo, apontando a opção correta:
a) A transformação AB é isobárica e a transformação BC,
isométrica.
b) O trabalho feito pelo gás no ciclo ABCA é positivo.
c) Na etapa AB, o gás sofreu compressão e, na etapa BC,
sofreu expansão.
d) O trabalho realizado sobre o gás na etapa CA foi de 8 J.
e) A transformação CA é isotérmica.
Roteirodeestudos
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo15,item6
Tarefaproposta
Questões693,698,701,702
Tarefasuplement
ar
Reforço
Questões695,697,699,700,703
Aprofundamen
to
Questões694,696,704
Física 122
87
Módulo 58· Segunda lei da termodinâmica
• Enunciado de Clausius: “O calor não passa, espontaneamente, de um corpo para outro cuja temperatura é maior”.
• Enunciado de Kelvin e Planck: “É impossível construir uma máquina, operando em ciclos, cujo único efeito seja
retirar calor de uma fonte e convertê-lo integralmente em trabalho”.
Exercícios de Aplicação
1. Do segundo princípio da termodinâmica, podemos afirmar que:
a) é possível transformar todo calor em trabalho, sem
ocorrer perdas, com máquinas térmicas operando com duas
fontes de calor em temperaturas diferentes em ciclos.
b) toda máquina térmica possui 100% de rendimento.
c) o rendimento máximo de uma máquina térmica depende do tipo de calor que ela recebe.
d) as máquinas térmicas, operando em ciclos, nunca transformam integralmente, sob forma de trabalho, a energia
que lhe foi cedida sob forma de calor.
e) a energia total de um sistema sempre é constante.
Resposta: D
O segundo princípio afirma que: enunciado de Kelvin
e Planck: “É impossível construir uma máquina, operando
em ciclos, cujo único efeito seja retirar calor de uma fonte
e convertê-lo integralmente em trabalho”.
2. A energia é um dos conceitos da física com aplicação mais
visível no dia a dia. Para mover um carro, por exemplo, é
necessário obter energia através da queima do combustível.
Para os eletrodomésticos funcionarem, depende-se da energia
elétrica. Mas nem toda energia gerada está disponível para
ser transformada em trabalho útil. Para saber quanto dessa
energia pode ser considerada “livre” – disponível para consumo –, é necessário conhecer um outro conceito.
Disponível em:<http:/iwww.cbof.br>. Acesso
em: 20 jul. 2005. Adaptado.
O conceito a que o autor do texto se refere é o de:
a) temperatura, que está relacionado à lei zero da termodinâmica.
b) energia interna, que está relacionado à primeira lei da
termodinâmica.
c) energia interna, que está relacionado à segunda lei da
termodinâmica.
d) entropia, que está relacionado à primeira lei da termodinâmica.
e) entropia, que está relacionado à segunda lei da termodinâmica.
Resposta: E
A primeira lei da Termodinâmica (DU = Q – e) é uma
generalização da conservação de energia. A segunda lei da
Termodinâmica diz que não é possível realizar um processo
cujo único efeito seja produzir trabalho a partir da energia,
na forma de calor.
EM1D-10-42
88
Exercícios Extras
3. De acordo com a segunda lei da termodinâmica, a entropia do universo:
a) não pode ser criada nem destruída.
b) acabará transformada em energia.
c) tende a aumentar com o tempo.
d) tende a diminuir com o tempo.
e) permanece sempre constante.
4. Com base nas leis da termodinâmica, quais das afirmações abaixo são corretas?
I.
O calor não pode passar espontaneamente de um corpo para outro de temperatura mais baixa que o primeiro.
II.
Para produzir trabalho, continuamente, uma máquina
térmica, operando em ciclos, deve, necessariamente, receber
calor de uma fonte quente e ceder parte a uma fonte fria.
III. É impossível construir uma máquina, operando em
ciclos, cujo único efeito seja retirar calor de uma fonte e
convertê-lo em uma quantidade equivalente de trabalho.
IV. É possível se converter totalmente calor em outra forma de energia.
d) Nenhuma.
a) Somente I.
e) Todas.
b) Somente II e III.
c) Somente II e IV.
Roteirodeestudos
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo15,item7
Tarefaproposta
Questões707,710,712,714
Tarefasuplement
ar
Reforço
Questões705,706,711,713,715
Aprofundamen
to
Questões708,709,716
Física 122
89
Módulo 59· Princípio das trocas de calor
1. Máquinas térmicas
3. Potências da máquina térmica
Esquema:
Fonte quente
3.1. Potência útil
TQ
QQ
Pútil = e
t
e
Máquina
térmica
3.2. Potência dissipada
Pdissipada =
3.3. Potência total
QF
Fonte fria
TF
Ptotal =
e = QQ – QF
2. Rendimento da máquina térmica
=
e
H = 1 QF
QQ
Qfria
Dt
QQ
0 H <1
Observações:
• Se H = 0 significa um rendimento de 0%.
• Não é possível que uma máquina térmica, operando
em ciclos, tenha rendimento de 100%; logo, não é possível
que H = 1,0.
Qquente
Dt
Ptotal = Pútil + Pdissipada
Quadro de unidades:
Grandeza
SI
Calor
joule(J)
Trabalho
joule(J)
Potência
joule/segundo(J/s)
1,0watt(W)=1,0J/s
Exercícios de Aplicação
1. Durante um intervalo de 10 segundos, uma máquina
térmica, que operava em ciclos, tem seu comportamento
monitorado. Detectou-se que a máquina retirou 1.600 joules da fonte quente transformando apenas 32% em trabalho, rejeitando todo o restante para fonte fria. Determine,
para este intervalo de tempo:
a) o trabalho realizado;
b) o calor rejeitado para fonte fria;
c) a potência útil da máquina.
Esquematicamente:
Fonte quente
e = 512 J
Máquina
térmica
Resposta:
a) Para calcular o trabalho:
= e
QQ
e
1600
e = 512 J
0,32 =
TQ
QQ = 1600 J
QF
Fonte fria
b) e = QQ – QF
512 = 1600 – QF
QF = 1088 J
EM1D-10-42
e
t
512
Pútil =
10
Pútil = 51,2 W
c) Pútil =
TF
90
2. Uma máquina térmica, operando em ciclos, realiza um trabalho de 800 J em 20 s. Sabendo que durante esse tempo foi
rejeitada, para a fonte fria, 2.000 J, determine, para esses 20 segundos:
a) a potência útil da máquina;
b) o rendimento da máquina.
Resposta:
a) Calculando
a potência útil:
e
b) QQ = e + QF
Pútil =
QQ = 800 + 2000
t
800
Pútil = 20
QQ = 2800 J
e
= QQ
Pútil = 40 W
800
= 2800
= 0,29 ou 29 %
Exercícios Extras
4. A respeito das máquinas térmicas, são feitas as afir3. Uma máquina térmica, operando conforme o esquema
mações:
abaixo,
retira,
fontecalquente,
12.000 caltodo
por ociclo
e rejeita,
para
fonte
fria,da
4.800
transformando
restante
de I.
Uma máquina térmica precisa apenas de uma fonte
calor em trabalho. Determine o rendimento da máquina.
quente para retirar calor e transformar em trabalho.
II.
Com o aperfeiçoamento das máquinas, já é possível
Fonte quente
TQ
encontrar máquinas térmicas com rendimento de 100%
(que não sofram perdas).
QQ
III. O trabalho realizado em cada ciclo é a diferença entre o
calor retirado da fonte quente e o rejeitado para fonte fria.
São corretas:
a) somente a I.
e
b) somente a II.
Máquina
c) somente a III.
térmica
d) I e II.
e) II e III.
QF
Fonte fria
TF
Roteirodeestudos
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo15,itensde8a10
Leiatambém
MatemáticaeCiênciasdaNatureza4–Capítulo15,Aprofundamento
Tarefaproposta
Questões718,719,720,722
Tarefasuplement
ar
Reforço
Questões717,723,724,725,727
Aprofundamen
to
Questões721,726,728
Física 122
91
Módulo 60· Ciclo de Carnot
O ciclo de rendimento máximo é denominado ciclo de
Carnot.
p
Adiabática 2
Em resumo, o ciclo de Carnot, que representa uma máquina térmica em rendimento máximo, consta de duas
transformações adiabáticas alternadas e duas isotérmicas.
• AB e CD são isotérmicas.
• BC e DA são adiabáticas.
Adiabática 1
• TQ é a temperatura da fonte quente.
• TF é a temperatura da fonte fria.
• O trabalho realizado será dado pela expressão e = QQ – QF.
A
B
Isotérmica TQ
D
C
QF
T
= F
QQ
TQ
Isotérmica TF
H = 1
V
QF
QQ
H = 1
TF
TQ
Exercícios de Aplicação
1. Uma máquina térmica funciona realizando o ciclo de 2. O gráfico a seguir representa um ciclo de Carnot, para
Carnot. Em cada ciclo, o trabalho útil fornecido pela má- o caso de um gás ideal. Assinale, dentre as seguintes, a
quina é de 2.000 J. As temperaturas das fontes térmicas são proposição falsa.
227 °C e 27 °C, respectivamente. Determine:
p
a) o rendimento da máquina;
b) a quantidade de calor retirada da fonte quente;
A
c) a quantidade de calor rejeitada para a fonte fria.
Resposta:
T1 = 227 + 273 = 500 K
T2 = 27 + 273 = 300 K
B
D
C
T2
a) H = 1 T1
H = 1 300
500
H = 40%
b) = e
Q1
0,4 = 2.000
Q1
Q1 = 5.000 J
c) Q1 = e + Q2
5.000 = 2.000 + Q2
Q2 = 3.000 J
0
V
a) De A até B, a transformação é isotérmica e o gás recebe
calor do meio externo.
b) De C até D, a transformação é isotérmica e o gás rejeita
calor para o meio externo.
c) De B até C, a transformação é adiabática e o gás realiza
trabalho contra o meio externo.
d) De D até A, a transformação é adiabática e o gás realiza
trabalho contra o meio externo.
e) Durante o ciclo, o trabalho realizado pelo gás sobre o
meio externo é maior que o trabalho realizado pelo meio
externo sobre o gás.
Resposta: D
De D para A: compressão adiabática. O volume diminui
e, portanto, o meio realiza trabalho contra o gás.
EM1D-10-42
92
Exercícios Extras
3. O rendimento de certa máquina térmica de Carnot é de
25% e a fonte fria é a própria atmosfera a 27 °C. A temperatura da fonte quente é:
a) 5,4 °C
b) 52 °C
c) 104 °C
d) 127 °C
e) 227 °C
4. Com relação a máquinas térmicas, considere as afirmativas abaixo:
I.
O rendimento de uma máquina térmica pode ser
de 100%.
II.
O rendimento de uma máquina de Carnot depende das
temperaturas das fontes fria e quente.
III. Existe, pelo menos, uma máquina térmica que, operando entre as fontes de calor às temperaturas T1 e T2, tem
rendimento superior ao de uma máquina de Carnot que
opere entre estas temperaturas.
Está(ão) correta(s) apenas:
a) I.
b) II.
c) III.
d) I e II.
e) II e III.
Roteirodeestudos
Leiacomatenção
MatemáticaeCiênciasdaNatureza4–Capítulo15,item11
Leiatambém
MatemáticaeCiênciasdaNatureza4–Capítulo15,Leituracomplementar
Tarefaproposta
Questões730,732,735,736
Tarefasuplement
ar
Reforço
Questões729,733,734,737,740
Aprofundamen
to
Questões731,738,739
Resoluções
93
Física 121
Módulo 49
3.
T = PB
T = PA · senQ
o
senQ =
sen o 90 cos – sen · cos90
P = P · senQ
B
1
A
mB · g = mA · g · sen Q
mB = 50 · 0,6 mB = 30 kg
4.
T1 = T2 = T
T2 + T2 = P2 2 · T2 = P2
2 ·T=P T=
100
2
·
2
2
mA· g · sen = mB · g · cos
24 · 0,8 = mB · 0,6
mB = 32 kg
Módulo 53
3.
T1 = T2 = 50 2 N
P=
N (m1 +m2) g
=
A
0,5 0,5
1.200 = 4.800
P = (100 + 20) 10 =
0,25
0,25
Módulo 50
P = 4.800 N/m
3.
MR = – F1 · d1 + F2 · d2 – F3 · d3
MR = – 30 · 0,1 + 50 · 0,1 – 40 · 0,1 = – 3 + 5 – 4
MR = – 2 N · m
4.
MF = MP F · a = P ·
F=
2
=
P
4.
a
2
=
m2
2
m
m = V
V
=
V2
m1
= 27
m2
20 ·10
2
0
senQ = cos
F = 100 N
m1
= a3
V1
a=3
(3a)3
Módulo 51
Módulo 54
3.
M1 = M2 P1 · d1 = P2 · d2
m1 · g · d1 = m2 · g · d2 25 · 2,5 = 62,5 · x
x=1m
3.
Phid = µ · g · h
1 · 105 = 1.000 · 10 · h h = 10 m
4.
4.
M1 = M2 P1 · d1 = P2 · d2
20 · 10 · x = 800 · (2,5 – x)
200 x = 2.000 – 800 x
1.000 x = 2.000
x=2m
p2 = p1 + · g · h
p2 – p1 = 2 · 103 · 10 · 0,2
DP = 4 · 103 N/m2
Módulo 52
3.
M1 = Mp1 + Mp
T1 · dT1 = P1 · d1 + P · dp
T1 · 5 = 100 · 3 + 200 · 2,5
T1 = 160 N
T1 + T2 = P1 + P2 + P
160 + T2 = 100 + 100 + 200
T2 = 240 N
4.
T = PA · sen
T = PB· senQ
P sen
= P senQ
A
B
senQ = sen (90o – )
Módulo 55
3.
patm = m · g · h
patm = 13,6 · 103 · 10 · 0,5
patm = 6,8 · 104 Pa
4.
2.000 m 76 – 20 = 56 cmHg
cmHg
Pa
76
1 · 105
56
p
p = 7,4 · 104 Pa
Módulo 56
3.
d1 · 20 = d2 · 15
d1 3
=
d2 4
27a3
EM1D-10-42
94
4.
pgás = patm + phid
pgás = 70 + 20 = 90 cmHg
pgás = · g · h = 13,6 · 103 · 10 · 0,9
pgás = 1,22 · 105 Pa
4.
Z=
f
F
f
F
=
r2
A2
R
=
A1
2
3.
C
Considerando uma transformação isométrica, V = cte,
tem-se:
4.
VC = (5 · 10–2)3 = 125 · 10–6 m3
E = L · VC · g = 1,25 · 103 · 125 · 10–6· 10
E = 1,56 N
mC = 400 kg
3.
Módulo 59
Pap =
3
Pc
5
5
mc
1103 =
dc =2,5 103 kg/m3
2 Vc
mc
dc =
5103 =
Vc
V0
T =
V0
V
VT0
V0
Módulo 60
v1 · A1 = v2 · A2
v1 · · r12 = v2 · · r22
6 · 2,52 = v2· 52
v2 = 1,5 m/s
A
Inicial
p1 = 1,0 atm
T11 =
V
= 300
12,0Kd
Final
p2 = 3,0 atm
T2 = 600 K
V2 = ?
3V2
V2 = 4 · 2
V2 = 8,0 d
4.
20
Vc = 4103 m3
Vc
Pc = mc · g = 20 · 10 = 200 N
E = L · Vc · g = 2 · 103 · 4 · 10–3 · 10 = 80 N
T = Pc – E = 200 – 80
T = 120 N
3.
T =
112
300 = 600
Pap = Pc E 3 P = Pc E
5 c
2
2
E = 5 Pc L Vc g =5 mc g
4.
T
Módulo 50
2
E = PC L · Vs · g = mC · g
1 · 103 · Vs = 400 Vs = 0,4 m3
3.
=
T = 360 K
Q = 87 °C
dc = mC
0,2 · 103 = mC
p2 = 28 psi
C
p0 = 2 atm; Q0 = 27 °C = 300 K; V0
V = V0 + 20% V0 = 1,2 V0; T = ?
Transf. isobárica:
T0
VC
2
p1 p
30 psi
p2
= 2
=
T1
T2
(27 + 273) (7 + 273)
Módulo 58
4.
V
Dt
Módulo 49
f
F
F
=
= 100
r2 (10r)2
f
3.
1,6 · 10–4 =
Física 122
100
P
F 1 F2
=
=
10
30
A1 A2
P = 300 N
4.
Dt
Dt = 12.500 s
Módulo 57
3.
Z = V · A = 0,8 · 2 · 10–4
Z = 1,6 · 10–4 m3/s
a)
b)
p1 V1 = p2 V2 p2 = 100 = 2 atm
50
2·(627 + 273)
p2 p3
A volume constante:
=
p3 =
(27 + 273)
T2
T3
p3 = 6 atm
Módulo 51
3.
C
p·V=n·R·T
4,12,0 = n0,082200
n = 0,5 mol
m
n = m 0,5 =
M
32
m = 16 g
30012 V0
Resoluções
4.
a)
p1V1
=
p2 V2
T1
T2
68,2 = p2 24,6
95
4.
O trabalho é numericamente igual à área sob a curva
no diagrama p × V.
e =N A
e = (B +b)h
2
(6 + 2)(8 2)105 103
e=
2
p2 = 2 atm
b)
p·V=n·R·T
6 · 8,2 = 2 · 0,082 · T
T = 300 K = 27 °C
Módulo 52
3.
A
I. Correta: Para um mesmo gás ideal, a velocidade
quadrática média das moléculas depende exclusivamente
da temperatura.
II. Incorreta: As colisões entre as moléculas e as paredes do recipiente geram a pressão do gás.
III. Incorreta: Velocidade quadrática média e quadrado da velocidade média são conceitos diferentes.
e = 2,4103 J
O sinal é negativo, pois ocorre a compressão do gás
(DV < 0).
eAB = – 2,4 · 103 J
Módulo 55
3.
4.
Como a velocidade quadrática média é função exclusiva da temperatura e na transformação apresentada
ela permanece constante, podemos dizer que a velocida4.
de quadrática média antes e depois da transformação são
iguais.
Módulo 53
3.
DT = 200 °C = 200 K
DU = 3 nRDT
2
DU = 3 28,3200
2
DU = 4.980 J
DEC = DU =
3
nRDT
2
DEC = 3 88,310
2
DEC = 996 J
A pressão pode ser obtida pela equação de Clapeyron:
Módulo 56
p·V=n·R·T
p · 3 = 4 · 8,31 · 300
3.
p = 3324 N/m2
D
Calculando a variação da energia interna entre os esI.
Errada.
tados A e B:
DU = Q – e, com e = 0 (DV = 0)
DU = Q
UA = 3 nRTA
II. Correta.
2
Compressão isotérmica: DU = 0
UA = 3 48,31300
Q= e
2
III.
Errada.
UA = 14958 J
Expansão isobárica: e > 0
UB = 3 nRTB
o gás realiza trabalho, pois V2 > V1.
2
T2 > T1, portanto a energia interna aumenta.
3
UB = 48,31700
IV. Correta.
2
Expansão adiabática: Q = 0
UB = 34902 J
DU = – e
(DV > 0)
DU = UB UA DU = 19944 J
4.
DU = zero
4.
Pelo gráfico, concluímos que se trata de uma transformação isotérmica, logo, não ocorre variação de temperatura e, consequentemente, a diferença entre as energias
internas entre os estados A e B será zero.
Módulo 54
3.
e = p · DV
EM1D-10-42
e = 10 · (10 – 4)
e = 60 J
E
Transformação isométrica: DV = 0
e =0
U = Q – e
0
DU = Q
Módulo 57
3.
a)
eAB = pA · (VB – VA) = 4 · 105 ·(4 · 10–6 – 1,5 · 10–6)
eAB= 1,0 J
b) No estado em que o produto p · V é menor, isto é,
em D.
96
4.
D
4.
C
I) Errada. Em essência, toda máquina térmica necessita de duas fontes para operar: uma fonte quente, de onde
se retira calor, e outra, a uma temperatura mais baixa, a
chamada fonte fria, para onde se rejeita o calor que não
pôde ser transformado em trabalho.
II) Errada. Pelas leis da Termodinâmica não é possível
Módulo 58
construir uma máquina térmica operando em ciclos que tenham rendimento de 100% ou superior.
3. C
Nos processos físicos, a entropia dos sistemas isolados
III) Correta. O trabalho realizado em cada ciclo é a di3 +1
4
eCA =
2
eCA = 8 J
sempre aumenta.
4.
B
Comentando os itens:
I) Falsa. Essa afirmação contraria a lei de equilíbrio
térmico. O calor flui espontaneamente dos corpos quentes
ferença entre o calor retirado da fonte quente e o rejeitado
para fonte fria.
Módulo 60
3.
para os corpos frios.
II) Correta. A máquina térmica retira calor da fonte
quente e doa parte para a fonte fria.
III) Correta. É o que afirma o segundo princípio da
termodinâmica.
IV) Falsa. É impossível fazer essa conversão para máquinas que operem em ciclos.
T2
n = 1 T1
0,25 = 1 (27 + 273)
T1
0,25 1= (300)
T1
0,75T1 = 300
T1 = 400 K
Módulo 59
3.
D
QF
H = 1
QQ
4800
H = 1
12000
H = 0,6 ou 60%
QC + 273 = T
QC = 400 273
QC = 127 °C
4.
B
I.
Falsa.
H < 100% (Segunda lei)
II. Verdadeira.
III. Falsa.
Hcarnot é máximo.










