Slide 1 - nordesttino

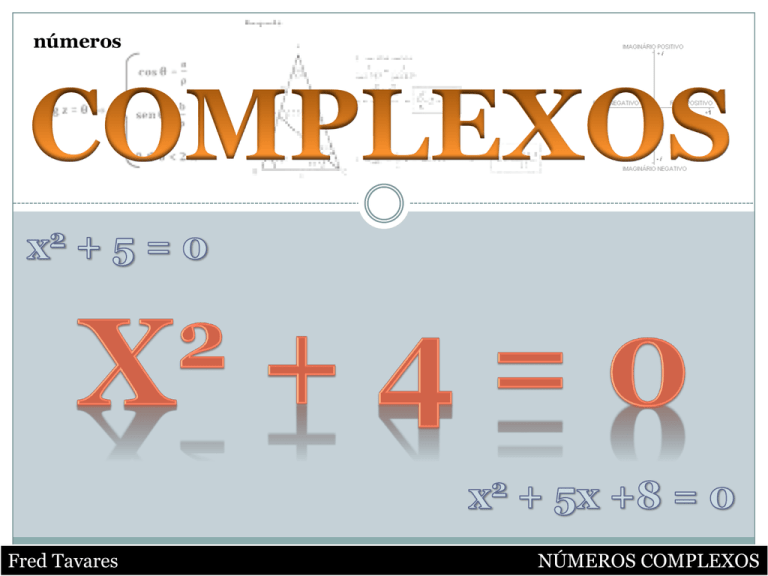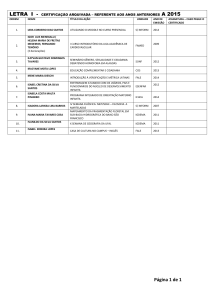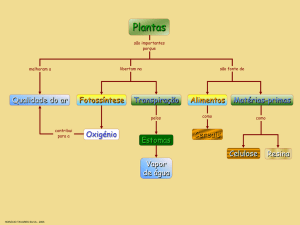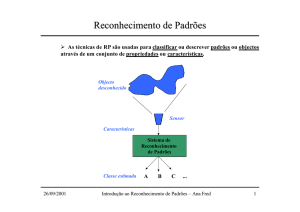
números
Fred Tavares
NÚMEROS COMPLEXOS
NÚMEROS COMPLEXOS
Os números Complexos constituem o maior
conjunto numérico existente.
N: conjunto dos números Naturais
Z: conjunto dos números Inteiros
Q: conjunto dos números Racionais
I: conjunto dos números Irracionais
R: conjunto dos números Reais
C: conjunto dos números Complexos
Fred Tavares
NÚMEROS COMPLEXOS
Os números Complexos constituem o maior
conjunto numérico existente.
Fred Tavares
NÚMEROS COMPLEXOS
Os números complexos são escritos na sua forma
algébrica da seguinte forma:
a + bi, sabemos que a e b são números reais
e que o valor de
a é a parte real do número complexo e que o valor de
bi é a parte imaginária do número complexo.
Podemos então dizer que um número
complexo z será igual a a + bi (z = a + bi).
Com esses números podemos efetuar as operações de
adição, subtração e multiplicação, obedecendo à ordem
e características da parte real e parte imaginária.
Fred Tavares
NÚMEROS COMPLEXOS
OBSERVAÇÕES
2
i
= -1
i = imaginário
Re = real
Im = imaginário
Fred Tavares
NÚMEROS COMPLEXOS
IDENTIFICANDO
Veja alguns exemplos de como identificar a parte real e a
parte imaginária de um número complexo:
z = - 3 + 5i
z = -5 + 10i z = 1/2 + (1/3)i
Re(z) = -3
Re(z) = -5
Re(z) = 1/2
Im(z) = 5
Im(z) = 10
Im(z) = 1/3
Fred Tavares
NÚMEROS COMPLEXOS
As coordenadas a e b podem assumir qualquer
valor real, dependendo do valor que eles assumirem o número complexo
irá receber um nome diferente:
Quando a e b forem
diferentes de zero
dizemos que o
número complexo é
imaginário:
z = 3 + 8i
Quando o valor de a
é igual a zero e o de b
é diferente de zero
dizemos que o
número complexo é
imaginário puro:
z = 0 + 9i
z = 9i
Quando a diferente
de zero e b igual a
zero dizemos que o
número complexo
será real.
z = 7 – 0i
z=7
É comum vir em provas de vestibular.
Fred Tavares
NÚMEROS COMPLEXOS
Exemplos:
Determine o valor de m para que z
=(m-2) + 5i, seja:
Número Real
Para que o complexo seja um número real devemos fazer
b = 0 e a ≠ 0.
m–2≠0
então: m ≠ 2
Imaginário puro
Para que um número complexo seja imaginário puro
a = 0 e b ≠ 0, então podemos dizer que:
m–2=0
então: m = 2
Fred Tavares
Adição
NÚMEROS COMPLEXOS
Dado dois números complexos quaisquer
z1 = a + bi e z2 = c + di, ao adicionarmos teremos:
z1 + z2 = (a + bi) + (c + di) = (a + c) + (b + d)i
Portanto, z1 + z2 = (a + c) + (b + d)i.
RESUMINDO:
REAL COM REAL – IMAGINÁRIO COM IMAGINÁRIO
Fred Tavares
Adição
NÚMEROS COMPLEXOS
Exemplo:
Dado dois números complexos
z1 = 6 + 5i e z2 = 2 – i, calcule a sua soma:
z1 + z2 = (6 + 5i) + (2 – i) =
6 + 2 + 5i – i =
8 + (5 – 1)i =
8 + 4i
Portanto, z1 + z2 = 8 + 4i.
Fred Tavares
Subtração
NÚMEROS COMPLEXOS
Dado dois números complexos quaisquer
z1 = a + bi e z2 = c + di, ao adicionarmos teremos:
z1 - z2 = (a + bi) - (c + di) = (a - c) + (b - d)i
Portanto, z1 - z2 = (a - c) + (b - d)i.
RESUMINDO:
REAL COM REAL – IMAGINÁRIO COM IMAGINÁRIO
Fred Tavares
Subtração
NÚMEROS COMPLEXOS
Exemplo:
Dado dois números complexos
z1 = 6 + 5i e z2 = 2 – i, calcule a sua soma:
z1 - z2 = (6 + 5i) - (2 – i) =
6 - 2 + 5i + i =
4 + (5 + 1)i =
4 + 6i
Portanto, z1 - z2 = 4 + 6i .
Fred Tavares
NÚMEROS COMPLEXOS
Multiplicação
Dado dois números complexos quaisquer
z1 = a + bi e z2 = c + di, ao multiplicarmos teremos:
z1 . z2 = (a + bi) . (c + di) (regra do chuveirinho)
ac + adi + bci + bdi2 = ac + adi + bci + bd (-1)
ac + adi + bci – bd = ac - bd + adi + bci
(ac - bd) + (ad + bc)i (agrupar termos semelhantes)
Portanto, z1 . z2 = (ac + bd) + (ad + bc)i.
Fred Tavares
NÚMEROS COMPLEXOS
Exemplo: SEMPRE PRESTAR ATENÇÃO NO i2
Dado dois números complexos
z1 = 5 + i e z2 = 2 - i, calcule a sua multiplicação:
(5 + i) . (2 - i)
5 . 2 – 5i + 2i – i2
10 – 5i + 2i – (-1)
10 + 1 – 5i + 2i
11 – 3i
Portanto, z1 . z2 = 11 – 3i.
Fred Tavares
Potência i
NÚMEROS COMPLEXOS
A letra i acompanha a parte imaginária e dependo do valor de sua potência
ela irá assumir um valor que irá facilitar vários cálculos.
i 0 = 1, pois todo
i 4 = i2 . i2 = -1 . (-1) = 1
número ou letra
elevando à zero é um.
i 1 = i, pois todo número
elevado a 1 é ele mesmo.
i 2 = -1
i 3 = i2 . i = -1 . i = - i
i 5 = i4 . i = 1 . i = i
i 6 = i4 . i2 = 1 . (-1) = -1.
i 7 = i4 . i3 = 1 . (-i) = - i.
E assim por diante.
Fred Tavares
NÚMEROS COMPLEXOS
RESUMINDO:
AS POTÊNCIAS SEMPRE SE
REPETEM DE
4 EM 4.
Qualquer potência maior que 4,
basta dividir por 4 e pegar o resto.
Fred Tavares
Potência i
NÚMEROS COMPLEXOS
Para descobrir, por exemplo, qual era o valor
da potência i243, basta dividirmos 243 por 4,
o resto será 3 então i243 será o mesmo que i3,
portanto i243
= i3 = - i.
Fred Tavares
Forma algébrica
y
Z = a + bi
b
P
a
NÚMEROS COMPLEXOS
Os números complexos são
formados por um par
ordenado (a, b) onde os
valores de a estão situados
no eixo x (abscissa) e os
valores de b no eixo y
(ordenadas). Sobre o eixo x
marcamos
os
pontos
relacionados à parte real do
número complexo e sobre o
eixo
y
os
pontos
relacionados
à
parte
imaginária.
x
Fred Tavares
NÚMEROS COMPLEXOS
Oposto, conjugado
Oposto
( Basta multiplicar por -1)
O oposto de qualquer número real é o seu simétrico, o oposto
de 10 é -10, o oposto de -5 é +5. O oposto de um número
complexo respeita essa mesma condição, pois o oposto do
número complexo z será – z.
Por exemplo:
Dado o número complexo
z = 8 – 6i, o seu oposto será: - z = - 8 + 6i.
Fred Tavares
NÚMEROS COMPLEXOS
Oposto, conjugado
Conjugado
( Basta mudar o sinal da parte imaginária)
Para determinarmos o conjugado de um número
complexo, basta representar o número complexo
através do oposto da parte imaginária.
O conjugado de z = a + bi será
z = a - bi
Fred Tavares
NÚMEROS COMPLEXOS
Fred Tavares
NÚMEROS COMPLEXOS
Fred Tavares
NÚMEROS COMPLEXOS
Fred Tavares
NÚMEROS COMPLEXOS
Fred Tavares
NÚMEROS COMPLEXOS
Fred Tavares
NÚMEROS COMPLEXOS
Fred Tavares
 Eu Sei Que Vou ESTUDAR
 by Fred e Tavares
 Eu sei que vou ESTUDAR
Por toda a minha vida eu vou ESTUDAR
Em cada NOTA BAIXA eu vou APANHAR
Desesperadamente, eu sei que vou CHORAR
E cada ERRO meu será
Prá ME LEMBRAR que eu sei que DEVO ESTUDAR
Por toda minha vida
Eu sei que vou MELHORAR
A cada NOTA BOA eu vou GRITAR
Mas cada NOTA BAIXA há de LEMBRAR
O que esta CHINELADA me causou
Eu sei que vou sofrer a eterna desventura de viver
A espera de ESTUDAR ao lado teu
PROFESSOR da minha vida