Slide 1 - WordPress.saturniz

GEOMETRIA PLANA
TEOREMA DE TALES
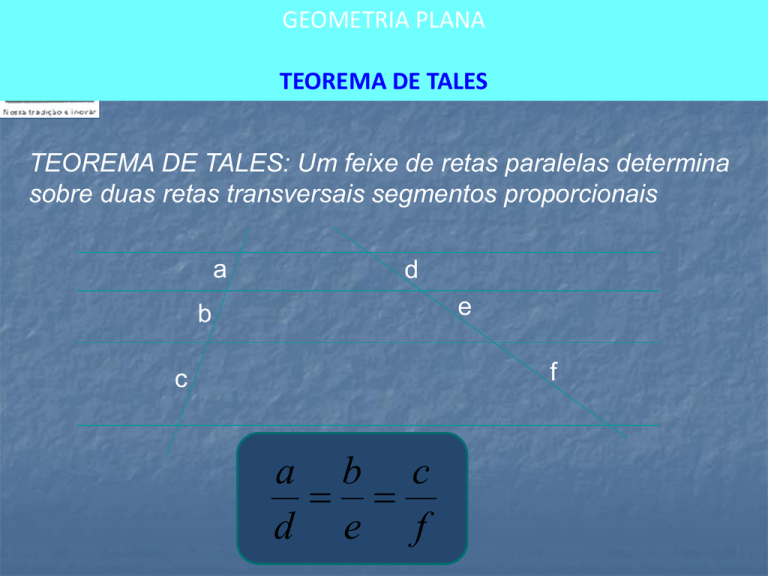
TEOREMA DE TALES: Um feixe de retas paralelas determina
sobre duas retas transversais segmentos proporcionais
a
d
e
b
f
c
a b c
 
d e f
ÁREA DAS PRINCIPAIS FIGURAS PLANAS
5.1. TRIÂNGULOS
TRIÂNGULO QUALQUER:
b.h
A
2
h
b
TRIÂNGULO EQUILÁTERO:
l
l
l
FÓRMULA DE HERON:
b
c
A  p.( p  a).( p  b).( p  c)
a
*p = semi-perímetro
l 2. 3
A
4
5.1. TRIÂNGULOS
DADO UM ÂNGULO:
A
b
C
c
a
B
1
A  .a.b.senC
2
5.1. TRIÂNGULOS
TRIÂNGULO QUALQUER INSCRITO NUMA CIRCUNFERÊNCIA:
a.b.c
A
4 .R
5.1. TRIÂNGULOS
TRIÂNGULO QUALQUER CIRCUNSCRITO NUMA CIRCUNFERÊNCIA:
a.r b.r c.r
A


2
2
2
a.r  b.r  c.r
A
2
(a  b  c)
A
.r
2
A  p.r
*p = semi-perímetro
5.2. PARALELOGRAMOS
D.d
A
2
Retângulo
A  b.h
Quadrado
Paralelogramo
Losango
5.3. TRAPÉZIOS
h
Trapézio
(B  b)
A
.h
2
OBSERVAÇÃO:
Em qualquer polígono regular, a área é dada por:
A = p.a
*p = semi-perímetro
a = apótema
5.3. TRAPÉZIOS
OBSERVAÇÕES:
a) Tipos de Trapézios
Trapézio Escaleno
Trapézio Isósceles
Trapézio Retângulo
5.3. TRAPÉZIOS
OBSERVAÇÕES:
b) Base Média
C
D
c) Mediana de Euler
M
A
E
F
AB  CD
EF 
2
N
B
5.3. TRAPÉZIOS
OBSERVAÇÕES:
d) Diagramas
Quadriláteros
Trapézios
Paralelogramos
Quadrados
INSCRITOS
6.1. Triângulo Eqüilátero
INSCRITOS
6.2. Quadrado
l. 2
r 
2
l
a
2
S l2
INSCRITOS
6.3. Hexágono regular
R. 3
a
2
R2. 3
S  6.
4
CIRCUNSCRITOS
A  p.r
*p = semi-perímetro
OBSERVAÇÕES:
a) Os ângulos opostos de um quadrilátero inscrito são
suplementares.
o
ˆ
ˆ
C  D  180
OBSERVAÇÕES:
b) Se um quadrilátero é circunscrito a uma circunferência, a
soma de dois lados opostos é igual a soma dos outros dois
lados.
b
a
a+c=b+d
c
d
Questão 2:
Determine a medida y, na figura abaixo, sabendo que x + z = y
e que r//s//t//u.
a) 8
b) 9
c) 10
d) 12
e) 14
Solução:
y–3=9
y = 12
Questão 4:
(UFPI) A área do quadrado ABCD inscrito no triângulo
retângulo DEF abaixo é:
a) 42,25cm2
b) 36cm2
c) 46,24cm2
d) 39,32cm2
e) 49cm2
Solução:
10
15

10  l l
10.l  150  15.l
25.l  150
l6
A  l2
A  62
A  36 cm 2
Questão 5:
A figura abaixo mostra uma circunferência de raio 6cm inscrita
em um trapézio retângulo. Calcule a área desse trapézio.
a) 110cm2
b) 120cm2
c) 130cm2
d) 140cm2
e) 150cm2
Solução:
r = 6cm
10cm
12cm
( B  b)
A
.h
2
(15  10)
A
.12
2
A  150 cm 2
Questão 8:
(UFBA/95) Num triângulo ABC, o lado AB mede 1 u.c., o lado
BC 3 u.c. e o ângulo B mede 30º. Assim, pode-se afirmar:
0 0 O perímetro do triângulo mede 5 u.c.
1 1 O triângulo é obtusângulo.
2 2 O triângulo é isósceles.
3 3 A medida da área do triângulo é u.a.
4 4 A altura do triângulo, relativa ao lado AB, mede u.c.
Solução:
A
1
1/2
1x
30o
B
3
Lei dos Cossenos
2
x  1  3  2.1. 3. cos 30o
2
2
3
x 1  3  2. 3.
2
x2  1 3  3
2
x2  1  x  1
0X
0 O perímetro do triângulo mede 5 u.c.
X 1 O triângulo é obtusângulo.
1
X
2 2 O triângulo é isósceles.
X
3 3 A medida da área do triângulo é 3/4 u.a.
4X
4 A altura do triângulo, relativa ao lado AB,
C
mede 2/2 u.c.
b.h
A
2
1
3.
2
A
2
3
A
4
b.h
A
2
3 1.h

4
2
3
h
2
Questão 9:
(COVEST/2005) Uma propriedade rural tem a forma do
triângulo ABC representado na figura. A região cultivada
corresponde apenas à porção sombreada. Sabendo-se que AD
= AB e AE = AC, que porcentagem da área da propriedade
rural é cultivada?
a) 50%
b) 60%
c) 66%
d) 75%
e) 1/2.(2/3 + 3/4).100%
Solução:
Aprop.
y
Acult.

3/4.x
x
Acult.
1
 .x. y.sen
2
1 3 2
 . .x. . y.sen
2 4 3
1
 .x. y.sen
4
Acult.  50% . Aprop.
Questão 12:
(UPE 2003)
0 0 Se a medida da base de um triângulo aumenta 20% e a
medida da altura diminui 30%, a área do triângulo diminui em
16%.
1 1 Três segmentos de medidas 5cm, 6cm e 10cm determinam
um triângulo obtusângulo.
2 2 O apótema de um hexágono regular de lado  é .3
3 3 A medida da hipotenusa de um triângulo retângulo, inscrito
em uma circunferência de raio 2 u.c., é 2.3 u.c.
4 4 A bissetriz de um ângulo interno de um triângulo divide o
lado oposto em segmentos proporcionais.
Solução:
X
0 0 Se a medida da base de um triângulo aumenta 20% e a
medida da altura diminui 30%, a área do triângulo diminui em
16%.
b.h
A
2
1,2.b.0,7.h
b.h
'
A 
 0,84.
2
2
Solução:
X
1 1 Três segmentos de medidas 5cm, 6cm e 10cm determinam
um triângulo obtusângulo.
10 2  52  6 2
100  25  36
100  61
Solução:
2X
2 O apótema de um hexágono regular de lado  é .3
ap 
ap
l
l. 3
2
Solução:
3X
3 A medida da hipotenusa de um triângulo retângulo, inscrito
em uma circunferência de raio 2 u.c., é 2.3 u.c.
2
2
Solução:
X
4 4 A bissetriz de um ângulo interno de um triângulo divide o
lado oposto em segmentos proporcionais.
Teorema da Bissetriz Interna
A
AB
B
P
C
BP

AC
PC
Questão 13:
(COVEST 2003) A razão entre a área do triângulo e a área do
círculo inscrito, ilustrados na figura abaixo, é:
12
a)

6
b)

18
c)

4
d)

1
e)

Solução:
b.h
At 
2
4.3
At 
2
At  6
At  p.r
(3  4  5)
6
.r
2
r 1
Ac   .r 2
Ac   .12
Ac  
At 6

Ac 
Questão 14:
(U.F.Uberlândia-MG/adaptada) Calcule a área de um triângulo
retângulo em que um dos catetos mede 5 cm e o raio da
circunferência inscrita mede 2cm.
a) 20cm2
b) 25cm2
c) 30cm2
d) 40cm2
e) 50cm2
Solução:
(3  x) 2  52  (2  x) 2
3 cm
3 cm
x
2 cm
2 cm
x
9  6.x  x 2  25  4  4.x  x 2
2.x  20  x  10 cm
b.h
A
2
12.5
A
2
A  30 cm 2
Questão 15:
(UFAC) A figura representa um trapézio cujas bases AB e DC
medem 6dm e 10dm. Sendo M e N pontos médios dos lados
AD e BC, conclui-se que a medida do segmento PQ é:
a) 3dm
b) 2dm
c) 3,1dm
d) 2,8dm
e) 3,2dm
Solução:
Mediana de Euler
(10  6)
PQ 
2
PQ  2 dm
Questão 16:
Em um triângulo retângulo ABC a hipotenusa BC mede 15cm e
o cateto AB mede 9cm. Calcule a distância do baricentro G à
reta AC.
a) 1cm
b) 2cm
c) 3cm
d) 4cm
e) 5cm
Solução:
9 cm
4,5 cm
12 cm
2
d  .4,5
3
d  3 cm
Questão 18:
(UFMT) No hexágono regular ABCDEF inscrito
circunferência de raio 4cm, a medida da diagonal FB é:
a) 6cm
b) 6,8cm
c ) 4 3cm
d) 6 2cm
e) 15cm
na
Solução:
Si  (n  2) x180o
120o
2 cm
4 cm
Si  (6  2) x180o
Si  720o
30o
Questão 19:
Um quadrado ABCD e um triângulo eqüilátero EFG estão
inscritos na mesma circunferência de raio 6 cm de modo que
AB//EF, conforme a figura. Calcule a distância entre os lados
AB e EF.
a) 3.( 2  2 )
b) 2.( 3  2 )
c ) 3.( 3  3 )
d) 2.( 2  3 )
e) 3.( 2  3 )
Solução:
r  apq . 2
6. 2  apq . 2
apq  6 cm
Solução:
d  apq  apt
apt  3. 2 cm
r  6. 2 cm
d  6  3. 2
d  3.(2  2 )