F228_AulaExp_5_Oscilacoes

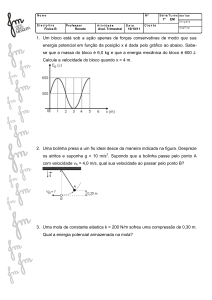
Oscilações
Curso de Física Geral F-228
20 semestre, 2011
Exercício 1
Um bloco de massa m desliza sem atrito sobre um plano inclinado que faz um ângulo θ=30º com a
horizontal e tem uma mola fixa no final da rampa. O bloco é solto de uma posição inicial tal que a
distância entre a ponta livre da mola e a face do bloco é L. Quando o bloco bate na mola, um
dispositivo é acionado conectando o bloco na mola. O bloco comprime a mola até um valor
máximo igual a L, quando a velocidade instantânea do bloco vai a zero. Considere um eixo x ao
longo do plano inclinado no sentido descendente e com sua origem na posição da ponta livre da
mola quando ela não está deformada. Determine, em função dos parâmetros fornecidos e da
aceleração da gravidade g no local:
a) A freqüência angular do MHS que o bloco executa após se conectar à mola.
b) A posição x0 na qual a velocidade do bloco é máxima
c) A posição xm mais alta que o bloco alcança após se conectar à mola
h
Exercício 2
No sistema bloco-mola da figura abaixo, o bloco possui uma massa de 2kg e a mola possui massa
desprezível. O sistema está sobre uma superfície sem atrito que faz um ângulo de 30º com a
horizontal.
a) Sabendo que quando o sistema está em equilíbrio estático a mola sofre uma elongação de
5cm, calcule a constante k da mola.
b) Em seguida, a mola é puxada mais 4cm e depois solta em t=0s. Encontre a freqüência angular
ω, o período T
c) Determine a equação de movimento, velocidade e aceleração
d) Suponha agora que tenha um atrito que exerce uma força F= –b(dx/dt) no sistema. Sabendo
que nesta nova situação o período do movimento é 2s, encontre o valor da constante de
amortecimento b
Utilize g = 10 m/s2 e π = 3 em todos os itens
5cm
0
4cm
x
Exercício 3
Um bloco, preso firmemente a uma mola, oscila verticalmente com uma freqüência de 4Hz e uma
amplitude de 7cm. Uma bolinha é colocada em cima do bloco oscilante assim que ele chega ao
ponto mais baixo. Suponha que a massa da bolinha seja tão pequena que seu efeito sobre o
movimento do bloco seja desprezível. Utilize g = 10 m/s2 e π = 3 em todos os itens.
a) Para qual deslocamento, a partir da posição de equilíbrio
(y0), a bolinha perde o contato com o bloco?
b) Qual a velocidade da bolinha neste momento?
c) A que altura ela chega?
d) Fazendo t=0 no momento em que a bolinha se desprende
do bloco, em quanto tempo depois ela toca no bloco de
novo? Em que posição a partir de y0?
y ( m)
y
t (s)
Exercício 4
A figura abaixo mostra a posição de um bloco de 20g oscilando em um MHS na extremidade de
uma mola. A escala do eixo horizontal é definida por ts=40ms. Quais são:
a) A equação de movimento do bloco
b) A energia cinética, potencial e total do bloco
c) O número de vezes por segundo que esse máximo é atingido?
d) A sua velocidade
e) O módulo da aceleração radial de uma partícula no movimento circular uniforme
correspondente
Máximo em t=0s
A  7cm
 0
T  ts  40ms
x0  0cm
x  t   A cos t     x0
x  t   0.07 cos  50 t 
l
g
  sin   0     2  0
l
Para pequenas oscilações:
  IL  I  mgb sin 
mgb
 I  mgb   
 0
I
2
   2  0
mgb
2
I
 
T 
 2
I

mgb
Exercício 5
A figura abaixo mostra um disco homogêneo de raio R=0.80m, 6.00kg de massa e com um
pequeno furo distante d do centro do disco, que pode servir como ponto de suspensão.
a) Qual deve ser a distância d, para que o período deste pêndulo físico seja 2.50s?
b) Qual deve ser a distância d para que este pêndulo físico tenha o menor período possível?
c) Quanto vale este menor período possível?
1

2
I

mR
 disco
2

 I  I  md 2
CM

1
mR 2  md 2
T  2 2
mgd
R 2  2d 2
 T  2
2 gd
d 2  1.55d  0.32  0