1.a Aula_N5CV1_Circuitos Magnéticos

Conversão de Energia I
N5CV1
Prof. Dr. Cesar da Costa
1.a Aula: Circuitos Magneticos
1. Circuitos Magnéticos Lineares
Definições:

Um circuito magnético linear consiste em uma estrutura que, em sua maior
parte, é composta por material magnético de permeabilidade baixa.

A presença de um material de alta permeabilidade tende a fazer com que o
fluxo magnético seja confinado aos caminhos delimitados pela estrutura, do
mesmo modo que, em um circuito elétrico , as correntes são confinadas aos
condutores.
 Permeabilidade Magnética é uma grandeza magnética, representada por µ
(letra minúscula grega), que permite quantificar o “valor” magnético de uma
substância. A sua unidade é H/m (henry por metro).
1. Circuitos Magnéticos Lineares
Definições:
 Permeabilidade Magnética elevada é uma característica dos circuitos
magnéticos lineares.
 A permeabilidade Magnética no vácuo é dada por:
 A permeabilidade Magnética
dos materiais magnéticos lineares
apresentam valores típicos entre 2.000 e 80.000 H/m.
 A permeabilidade Magnética para efeito de cálculo de projetos é dada
por:
1. Circuitos Magnéticos Lineares
Fig. 1- Circuito magnético simples
1. Circuitos Magnéticos Lineares
• Consideremos o dispositivo da fig. 1, onde o núcleo é formado por um material
de permeabilidade magnética  .
• Pela aplicação da lei de Ampère a este circuito teremos:
(1)
• Considerando que H, intensidade do campo magnético, possui módulo
constante ao longo do caminho médio L, percorrido pelo fluxo magnético 
, mostrado na figura teremos:
(2)
(3)
1. Circuitos Magnéticos Lineares
• O produto N I é o responsável pela condução do fluxo no circuito magnético,
desempenhando o papel de uma fonte. Daí ele ser conhecido por força
magneto motriz (Fmm).
• A relação entre a intensidade de campo magnético H e a densidade de fluxo
magnético B é uma propriedade do material, em que se encontra o campo
magnético. Costuma-se supor que:
B  H
(4)
Substituindo-se o valor de H, obtido na Eq. (3), tem-se:
B
NI
L
(5)
1. Circuitos Magnéticos Lineares
• O fluxo magnético  que passa através da secção reta A , ao longo do
circuito magnético será:
  BA
(6)
• Substituindo-se pelo valor da densidade de fluxo B, obtida
na Eq. (5), tem-se:

 NI A   Fmm A
L
L
(7)
1. Circuitos Magnéticos Lineares
• Ou ainda, o fluxo

 pode ser representada como:
Fmm

(8)
• Onde o termo  do denominador é dada por:
 L
A
(9)
• É chamado de relutância do circuito magnético. Ele representa a
dificuldade imposta à circulação do fluxo magnético.
2. Circuitos Elétricos
• Considere agora o circuito elétrico da fig. 2 formado por um único laço ou
malha de corrente.
Fig. 2 – Circuito elétrico simples
• Para esse circuito elétrico temos a resistência oposta à corrente elétrica dada
por:
L
R
A
(10)
2. Circuitos Elétricos
Onde:
I V
R
(11)
• Portanto, para a corrente elétrica, sendo V a Fem (Força eletromotriz)
responsável pela corrente I, tem-se:
Fem
I  Fem 
R
L /( A)
(12)
• Podemos então montar um circuito elétrico análogo ao circuito
magnético, conforme as correspondências entre as grandezas
magnéticas e elétricas apresentadas na Tabela 1.
2. Circuitos Elétricos
Tabela 1.
Resumo das Fórmulas:
a) Força Magneto Motriz (Fmm)
b) Fluxo Magnético no núcleo
Resumo das Fórmulas:
c) Relutância
d) Permeância
Resumo das Fórmulas:
e) Intensidade de Campo Magnético no Núcleo
f) Densidade de Fluxo Magnético no Núcleo
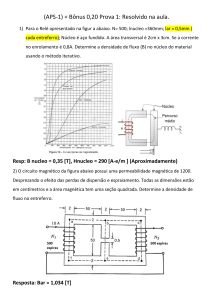
Exercício 1:
Para o dispositivo da fig. 1, tem-se uma corrente I = 5 A, através de N = 100
espiras, fazendo
circular um fluxo magnético por um retângulo cujos
comprimentos médios da base e da altura são respectivamente 10 cm e 8 cm e
secção reta de 2 cm , feito de um material de permeabilidade relativa
r = 1000. Calcular:
2
a) - A relutância do circuito magnético
b) - A permeância do circuito magnético
c) - A intensidade de campo magnético no núcleo
d) - A densidade de fluxo magnético no núcleo
e) - O fluxo magnético no núcleo
Solução 1:
a) Relutância do circuito magnético:
b) Permeância do circuito magnético:
c) Intensidade de campo magnético:
Solução 1:
d) Densidade do fluxo magnético no núcleo:
e) Fluxo magnético no núcleo:
Exercício 2:
Calcular o valor do fluxo magnético em cada braço da estrutura magnética da fig.
3. Dados: N = 500 espiras, I = 1,0 A, material 1 com  r1 = 200 e
material 2 com  r2 = 100. Secão reta é igual a 4 cm2.
Figura 3 - Estrutura ferromagnética do exercício 2
Solução 2:
Circuito elétrico equivalente
Circuito magnético
Material 1:
N .I  H1.l1
Material 2:
N .I  H 2 .l2
Solução 2:
No caso:
l1  l2  lm
lm  (5  5  5  5  2  2  2  2  2  2  2  2)cm  36 cm
N .I 500 1
H1 

 1388,88 A.esp / m
l1
0,36
N .I 500 1
H2 

 1388,88 A.esp / m
l2
0,36
Solução 2:
Inducao magnética no braco esquerdo:
B1  r1 .0 .H1  200  4 107 1388,88  0,34T
Inducao magnética no braco direito:
B2  r2 .0 .H1  100  4 107 1388,88  0,17T
Fluxo magnético no braco direito:
1  B1.A1  0,34  4.104  1,36 104Wb
Fluxo magnético no braco esquerdo:
2  B2 .A 2  0,17  4.104  0, 68 10 4Wb
3. Circuitos Magnéticos Não-Lineares
 São considerados não lineares todos os circuitos magnéticos que utilizem
materiais ferromagnéticos, dotados de permeabilidade magnética alta, tais
como o ferro fundido, o aço silício, o aço fundido, a ferrite etc.
 A maioria dos circuitos magnéticos de aplicação prática são não - lineares e a
permeabilidade dos materiais ferromagnéticos torna-se variável em função da
indução ou densidade de fluxo magnético B no núcleo.
Exercício 3:
As dimensões da estrutura magnética na fig. 4 estão indicadas na tabela em
seguida. O enrolamento de excitação possui 100 espiras. Determine a corrente
neste enrolamento para estabelecer um fluxo de 1.5x10-4 (Wb). Despreze a
dispersão do fluxo magnético, considerando-o todo confinado ao núcleo. Utilize as
curvas de magnetização mostradas a seguir:
Figura 4 - Estrutura ferromagnética
Figura 5 - Circuito elétrico análogo
Solucão 3:
A estrutura mostra um circuito com os dois materiais em série:
Fmm  N .I  H1.l1  H 2 .l2
1  2    1,5 104Wb
  B1. A1  B2 . A2
Como A1 é igual a A2, temos:

1,5 104
2
B1  B2  

0,1
Wb
/
m
A 15 104
Solucão 3:
Das curvas de magnetizacão temos:
a) Para o ferro fundido:
B1  0,1 Wb / m2  H1  225 A.esp / m
b) Para o aco - silício:
B2  0,1 Wb / m2  H 2  35 A.esp / m
Portanto, a corrente I será dada por:
H1.l1  H 2 .l2
I
N
H1.l1  H 2 .l2 225, 0, 2  35.0, 4
I

 0,59 A
N
100
Exercício 4:
Considere a estrutura magnética em aço fundido mostrada na fig. 6. Para um fluxo
magnético de 1,5 x 10-4 Wb, qual é o valor de B nos pontos 1 e 2, dados que S1 =
16 cm2, S2 = 20 cm2, L1 = 15 cm, L2 = 30 cm. Determine também a corrente na
bobina sabendo-se que ela possui 200 espiras.
Figura 6 – estrutura ferromagnética do exercício 4
Solucão 4:
O fluxo magnético é o mesmo em qualquer secão. Logo:
  1  2
A inducão magnética na secão 1:

1,5 104
B1  
 0, 094T
4
A1 16 10
A inducão magnética na secão 2:

1,5 104
B2 

 0, 075T
4
A2 20 10
Solucão 4:
Da curva de magnetizacão para o aco fundido tem-se:
B1  0, 094T  H1  85 A.esp / m
B2  0, 075T  H 2  65 A.esp / m
Sabendo-se que:
N .I  H1.l1  H 2 .l2
H1.l1  H 2 .l2 85  0,15  65  0,3
I

 0,16 A
N
200
4. FATOR DE EMPACOTAMENTO (OU FATOR DE LAMINAÇÃO)
 Quando um material ferromagnético é colocado na presença de um campo
magnético variável no tempo, correntes parasitas (ou correntes de Foucault)
serão induzidas em seu interior, provocando perdas de energia com o
aquecimento do material.
 A redução deste fenômeno é obtida com o núcleo de dispositivos
eletromagnéticos construído com chapas ou lâminas de material
ferromagnético, isoladas entre si (por exemplo, com verniz), conforme pode
ser ilustrado na fig. 7.
Fig. 7 – Núcleo Laminado
4. FATOR DE EMPACOTAMENTO (OU FATOR DE LAMINAÇÃO)
 Assim, devido ao processo de empilhamento das chapas para montagem do
núcleo, a área efetiva do material ferromagnético, Amag atravessada pelo fluxo
torna-se menor que a área geométrica, Ageom ocupada pelo núcleo. Pode-se
então definir um fator de empacotamento ke como sendo a relação:
(13)
 Outra razão de natureza prática para a laminação do circuito magnético é
a de facilitar a colocação das bobinas no dispositivo visando à construção
e a manutenção.
4. FATOR DE EMPACOTAMENTO (OU FATOR DE LAMINAÇÃO)
 A tabela a seguir fornece alguns valores para o fator de empacotamento
em função da espessura da chapa ou lâmina utilizada.
(13)
Exercício 5:
Uma estrutura magnética é feita de um pacote em aço-silício com chapas de
0,15 mm, como pode ser mostrada na fig. 8. Determine a corrente que deve
circular no enrolamento com 500 espiras para estabelecer um fluxo de 9x10-4
Wb no braço direito da estrutura. Dados: L1 = L3 = 50 cm, L2 = 15 cm,
espessura comum A = 25 cm2.
Figura 8 - Estrutura magnética do exercício 5
Solução 5:
Dado:
Como:
Considerando um fator de empacotamento:
Malha 1:
(I)
Como:
Malha 2:
(II)
Nó 1:
(III)
Tem-se:
Solução 5:
Da curva de magnetização para aço silício:
A partir da equação II na malha 2:
Malha 1:
(I)
Malha 2:
Da curva de magnetização para aço silício:
(II)
Nó 1:
(III)
Solução 5:
Da equação III:
Malha 1:
(I)
Da curva de magnetização para aço silício:
Malha 2:
Da equação I:
(II)
Nó 1:
(III)
Corrente no enrolamento:
4.1 CIRCUITOS MAGNÉTICOS COM ENTREFERROS
 Alguns dispositivos eletromagnéticos, tais como instrumentos de medidas,
motores, relés etc, por serem constituídos de uma parte fixa e outra móvel,
possuem um espaço de ar, com comprimento Lg, na sua estrutura
magnética.
 Este espaçamento ou interstício promove o acoplamento entre as partes sob
o ponto de vista magnético para que o fluxo se estabeleça por um caminho
fechado. A este espaço é dado o nome de “entreferro" (ou "air gap" em
inglês).
Figura 9 - Estrutura magnética com entreferro
4.1 CIRCUITOS MAGNÉTICOS COM ENTREFERROS
 Ao cruzar o entreferro, o fluxo magnético sofre um fenômeno chamado de
espraiamento (frangeamento, espalhamento, efeito de bordas), conforme pode
ser visto da fig. 10. Isto faz com que a área efetiva por onde passa o fluxo se
torne maior que a área A geométrica do entreferro.
Campo magnético em um entreferro:
Fig. 10
 Seja uma área de secção reta A = a x b retangular e o entreferro de
comprimento lg. Então, de uma forma prática, podemos calcular a área
aparente ou efetiva do entreferro Ag, através da relação:
(14)
Exercício 6
Vamos investigar a influência de um entreferro sobre um circuito magnético.
Imagine uma estrutura retangular em aço silício, com secção reta de 5 cm x 2 cm,
comprimento médio de 50 cm, excitada por uma bobina de 100 espiras.
Determinar os valores de corrente necessários para que sejam estabelecidos
fluxos magnéticos de 3x10-4 Wb, 6x10-4 Wb e 9x10-4 Wb. Em seguida, admita
um entreferro de 1 mm na estrutura e refaça os cálculos para encontrar os
mesmos valores de fluxo. Analise os resultados.
Solução 6:
2) Para
Sem entreferro:
1) Para
Da curva de magnetização do açosilício:
3) Para
O valor da corrente será:
Com entreferro:
Área efetiva do entreferro:
2) Para
1) Para
A nova corrente com entreferro será
dada por:
Com entreferro:
A partir dos resultados podemos
observar que:
3) Para
a) Para se obter os mesmos
valores de fluxo, com a introdução
do entreferro, é necessário um
aumento muito grande nos valores
da corrente.
b) Praticamente toda a Fmm é
utilizada para vencer o entreferro
(torna-se mais acentuado quanto
maior o entreferro)
c) A introdução do entreferro
tornou o circuito magnético
(material magnético + entreferro)
praticamente linear.
Exercício 7
Considere uma estrutura magnética construída com chapas de aço silício, com
fator de empacotamento 0,9. As dimensões da seção transversal do núcleo são 5
cm e 6 cm. O comprimento médio do caminho do fluxo é 1 m. Determine a Fmm
para estabelecer um fluxo de 25x10-4 Wb no entreferro, cujo comprimento tem 5
mm.
Solução 7:
Indução magnética no entre ferro:
Intensidade do campo magnético no entre ferro:
Indução magnética no núcleo:
Solução 7:
Da curva de magnetização para aço silício:
Força Magneto Motriz (Fmm):
Exercício 8
Considere a mesma estrutura, porém com uma bobina de 750 espiras, e uma
corrente de 6 A. Qual é o valor do fluxo no entreferro?
Solução
Substindo-se (5) em (1)
(1)
(2)
(3)
(4)
(5)
(6)
A equação (6) recebe o nome de reta
negativa de entreferro (Figura abaixo)
Fazendo-se
em (6):
Fazendo-se
em (6):
Do gráfico tiramos:
Portanto:
Exercício 9
Um núcleo toroidal de aço fundido apresenta uma seção transversal circular de 10
cm2. O comprimento médio do circuito magnético é 35 cm, com um gap de 1 mm.
Uma bobina enrolada com 200 espiras em torno do núcleo alimenta o circuito
magnético com uma corrente de 3 A. Determine o fluxo no entreferro.
Figura 11 - Circuito Magnético e circuito análogo do exemplo
Solução 9:
Raio do núcleo toroidal de aço fundido:
O circuito magnético é descrito por:
(1)
Raio efetivo do entreferro:
Como o circuito é de aço fundido,
, tem-se:
Área efetiva do entreferro:
(2)
Solução 9:
Na equação do circuito magnético (1) substituído por (2):
(3)
Fazendo
em (3):
Fazendo
em (3):
Do cruzamento da reta negativa de entreferro com a curva de magnetização
do material magnético do núcleo obtemos:
O fluxo no entreferro é: