T - Webnode

UESB-DCE-FÍSICA
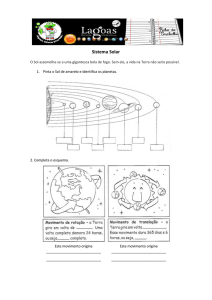
INTRODUÇÃO À ASTRONOMIA
PROF. SILVANIO B. DE OLIVEIRA
Parte 1
UNIDADE 1
1- ASTRONOMIA
1.1- De Galileu à Copérnico;
1.2- Esfera celeste e medidas estelares;
1.3- Sistema de coordenadas celeste;
1.4- Precessão;
1.5- Tempo;
1.6- Leis do movimento planetário;
1.7- Unidades de medidas astronômicas;
1.8- Gravitação hoje.
2- SISTEMA SOLAR: O SOL
2.1- A formação do Sistema Solar;
2.2- O Sol;
2.3- Fusão nuclear;
2.4- Neutrino, atmosfera, ventos, campo magnético, manchas e eclipse sola
3- SISTEMA SOLAR: OS PLANETAS
3.1- Definição e órbitas planetárias;
3.2- Propriedades planetárias;
3.3- Atmosfera planetária;
3.4- Os planetas do Sistema Solar;
3.5- Cometas.
UNIDADE 2
1- PLANETAS EXTRA-SOLAR
1.1 - Método de detecção de planetas;
1.2- Passagens planetárias;
1.3- Microlentes gravitacionais;
1.4- Astrometria;
1.5- Descoberta espacial;
2- OBSERVANDO O UNIVERSO
2.1- Instrumentos ópticos
3- PROPRIEDADES DAS ESTRELAS
3.1- Luminosidade, distância, movimento;
3.2- Escala de medidas absoluta;
3.3- Cor e temperatura da superfície;
3.4- Fotometria estelar;
3.5- Espectro estelar;
3.6- Massa e densidade estelar;
3.7- Tempo de vida de uma estrela.
4- EVOLUÇÃO ESTELAR
4.1- Massa estelar;
4.2- Estrelas variáveis;
4.3- Nebulosa planetária;
4.4- Anãs brancas;
4.5- Evolução de uma estrela tipo-Sol e em sistemas binários fechado
4.6- Estrelas massivas;
4.7- Supernova tipo II;
4.8- Estrelas de nêutron, buracos negro e pulsares.
UNIDADE 3
1- GALÁXIAS E ESTRUTURAS DE LARGA ESCAL DO UNIVERSO
1.1- A Via Láctea;
1.2- Outras galáxias;
1.3- O Universo;
2- COSMOLOGIA
2.1- O modelo do Big Bang;
2.2- Espectro das galáxias;
2.3- A expansão do Universo: Um problema com a
idade;
2.4- Microondas cósmicas;
2.5- Matéria e energia escura;
2.6- Vida inteligente no Universo.
INTRODUÇÃO
- A Astronomia é provavelmente uma das mais antigas de todas as
ciências.
- Nas civilizações antigas, o homem ainda continuava associar
divindades aos fenômenos naturais (astronômicos ou não).
- Os homens pré-histórico e antigo buscavam encontrar explicações
mitológicas para vários fenômenos celestes observados, entre os
quais: os dias, as noites, os eclipses da Lua e do Sol, as fases da
Lua, o deslocamento dos planetas entre as estrelas, os cometas e
as estrelas cadentes.
-Os babilônios1 foram um dos primeiros povos a registrar a
presença dos cinco planetas visíveis a olho nu (Mercúrio, Vênus,
Marte, Júpiter e Saturno), certamente sob a influência cultural dos
sumerianos.
1Povos
da Mesopotâmia, (região atual do Irã e Iraque), por volta do ano 3500 a.C., e os
sumerianos; ao longo do rio Nilo (atual Egito) em torno de 3100 a.C.
- Os deuses, os heróis e os animais desse povo eram associados
aos astros observados.
- Os babilônios buscavam entender as vontades dos deuses
observando os astros no céu, as quais se refletiam de algum modo
nos fatos terrestres.
- Conceberam as primeiras
representações de figuras
"desenhadas" pelas estrelas.
constelações, que eram apenas
de deuses, animais e objetos
- As constelações do Zodíaco são um exemplo.
- Assim, a Astrologia e a Astronomia nascem juntas, como uma
única forma de conhecimento.
PROVA DE GALILEU DA TEORIA COPERNIANA DO SISTEMA SOLAR
- Um dos primeiros triunfos da astronomia observacional foi obtido por
Galileu (Fig. 1.1) em suas observações de Vênus, que mostrou que o Sol,
não a Terra, era o centro do sistema solar.
-Dessa forma, ele mostrou que o modelo de
Copérnico estava correto.
-No modelo ptolomaico, os planetas movemse em ‘epicíclos’ circular, cujos centros
movem-se em torno da Terra em círculos
maiores chamados deferentes, como mostra
a Fig. 1.2.
-Neste modelo, Vênus localiza-se entre a
Terra e o Sol e portanto, sempre iluminado
lateralmente, mostrando fases crescentes e
mantendo o seu tamanho angular sem
alteração.
Fig. 1.1 - Imagem: Wikipeda
Commons
Fig. 1.2 - Pontos centrais dos epicíclos para Mercúrio e Vênus que se movem em torno da Terra com a
mesma velocidade angular do Sol. Fonte: Morison (2008)
- Em contraste, no modelo de Copérnico, Vênus orbita o Sol. Quando
próximo lateralmente, mostraria fases crescentes, enquanto que mais
afastado, mas ainda visível, mostraria fases quase cheia.
Fig. 1.3 – Desenho de Galileu de Vênus (topo)
comparado com a fotografia tirada a partir da
Terra. Fonte: Morison (2008)
ESFERA CELESTE E MAGNITUDES ESTELARES
- Olhando para o alto nos céus numa noite limpa, pode-se imaginar que
as estrelas estão localizadas por dentro de uma esfera, chamada esfera
celeste, cujo centro é o centro da Terra.
AS CONSTELAÇÕES
- É um grupo de estrelas no céu perto o suficiente para ter a aparência de
uma figura imaginária no céu.
- Uma constelação é um asterismo particular. No céu as estrelas de uma
constelação estão muito distantes umas das outras, mas aparecem
agrupadas em números.
- Constelações ocidentais são agrupados em duas partes, dividindo o céu
em mais ou menos os dois hemisférios terrestres, o céu do sul para o sul e
norte do céu ao norte.
CONSTELAÇÕES: ÁRIES, TOURO, GÊMEOS, CÂNCER, LEÃO, VIRGEM,
LA BALANÇA, ESCORPIÃO, SAGITÁRIO,
CAPRICÓRNIO, AQUÁRIOS E PEIXES.
MAGNITUDES ESTELARES.
- Os primeiros astrônomos registraram as posições das estrelas na esfera
celeste pelo seu brilho.
- O primeiro catálogo conhecido de estrelas foi feito pelo astrônomo grego
Hipparchos em aproximadamente 130-160 A.C.
- Em 150 D.C., Ptolomeu acrescentou outras estrelas neste catálogo
publicando um trabalho chamado de O Almagest, cujo catálogo enumerou
1028 estrelas.
- Hipparchos tinha agrupado as estrelas visíveis a olho nu em seis grupos
de magnitude. A mais brilhante denominado de 1a magnitude e a magnitude
mais fraca, de 6a.magnitude.
Quando medições exatas
do brilho estelar foram feitas antes do século XIX, em média, as estrelas de
uma dada magnitude foi aproximadamente 2.5 vezes mais brilhante do que
aquelas de magnitude mais fraca seguinte e que as estrelas de 1a
magnitude foram aproximadamente 100 vezes mais brilhantes do que as
estrelas de 6a magnitude.
- Tal diferença na magnitude, deve-se ao olho humano possuir um
logarítmico um tanto difícil na escala de brilho médio.
- Em 1854, Norman Pogson determina a escala de magnitude em um
quantitativo base de cinco diferentes magnitudes com brilho médio de precisão
100.
- Se definir o brilho médio de uma diferença de magnitude por R, logo uma
estrela de 5a magnitude será R vezes mais brilhante do que uma estrela de 6a
magnitude.
- De modo que uma estrela de 4a magnitude será RxR vezes mais brilhantes
do que uma estrela de 6a magnitude e uma estrela de 1a magnitude será
RxRxRxRxR mais brilhante do que uma estrela de 6a magnitude.
- Portanto, pela definição de Pogson, isto deve igualar a 100, de modo que,
R deve ser a 5a raiz de 100 que é aproximadamente 2,512.
- Logo, o brilho médio entre duas estrelas cuja magnitude aparente difere
por uma magnitude, é 2,512.
- Tendo definido a escala, foi necessário dar-lhe um ponto de referência. A
estrela variável Vega torna-se o ponto de referência com a sua magnitude
definida para ser o zero.
(Hoje, um método mais complexo é usado para definir o ponto de referência.)
MAGNITUDES APARENTES
- Deve-se notar que a magnitude observada de uma estrela não nos diz nada
do seu brilho intrínseco.
- Uma estrela que parece brilhante no céu pode ser uma estrela fraca que
resulta estar muito próximo do Sol ou uma estrela muito mais brilhante a uma
distância maior.
- Por conseguinte, essas magnitudes são denominadas magnitudes aparentes.
- Algumas estrelas e outros corpos celestes, como o Sol, Lua e planetas são
muito mais brilhante do que a estrela Vega, e assim, pode ter magnitudes
evidentes negativas.
- As magnitudes também podem ter partes fracionárias como, por exemplo,
Sirius que tem uma magnitude de -1,5.
- A Fig. 1.4 dá as magnitudes aparentes de uma variedade de corpos celestes
do mais brilhante, o Sol, ao planeta anão fraco, Plutão.
Fig. 1.4 – Alguns exemplos de magnitudes aparentes. Fonte: Morison (2008)
CÁLCULO DA MAGNITUDE
- Da definição logarítmica da escala de magnitude, duas fórmulas surgem.
- A primeira dá o brilho médio, R, de dois objetos cuja magnitude aparente se
diferencia por um valor conhecido m:
R = 2,512Δm
- A segunda dá a diferença de magnitude entre dois objetos cujo brilho
médio é conhecido.
- Toma-se os logaritmos à base 10 de ambos os lados da Eq. (1), isto é,
log10 R = log10(2,512)xΔm
log10 R = 0,4xΔm
Δm = log10 R/0,4
Δm = 2,5xlog10 R
(1)
- Como exemplo, usando valores da Fig 2.4, calcula-se quanto mais brilhante
o Sol é do que a Lua.
- A diferença em magnitudes é 26,7 – 12,6 = 14,1, portanto,
R = 2,51214,1  R = 436 800
- O Sol é ~ 440 000 vezes mais brilhantes do que a Lua cheia.
- Considere um segundo exemplo: uma estrela tem um brilho que é 10000
vezes menos do que a Vega (magnitude 0). Qual é a magnitude da estrela?
- Pela fórmula: Δm = 2,5 x log10(10 000)
= 2,5 x 4
= 10
SISTEMA DE COORDENADAS CELESTE
- O sistema de coordenadas celeste
é análogo ao sistema de
posicionamento geodésico utilizado
na superfície da Terra.
- O eixo de rotação da Terra é
prolongado até os pontos onde
intercepta a esfera celeste
imaginária.
- O ponto onde o eixo encontra a esfera diretamente acima do pólo Norte
é chamado o pólo Norte Celeste (zênite), e abaixo do pólo do Sul, é o pólo
Sul Celestial (nadir).
- Se o equador da Terra for estendido para fora ele cortará a esfera celeste
em dois – nos hemisférios do Norte e do Sul – formando o Equador
Celeste (ver Figura abaixo).
- A eclíptica é definida como uma circunferência imaginária correspondente
à trajetória aparente do Sol na esfera celeste, com iclinação de 23.5° em
relação ao Equador Celeste.
- A eclíptica cruza o Equador Celeste duas vezes ao ano: uma vez no
equinócio vernal, no dia 20 ou 21 de Março, e após de 6 meses, no
equinócio outonal, no dia 22 ou 23 de Setembro.
-Para definir as coordenadas de um astro no sistema equatorial,
primeiramente trace um grande semi-círculo na esfera celeste que passa
pelos pólos celestes e pelo astro, o que resultará no meridiano do astro.
-O ângulo medido ao longo desse meridiano, partindo do Equador celeste e
terminando no astro, é a primeira coordenada celeste denominada de
declinação (Dec).
- A declinação (altitude) é equivalente as latitudes terrestre, variando de 0o a
90o, no hemisfério norte celeste, e 0o a -90o no hemisfério sul celeste.
- Uma coordenada do sistema horizontal é o azimute ou ângulo azimutal,
o qual é medido ao longo do horizonte partindo do ponto cardeal Norte (0°),
no sentido horário (ou seja, de Norte para Leste), até o círculo vertical que
passa pelo astro.
- A segunda coordenada no sistema equatorial é um ângulo medido ao
longo do Equador celeste partindo de um dado ponto de referência até o
meridiano do astro. Note a semelhança com a definição de longitude
geográfica.
- Esse ângulo é chamado de ascensão reta, representado pela letra grega
alfa(α) ou, mais comumente, pela sigla em inglês, RA.
- Deve-se chamar a atenção para o fato de que a ascensão reta é medida
em unidades de tempo em vez de graus.
-Se dividirmos os 360° do círculo por 24, obtemos o valor 15. Assim, um
ângulo de 1 hora equivale a 15 graus.
- Suponha que a ascensão reta de uma estrela seja 3h 45min 18s.
-Para calcular esse ângulo em graus, deve-se primeiro calcular o total da
hora com suas frações, ou seja:
3 +45/60 + 18/3600 = 3.755h.
-Agora, para calcular esse valor em graus, multiplica-se por 15 e obtém-se
56.325°.
PRECESSÃO
- Se você localizar o ponto onde o Sol cruza o eclíptico no equinócio de
vernal em um mapa celeste (com posição: RA 0:00 h, Dec 0.0 °), você
perceberia que ele não está em Áries, mas em Peixes, constelação
adjacente.
- Este é o resultado da precessão do eixo de rotação da Terra.
- A taxa de precessão é lenta; uma rotação a cada ~26 000 anos, mas, o
seu efeito junto aos séculos deve modificar as posições de estrelas
medidas com o sistema de coordenada descrita anteriormente, que é fixa a
Terra.
- Consequentemente, um mapa celeste, só é válido em uma data
específica.
- Um resultado da precessão é que a Estrela Polar fica próximo ao pólo
Norte Celeste num determinado momento no ciclo de precessão (Figura
seguinte).
- Em ~12000 anos, a
estrela brilhante Vega
estará próximo do pólo
Celeste Norte.
- Isto significa que as
constelações atualmente
não observáveis do Reino
Unido ficarão visíveis
acima do horizonte Sul.
- Devido à precessão, as
estrelas
que
seriam
ocultas da visão nesta
região variará com o
tempo, e isto permite-nos
dar
uma
data,
aproximadamente 26002900 antes de Cristo,
quando as constelações
foram delineadas.
TEMPO
- A medida do tempo se baseia no movimento de rotação da Terra, que
provoca a rotação aparente da esfera celeste;
TEMPO SIDERAL
- É baseado no movimento aparente do Ponto Vernal (ou Ponto Áries);
- Intervalo de tempo decorrido entre duas passagens sucessivas do
Ponto Vernal pelo meridiano do lugar;
- Ponto Vernal – É um ponto do Equador, ocupado pelo Sol no equinócio
de primavera do Hemisfério Norte;
- Hora Sideral – É o ângulo horário do Ponto Vernal; pode ser medido a
partir de qualquer estrela;
- Ângulo Horário – É um ângulo medido sobre o Equador, com origem
no meridiano local e extremidade no meridiano do astro. Varia entre -12h
e +12h;
Dia Sideral – É o intervalo de tempo decorrido entre duas passagens
sucessivas do ponto Vernal pelo meridiano do lugar;
TEMPO SOLAR
-É baseado no movimento aparente do Sol.
- Hora Solar - é o ângulo horário do Sol. Uma hora corresponde ao
deslocamento angular de 15o.
- Dia Solar – é o intervalo de tempo decorrido entre duas passagens
sucessivas do Sol pelo meridiano do lugar.
-O dia solar é 3’56’’ mais longo que o dia sideral, devido ao movimento
de translação da Terra, aproximadamente 1o por dia.
- Como o Sol não é um ponto, e sim um disco, o ângulo horário do Sol
se refere ao centro do Sol, o qual é chamado de tempo solar verdadeiro.
-Como o Sol não tem um movimento uniforme ao longo do ano, tornase difícil medir o tempo usando o Sol como padrão. Daí surge a
definição de um Sol “médio” que define:
-Tempo Solar Médio – é o ângulo horário do centro do Sol médio.
-O Sol médio ou fictício, move-se ao longo do Equador celeste com 
constante, enquanto o Sol verdadeiro move-se ao longo da eclíptica
com  não-constante.
- Tempo Civil – usa como origem do dia o instante em que o sol médio
passa pelo meridiano inferior do lugar.
- A razão do tempo civil é não mudar a data durante as horas de maior
atividade da humanidade, ex: nos ramos financeiros, comerciais e
industriais, o que acarretaria problemas de ordem prática.
- Tempo Universal – é o tempo civil de Greenwich Mean Time (GMT)
com duração média do dia em 24 h.
FUSOS HORÁRIOS
- Cada fuso compreende 15o (=1 h). Fuso zero é aquele cujo meridiano
central passa por Greenwich.
- Os fusos variam de 0h a +12h para leste de Greenwich e de 0h a -12h
para oeste de Greenwich.
- Hora Legal – é a hora civil do meridiano central do fuso.
- Fusos no Brasil – o Brasil abrange quatro fusos:
- (-2h): arquipélago de Fernando de Noronha;
- (-3h): estados do litoral, Minas, Goiás, Tocantins e parte oriental do
Pará;
- (-4h): parte ocidental do Pará, parte oriental do Amazonas, Mato
Grosso do Norte e Mato Grosso do Sul;
- (-5h): parte ocidental do
-Amazonas e Acre.
- Através do uso do GMT, ocorrem diferenças nas medidas de tempo
durante o ano em relação ao Sol.
- Tais diferenças entre o GMT e o Tempo Solar Local no Greenwich é
chamada de ‘Equação do Tempo’ pelo Observatório Greenwich.
- A E.T. é definida como o ângulo
horário do Sol, menos o ângulo
horário do sol médio, expressa
por,
E = (ls-s) - (ls-lsm),
onde ls é a longitude eclíptica do
Sol e lsm é a longitude do sol
médio.
Figura 1.5 – ‘A equação do tempo’: a diferença entre o GMT e o Tempo Solar Local para o
observatório Greenwich
Tempo Universal
- O Tempo Médio Greenwich (GMT) foi formalmente substituído ao
Tempo Universal (UT) em 1928 (embora o título ainda não tenha
entrado no uso comum) mas foi essencialmente o mesmo como de
GREENWICH até 1967 quando a definição do segundo foi modificada.
- Antes disto, 1 s foi definido como 1/86 400 de um dia médio
determinado pela rotação da Terra.
- A taxa de rotação da Terra foi considerada de tempo fundamental
padrão.
- O problema com esta definição é que, devido às forças de maré da
Lua, a taxa de rotação da Terra está reduzindo gradualmente e, por
conseguinte, o comprimento do tempo definido pelo segundo
aumentava.
Em 1967, uma nova definição do segundo foi feita:
O segundo é a duração de 9 192 631 770 períodos da radiação
correspondente à transição entre os dois níveis do estado fundamental
do átomo de césio 133.
Um Padrão de Tempo Absoluto – Tempo Cósmico
- Em 1905, Albert Einstein, que então trabalhava no Escritório de Patentes de
Berna, publicou seu artigo da Teoria Especial da Relatividade.
-Um dos aspectos mais conhecidos desta teoria é que os relógios móveis
parecem correr lentamente comparando com um relógio fixo a um
observador – um fenômeno chamado dilação de tempo.
- Esta previsão foi provada pelos relógios atômicos precisos orbitando a
Terra, entre eles o sistema GPS usado para a navegação.
-Como o tempo relativo pode ser definido como padrão de tempo ao
observar a evolução do universo?
- A partir da definição do que poderia ser chamado o tempo cósmico como o
tempo medido por um relógio que é estacionário em relação ao universo.
- Como estes relógios se relacionaria com os da Terra?
- Sabemos que a Terra está movendo-se em volta do Sol, e que o Sol
está movendo em volta do centro da Galáxia Via Láctea ~ 220 milhão
de anos por volta.
- Pode-se medir a que velocidade o Sistema Solar move-se em relação
ao universo?
- Por simplicidade, suponha que o universo é composto de só um
comprimento de onda e que o Sistema Solar está movendo-se em
certa direção com respeito a esta radiação.
- O efeito Doppler alterará o comprimento de onda que observamos,
de modo que, olhando ao longo da direção na qual o Sistema Solar se
está movendo, o desvio será para o azul, parecendo ter um
comprimento de onda mais curto.
- De modo inverso, no sentido contrário, a radiação parecerá ser
desviada para o vermelho parecendo ter um comprimento de onda
mais longo.
- Das medições realizadas pelo CMB (“Cosmic Microwave Background”),
sabe-se que nosso sistema move-se em direção à constelação Leo a uma
velocidade de ~ 650 km/s (2 340 000 km/h ou 0.22% da velocidade da luz).
- Pode-se calcular como o tempo em um relógio atrasa em relação ao
universo – medir o tempo cósmico – vai se diferenciar dos nossos relógios.
- Para fazer isto, basta obter a fórmula que determina a dilação do tempo
como uma função da velocidade relativa.
- O relógio é feito refletindo um fóton para a frente e para trás entre um par
de espelhos perfeitos separados por uma distância, d, como visto na
Figura 1.6a.
- A 'marca' acontece a cada vez que o fóton reflete do espelho mais baixo e
portanto o fóton viajará uma distância 2a entre cada marca.
- O período de tempo fundamental, t1, será assim dado por :
T1 = 2d/c
Figura 1.6- (a) Um relógio de fóton fixo ao observador e (b) um relógio de fóton que se move em
uma velocidade v em relação ao observador.
- Suponha que observamos tal relógio movendo-se com velocidade v. (Fig.
1.6b.
- Para o observador, o fóton terá de viajar uma distância mais longa, l, entre
cada marca. Esta distância é dada por :
l = [(2d)2 + (vt2)2]1/2
- O intervalo de tempo entre cada marca, t2, será dado por :
t2 = l/c = [(4d2 + v2t2 2)/c2]1/2
- Elevando ambos os membros ao quadrado e multiplicando, obtém-se :
t22 c2 = 4d2 + v2 t22
- Relacionando t2 e t1 a v, e substituindo d2 = t12c2/4, obtém-se :
t22c2 = t12c2 + v2 t22
e
t22(c2 - v2) = t12c2
- Logo,
ou
t2/t1 = 1/[1 - (v2/c2)]1/2
t2/t1 = [c2/(c2 v2)]1/2
- Esta é a fórmula de dilatação de tempo, dado os intervalos de tempo médio
em função da velocidade relativa v.
- Portanto, como a nossa velocidade em relação ao universo é 650 km/s,
nesta equação obtém-se a proporção de 1.0000023.
- Este valor pequeno é uma aproximação muito boa, de modo que, os
nossos relógios podem ser usados para medir a escala de tempo do
universo.