Análise de Fadiga segundo o Método S-N Arquivo

Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Professores
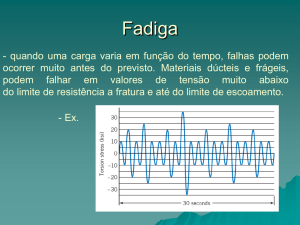
FADIGA DOS MATERIAIS
• Jorge Luiz Almeida Ferreira
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Aplicação
Projeto para Vida Segura
Filosofia utilizada quando a monitoração da trinca é difícil ou
antieconômica, e para componentes críticos quanto a segurança e
funcionamento,

Determinação da Resistência a Fadiga , e
 Previsão da iniciação de trincas de fadiga nas vidas longas, sob
tensões que são macroscopicamente elásticas
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Vantagens na Utilização do Método

Inúmeras Fontes de Informações Técnicas

Por trabalhar no regime linear elástico admite o uso do
princípio da superposição

Facilidades Computacionais

Robusto – Em geral prevê falha antes dela ocorrer
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Hipóteses Básicas

O material é modelado como contínuo, homogêneo, isotrópico, linear e
elástico,

A Máxima Tensão Equivalente do ponto analisado deve ser menor do que a
resistência ao escoamento material,

Baseia-se na correlação entre o início do trincamento de qualquer peça
com a vida de iniciação e propagação de trincas em corpos de prova
padronizados
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Origem do Estudo de Fadiga
1829 - Wilhelm August Julius Albert
Observou, estudou e publicou resultados de
testes realizados em correntes de ferro
submetidas a carregamentos cíclicos. Wilhelm
construiu
uma
máquina
que
carregava
repetidamente uma corrente. A sua descoberta
foi que a falha não era associada a sobrecargas
acidentais, mas sim dependente da carga e do
número de repetições dos ciclos de carga.
(1787 † – 1846 )
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Origem do Estudo de Fadiga
1830 - 1860 - Falhas em Eixos ferroviários
Sem motivo aparente, eixos ferroviários fraturavam após
apenas algumas centenas de quilômetros de serviço.
Embora projetados de acordo com critérios de
resistência estática, as fraturas ocorriam sob condições
de carregamento normal. Apesar de ensaios de tração
realizados no material antes da entrada em serviço
revelarem adequada ductilidade, a ruptura em serviço
não apresentava sinais de deformação plástica. Ainda,
estes mesmos ensaios realizados no material após a
fratura apresentavam as características de ductilidade
iniciais.
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Origem do Estudo de Fadiga
1860 - August Wöhler
Engenheiro alemão que estudou de forma sistemática o
comportamento de falha em eixos ferroviários. Dentre as
suas contribuições podem ser citadas:
- Ajudou a melhorar os procedimentos de testes de eixos
(aumentando a vida útil do eixo);
(1819 † – 1914 )
-
Desenvolveu o teste de fadiga rotativa de flexão;
-
Introduziu o conceito de limite de fadiga;
-
Iniciou o desenvolvimento de estratégias de projeto
contra fadiga e identificou o efeito das tensões
alternadas e médias e da presença de descontinuidades sobre o processo de falha.
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Origem do Estudo de Fadiga
Abordagem de Wöhler:
P
P
a
w
a
(1819 † – 1914 )
y
P
P
l
Mz
z
M=P∙l
z
y
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Origem do Estudo de Fadiga
Abordagem de Wöhler:
y
p
y, 
d
 Sin q 
2
d/2
y
q
Mz
xx (p)
z
z
(1819 † – 1914 )
x
  p 
y
z
Mz d
 Sin q 
Izz 2
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Origem do Estudo de Fadiga
Abordagem de Wöhler:
y
p
w
y, 
d
 Sin q 
2
d/2
y
q
Mz
z
z
q =?
q = w ∙t
(1819 † – 1914 )
xx (p)
x
y
I zz 
 d4
64
32  M z
  p 
 Sin w  t 
3
 d
z
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Origem do Estudo de Fadiga
Abordagem de Wöhler:
y
p
w
y, 
d
 Sin q 
2
(1819 † – 1914 )
d/2
q
Mz
z
z
y
 alt 
32  M z
 d3
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Origem do Estudo de Fadiga
Abordagem de Wöhler:
Uma das primeiras máquinas usadas foi
desenvolvida pelo Eng. August Wöhler
(22/06/1819 – 21/03/1914)
e serviu para
testar Corpos de Prova em balanço sob
flexão rotativa
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Origem do Estudo de Fadiga
1910 – O. H. Basquin
Utilizando dados obtidos por
Wöhler, desenvolveu e publicou
leis empíricas caracterizando a
relação
entre
a
tensão
alternada aplicada sobre um
componente mecânico e a sua
vida - curvas S-N (ou de
Wöhler). Ele mostrou uma
relação linear, em um gráfico
log-log, da tensão com o número
de ciclos até a falha.
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
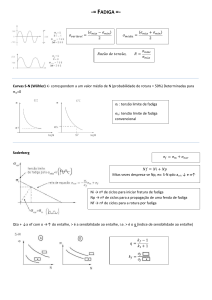
Filosofia do Método S-N
S-N Curve
Tensão (MPa)
Construção
de
relações
empíricas entre
a tensão
aplicada no ponto crítico de um
corpo de prova padronizado e o
tempo de vida necessário para
rompê-lo
S
Vida Finita
Limite de Resistência a Fadiga
Vida Infinita
104N 105 106 107 108
Log Vida (Ciclos)
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Análise da Resistência à Fadiga
Valer ressaltar, entretanto, que
a resistência do corpo de prova
depende
fortemente
dos
detalhes geométricos
S-N Curve
Tensão (MPa)
A resistência à fadiga do
material é uma propriedade
mecânica, medida por meio de
ensaios mecânicos realizados
sob condições de carregamento
simples.
S
Vida Finita
Limite de Resistência a Fadiga
Vida Infinita
104N 105 106 107 108
Log Vida (Ciclos)
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Evolução dos Ensaios S-N
15
10
5
Tensão
CPs de Fadiga São Testados em
Muitos Tipos de Máquinas
0
0
5
10
15
20
-5
Na máquina de ensaio proposta por R.
R. Moore, o efeito da presença de
esforços
cortante
é
anulado
utilizando o conceito de flexão em 4
pontos
-10
-15
Tempo
25
30
35
40
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Evolução dos Ensaios S-N
CPs de Fadiga São Testados em
Muitos Tipos de Máquinas
Nas máquinas de ensaio modernas o
controle de carga e facilidades de
intrumentação permitem a realização
de investigações mais completas e
complexas
além
obtenção
de
confiáveis
de
permitir
resultados
a
mais
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Evolução dos Ensaios S-N
CPs de Fadiga São Testados em
Muitos Tipos de Máquinas
controle de carga e facilidades de
intrumentação permitem a realização
de investigações mais completas e
complexas
além
obtenção
de
confiáveis
de
permitir
resultados
a
mais
30
20
Tensão
Nas máquinas de ensaio modernas o
40
10
0
-10
0
5
10
15
20
-20
-30
-40
Tempo
25
30
35
40
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Caracterização dos Esforços Geradores do Processo de Fadiga
Processo de Fadiga é Causado Primariamente
pela
Aplicação
de
Forma
Repetida
de
Esforços (Tensões e Deformações) sobre o(s)
Ponto(s)
Críticos
de
Estruturas.
Para
Caracterizar os Esforços são Utilizados os
Seguintes Parâmetros:
Tensão Alternada, a:
  min 

 a   max

2


Tensão Média, m:
  min 

 m   max

2


Gama de Tensão, :
    max   min
Razão de Carregamento, R:
R
 Min
 Max
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Análise da Curva de Resistência à Fadiga
S-N Curve
Conforme pode-se observar do
gráfico ao lado, a vida do corpo
Vida Finita
de prova, N, depende fortemente
do nível de tensão que é aplicado
Sf
na seção crítica do corpo de
Se
prova.
Limite de Resistência a Fadiga
Vida Infinita
103
104 N105 106 Ne
Log Vida (Ciclos)
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Análise da Curva de Resistência à Fadiga
Típicamente são adotadas as relações
Sf  AN
Log  N   A  b  S f
S-N Curve
para descrever a dependência entre a
resistência a fadiga, Sf, e a vida, N.
Tensão (MPa)
b
Vida Finita
Sf
Se
Limite de Validade: 103 < N < Ne
onde: Ne → Vida Infinita
Se → Limite de Resistência a Fadiga
Limite de Resistência a Fadiga
Vida Infinita
103
104 N105 106 Ne
Log Vida (Ciclos)
Atividade : Relatório sobre a
Norma ASTM 739
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Análise da Curva de Resistência à Fadiga
O Limite de Resistência a Fadiga
S-N Curve
foi observado por Wöhler quando
analisava
resultados
de
ensaios de fadiga em aço.
Para
aços,
infinita,
Ne,
considera-se
vidas
Sf
vida
entre
os
seguintes limites 106 e 107 ciclos
Outros materiais podem ou não apresentar
um limite de fadiga bem definido
Vida Finita
seus
Se
Limite de Resistência a Fadiga
Vida Infinita
103
104 N105 106 Ne
Log Vida (Ciclos)
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Equacionamento da Relação S-N
Conforme descrito anteriormente, a
S f  A  N b , 103 < N < Ne
 L og S f   L og  A   b  L og  N 
Assim,
com
base
em
dados
experimentais é possível, utilizandose técnicas de regressão linear
obter os valores de A e de b.
Log(S)
relação entre S e N é expressa por:
Log(103)
Log(N)
Log(Ne)
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Equacionamento da Relação S-N
6
Conforme descrito anteriormente, a
5
8
Tensão Alternada (x10 Pa)
relação entre S e N é expressa por:
S f  A  N b , 103 < N < Ne
 L og S f   L og  A   b  L og  N 
4
Lo te s
P o n tos E xp e rim e n ta is A m o stra A
P o n tos E xp e rim e n ta is A m o stra B
C u rva S -N - T en d ê n cia A m o stra A
Estudo com o Aço ASTM A743
CA6NM, mostrou que o seu Limite
de Resistência a Fadiga é 384 MPa
C u rva S -N - T en d ê n cia A m o stra B
L im ites do In terva lo d e C on fia nça
3
2
3
4
5
6
7 8 9
2
3
4
5
6
1E +5
7 8 9
2
1E + 6
V id a (N u m . d e C iclo s)
S  1406  N
0.094
3
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Equacionamento da Relação S-N
ausência
de
informações
experimentais confiáveis, ainda é
possível
estimar
a
curva
S-N
utilizando-se a seguinte receita:
N  10 3 , S f  S103
Log(S103)
Log(S)
Na
Log(Se)
 Log S103   Log  A   3  b
N  N e , S f  Se
 Log S e   Log  A   log  N e   b
Log(103)
Log(N)
Log(Ne)
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Equacionamento da Relação S-N
Resolvendo o Sistema:
 Se
log 
S 3
 10
b
A  10




Log(S103)
 Ne 
log  3 
 10 
log Se blog N e 
Log(Se)
Log(103)
Log(Ne)
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Equacionamento da Relação S-N
Para Aços admite-se que os valores
por meio das seguintes relações:
S103 = 0,9·Srt
Se = 0,5·Srt, Srt
≤ 1400MPa, ou
Log(S103)
Log(S)
de S103 e Se podem ser estimados
Log(Se)
= 700MPa, Srt >1400MPa
Ne =
106
Log(103)
Log(N)
Log(Ne)
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Equacionamento da Relação S-N
Para outros materiais o valor de Se pode ser estimado pelas relações
Ferros fundidos: Sf(106) = 0,4 . Srt
ligas de Alumínio: pode-se assumir um limite de resistência à fadiga em 5.108
ciclos, estimado por:
Sf(5.108) = 0,4.S Srt, Srt < 325 MPa ou
Sf(5.108) = 130MPa, Srt > 325MPa
ligas de Magnésio: Sf(108) = 0,35 . Srt
ligas de Cobre: Sf(108) = 0,25 a 0,50 . Srt
ligas de Níquel: Sf(108) = 0,35 a 0,5 . Srt
ligas de Titânio: Sf(106 a 107) = 0,45 a 0,65 .Srt
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Equacionamento da Relação S-N
Exemplo:
Estimar
Resistência
a
a
Fadiga
Curva
do
de
Aço Log(0,9·918)
ASTM A743 CA6NM
Amostra
Ensaio
A
1
1
2
B
Média
Desvio Padrão
Tensão de
Resistência [MPa]
890
919
917
918
16
Log(918/2)
3
6
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Equacionamento da Relação S-N
S  1406  N 0.094
Substituindo os valores teremos
Log(826)
 462.7 
log 

826


b
 106 
log  3 
 10 
 0,0839
Log(462,7)
A  10log200blog10   1475MPa
6
3
6
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Equacionamento da Relação S-N
metodologia
utilizada
consiste em acoplar à relação S-N
a equação de Basquin, ou seja:
Sf  AN b
Relação S-N
S f   ,f   2 N 
b
  Srt  50ksi
,
f
Eq. de Basquin
Log(S103)
Log(S)
Outra
Log(Se)
Log(103)
  Srt  345MPa
,
f
Log(N)
Log(Ne)
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Equacionamento da Relação S-N
Recorrendo a equação de Basquin,a
expoente b é realizada segundo a
seguinte expressão
 Se 
log  , 
 
f 

b
log 2  N e 
A    2
,
f
b
Log(S103)
Log(S)
estimativa da constante A e do
Log(Se)
Log(103)
Log(N)
Log(Ne)
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Equacionamento da Relação S-N
Exemplo: Estimar a Resistência a
Fadiga
do
Aço
ASTM
A743 Log(0,9·918)
CA6NM
Amostra
Ensaio
A
1
1
2
B
Média
Desvio Padrão
Tensão de
Resistência [MPa]
890
919
917
918
16
Log(918/2)
3
6
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Equacionamento da Relação S-N
1000
Sf = Srt + 345 = 1263 MPa
 462.6 
log 

1263 

b
 0.069
6
log 2 10

Tensão (MPa)
Srt = 918 MPa

A   ,f  2   1263  2 
b
 0.069
1o Método
100
1000
2o Método
10000
100000
1000000
Vida (N)
S  1406  N 0.094
 1192 MPa
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
A resistência à fadiga do material é medida em pequenos CPs padronizados com:
ò diâmetro específico, d  8mm,
ò sem entalhes ou tensões residuais,
ò acabamento polido,
ò testados em flexão rotativa de 4 pontos,
ò temperatura e atmosfera controladas
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Em Condições Reais de Uso :
ò diversos
fatores
influenciam
significativamente a vida à fadiga de
peças reais
ò os fatores que alteram as tensões
macroscópicas devem ser tratados
nas solicitações
ò mas quando a escala dimensional do
efeito do fator é pequena, é melhor
considerá-lo como modificador da
resistência à fadiga do material.
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Uma forma de estimar a resistência a fadiga de um componente
estrutural, Se, consiste no uso dos fatores de Marin:
S e  K a  K b  K c   S
'
e
Ka = Fator de Acabamento Superficial
Kb = Fator de Tamanho
Kc = Fator de Carregamento
Kd = Fator de Temperatura
Ke = Fator de Entalhe
Se, = Limite de Resistência a Fadiga do Material
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Fator de Acabamento Superficial - Ka
Procura caracterizar o efeito
sobre a resistência à fadiga do tipo
de acabamento que a superfície da
peça possui.
Para o Aço ASTM A743 CA6NM
Ka = 0,73 (Acabamento Usinado)
Ka = 0,35 (Corroído em Água Doce)
Ka = 0,24 (Corroído em Água Salgada)
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Fator de Acabamento Superficial em Função da Rugosidade Superficial - Ka
Ka
Fator de Acabamento Superficial em função da resistência à tração e da rugosidade
superficial média Ra medida em micropolegadas.
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Fator de Acabamento Superficial - Ka
Algumas Relações Empíricas
polida: ka = 1
retificada: ka = 1.58.Srt-0,085
laminada a frio ou usinado: ka = 4.51.Srt-0,265
laminada a quente: ka = 57.7.Srt-0.718
forjada: ka = 272 .Srt-0.995
[ Srt ] = MPa
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Projeto contra fadiga - Exemplo
Um eixo deve ser projetado
para que seja suportado por
mancais de rolos. A geometria
básica é mostrada na figura.
Aço AISI 1025, Lam. a Frio
Mechanical Properties
Metric
Hardness, Brinell
121
Tensile Strength, Ultimate
415 MPa
Tensile Strength, Yield
310 MPa
Elongation at Break
20 %
carga de 3,5 kN, a 100 mm do
Reduction of Area
45 %
mancal esquerdo.
Modulus of Elasticity
200 GPa
Poissons Ratio
0.29
Shear Modulus
80.0 GPa
Para um fator de projeto de
1,28, estime o diâmetro do eixo
de forma que ele suporte uma
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Projeto contra fadiga - Exemplo
R1  R2  2,1  1,4  3,5kN
Um eixo deve ser projetado
para que seja suportado por
mancais de rolos. A geometria
básica é mostrada na figura.
Para um fator de projeto de
Ra  3.5 
150
 2.1kN
250
Rb  3.5 
2.1kN
1,28, estime o diâmetro do eixo
de forma que ele suporte uma
carga de 3,5 kN, a 100 mm do
mancal esquerdo.
1.4 kN
Mmax = 210 kNxmm
100
 1.4kN
250
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Projeto contra fadiga - Exemplo
Identificação da Seção Critica:
R1  R2  2,1  1,4  3,5kN
y
Mz = 210 kNxmm
z
2.1kN
z
1.4 kN
y
Mmax = 210 kNxmm
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Projeto contra fadiga - Exemplo
Dimensionamento Estático:
  p Max 
y
w
d
y ,   Sin q 
2
p
d/2
FS
 32  M z  FS 
32  M z



S

d

y
3


 d
   Sy 
1
3
y
q
Mz
z
z
Sy
xx (p)
x
y
I zz 
 d4
64
32  M z
  p 
 Sin w  t 
3
 d
z
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Projeto contra fadiga - Exemplo
Dimensionamento Estático:
 32  210 10 N  mm1.28 

d  
  310MPa 


3
1
3
  p Max 
Sy
FS
 32  M z  FS 
32  M z

 Sy d  
3


 d
   Sy 
 20.671mm
d ≥ 20,67mm
1
3
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Projeto contra fadiga - Exemplo
Dimensionamento a Fadiga:
Se  K a   S
  p alt
'
e
Se

FS
 32  M z  FS 
32  M z



S

d

e
3
 d
   Se

Srt = 415 MPa
Ka = 0,8
Se  0.8  0.5  415  166MPa
 32  210 10 N  mm1.28 

d  
 166MPa 


3
d ≥ 25,45mm
1
3
 25.45mm
1
3
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Fator de Tamanho - Kb
Tração-Compressão
Flexão

Menor diâmetro

Maior diâmetro


O gradiente de tensão parece ser o responsável por ambos os efeitos
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Fator de Tamanho - Kb
No caso de flexão rotativa ou de torção de peças circulares:
Kb = (d /7,62)-0.1133
(2,0 < d < 80mm)
Outra receita é dada por:
d < 8 mm  Kb = 1
8 < d < 50mm  Kb = 0,90
50 < d < 80mm  Kb = 0,80
d > 80mm  Kb = 0,75 a 0,60
No caso de tração pura usar kb = 1
Este valor de kb = 1 em tração está associado ao fato do ser o gradiente de
tensões a causa do efeito de tamanho
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Projeto contra fadiga - Exemplo
Dimensionamento a Fadiga:
S e  K a  K b   S
  p alt
'
e
Se

FS


32  M z  FS

d  
   K a  K b  Se 
1
3
→ Kb
Se  0.8  0.9  0.5  415  149.9MPa
 32  210 10 N  mm1.28 

d  
 149.9MPa 


3
d ≥ 26.36mm
1
3
 26.36mm
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Projeto contra fadiga - Exemplo
Dimensionamento a Fadiga:
S e  K a  K b   S
Kb = (d /7,62)-0.1133
d
2.8867
  p alt
Se

FS
'
e
(2,0 < d < 80mm)
32  M z
 d 


S

0
.
8



e
3
 d
 7.62 
32  M z  7.62 0.1133

  0.8   0.5  415
 32  210 10 N  mm1.28  7.62
d  
 166MPa 

3
 0.1133



d ≥ 26,69mm
0.1133
1
3 0.1133
  S e'
 26.689mm
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Fator de Tamanho - Kb
Para peças não-circulares,
ou de carregamento por
flexão alternada, é comum
usar um deq para obter kb,
igualando as regiões das
peças
e
dos
CPs
com
(digamos) S > 0.95.Smax, por
exemplo:
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Fator de Carregamento - Kc
Carregamentos Torcionais : Kc = 0,577 (Von Mises)
No caso de carregamentos axiais puros usar
Kc = 0,92
quando
Srt < 1520MPa; ou
Kc = 1
se
Srt > 1520MPa
(uma provável causa para o uso desses valores sob condições de
carregamentos axiais puros está relacionada a falta de controle da
excentricidade nos testes axiais de tração-compressão, onde é muito
difícil alinhar as garras da máquina e eliminar os fletores indesejáveis)
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Fator de Temperatura - Kd
1.00
0.80
Kd
0.60
0.40
Limite de Resistencia a Tração [MPa]
S rt Tem p era tura d e Tra b a lho
Kd 
S rt Tem p era tura Am b iente
800
600
400
200
0.20
0
0.00
0
200
400
Temperatura [Celsius]
600
800
0
200
400
Temperatura [Celsius]
Aço Médio Carbono
600
800
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Fator de Entalhe - Ke
Entalhes são pontos preferenciais
de iniciação de trincas.
Tipicamente as tensões máximas
observadas nesses pontos podem
ser estimadas utilizando-se o
conceito de fator de concentração
de tensões, Kt, ou seja:
S M a x  K t  S No m
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Fator de Entalhe - Ke
•Entrento,
a
iniciação
de
uma
trinca
é
fortemente
dependente da presença de gradiente das tensões atuantes
no ponto crítico,
•
Como conseqüência, o efeito real dos entalhes pequenos em
fadiga é menor do que o valor teórico previsto por Kt
•
Assim, Para quantificar o efeito da presença do entalhe
sobre a fadiga introduz-se os conceitos do fator de redução
da resistência à fadiga Kf , e da sensibilidade ao entalhe, q.
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Fator de Redução de Resistência a Fadiga - Kf
O Fator de Redução da Resistência
relação:
Kf 
S n(C P Sem E nta lhe)
S n(C P C o m E nta lhe)
à Fadiga é definido pela seguinte
 S n(E nta lhe) 
S n(C P Sem E nta lhe)
Kf
Assim, de forma semelhante ao Fator de Concentração Teórico, o Fator de
Redução da Resistência à fadiga pode ser usado para estimar a tensão
máxima atuante no ponto mais solicitado do entalhe devido a aplicação de
uma tensão nominal de intensidade igual a Snom, ou seja:
S M a x  K f  S No m
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Relação entre Kt , Kf e o Material
O Fator de Concentração de Tensões, Kt, e o Fator de Redução da
Resistência à Fadiga, Kf, relacionam-se da seguinte Forma:
K f  1  q   K t  1
onde q representa a Sensibilidade do material a presença do entalhe
IMPORTANTE:
1  K f  Kt
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Fator de Sensibilidade a Presença de Entalhes - q
O Fator de Sensibilidade ao Entalhe, q, é um Parâmetro que Procura Quantificar o
Efeito do Material e das Dimensões do Entalhe sobre a Intensidade do Gradiente
de Tensões.
Sx
x
Tamanho
Tamanho
Médio
Médio dos
dos
Grãos
Grãos
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Fator de Sensibilidade a Presença de Entalhes - q
Relações Mais Usadas
Neuber (1958)
1
q
1
a  83.94  rt0.768
aN

a  353.2rt1.123
3

a  1.215  e191910
 rt
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Fator de Sensibilidade a Presença de Entalhes - q
Relações Mais Usadas
Neuber (1958)
1
q
1
aN

Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Fator de Sensibilidade a Presença de Entalhes - q
Relações Mais Usadas
Peterson (1959)
1
q
1 ap / 
Valores Típicos para a são os que seguem:
ap = 0,51mm (ligas de Al)
ap = 0,185·(700/Srt) mm (aços, Srt< 700MPa),
ou
ap = 0,025·(2000/Srt)1.9 mm (aços, Srt >700MPa)
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Fator de Sensibilidade a Presença de Entalhes - q
Relações Mais Usadas
Peterson (1959)
1
q
1 ap / 
Valores Típicos para a são os que seguem:
ap = 0,51mm (ligas de Al)
ap = 0,185·(700/Srt) mm (aços, Srt< 700MPa),
ou
ap = 0,025·(2000/Srt)1.9 mm (aços, Srt >700MPa)
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Fator de Entalhe, Ke
Limite de Resistência a Fadiga do Componente
1
Ke 
Kf
Cada Ponto Material
do Componente Terá a
Sua
Resistência
a
Fadiga
Se1
Se2
Se3
,
Se = Ka·Kb·Kc·Kd·Ke·Se
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Exemplo: Determinar a Resistência a Fadiga da Peça abaixo considerando
que a mesma é fabricado por usinagem em aço ASTM A743 CA6NM
400
Considere as seguintes condições:
200
- Carregamento Normal,
6R
200
- Carregamento Fletor
150
50
Espessura: 30 mm
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Exemplo: Determinar a Resistência a Fadiga da Peça abaixo considerando
que a mesma é fabricado por usinagem em aço ASTM A743 CA6NM
Propriedades do Material:
Srt = 918 MPa
S’e = 417 MPa (Flexão Rotativa)
Pontos Críticos
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Exemplo: Determinar a Resistência a Fadiga da Peça abaixo considerando
que a mesma é fabricada em aço ASTM A743 CA6NM
A – Determinação do Fator de acabamento, ka
Acabamento Usinado : ka = 4.51.Srt-0,265
O Dois Pontos Críticos possuem
Fator de Acabamento Iguais a 0,74
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Exemplo: Determinar a Resistência a Fadiga da Peça abaixo considerando
que a mesma é fabricada em aço ASTM A743 CA6NM
B – Determinação do Fator de Tamanho, kb
Carga de Tração : kb = 1
O Dois Pontos Críticos possuem
Fator de Tamanho Iguais a 1
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Exemplo: Determinar a Resistência a Fadiga da Peça abaixo considerando
que a mesma é fabricada em aço ASTM A743 CA6NM
B – Determinação do Fator de Tamanho, kb
Condição de Flexão:
Pescoço:
Kb = (de /7,62)-0.1133 = 0,8
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Exemplo: Determinar a Resistência a Fadiga da Peça abaixo considerando
que a mesma é fabricada em aço ASTM A743 CA6NM
B – Determinação do Fator de Tamanho, kb
Condição de Flexão:
Furo:
d e  0.808  t  h  d 
 0.808  30  200  50
 54,2mm
Kb = (de /7,62)-0.1133 = 0,801
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Exemplo: Determinar a Resistência a Fadiga da Peça abaixo considerando
que a mesma é fabricada em aço ASTM A743 CA6NM
C – Determinação do Fator de Carregamento, kc
Carga de Tração : kc = 0,92 (Srt < 1520 MPa)
O Dois Pontos Críticos possuem
Fator de Carregamento Iguais a 0,92
Carga de Flexão : kc = 1
O Dois Pontos Críticos possuem
Fator de Carregamento Iguais a 1
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Exemplo: Determinar a Resistência a Fadiga da Peça abaixo considerando
que a mesma é fabricada em aço ASTM A743 CA6NM
D – Determinação do Fator de Temperatura, kd
Temperatura Ambiente : kd = 1
O Dois Pontos Críticos possuem
Fator de Carregamento Iguais a 1
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Exemplo: Determinar a Resistência a Fadiga da Peça abaixo considerando
Tração
que a mesma é fabricada em aço ASTM A743 CA6NM
E.1.1 – Fator de Concentração de Tensões, Kt, Pescoço
Solução Gráfica - Peterson
Kt ≈ 2,8
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Exemplo: Determinar a Resistência a Fadiga da Peça abaixo considerando
que a mesma é fabricada em aço ASTM A743 CA6NM
E – Determinação do Fator de Entalhe, ke
E.1 – Fator Teórico de Concentração de Tensões, Kt
Pescoço: Kt ≈ 2,67
Forma de Obtenção: Elementos Finitos
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Exemplo: Determinar a Resistência a Fadiga da Peça abaixo considerando
que a mesma é fabricada em aço ASTM A743 CA6NM
Tração
E.1.1 – Fator de Concentração de Tensões, Kt, Furo
Solução Gráfica - Peterson
Kt ≈ 2,42
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Exemplo: Determinar a Resistência a Fadiga da Peça abaixo considerando
que a mesma é fabricada em aço ASTM A743 CA6NM
E – Determinação do Fator de Entalhe, ke
E.1 – Fator Teórico de Concentração de Tensões, Kt
Furo : Kt ≈ 2,62
A2
Motivo da diferença entre E.F e Peterson:
A1
Efeito de Borda
Borda muito Próxima do Furo
Forma de Obtenção: Elementos Finitos
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Exemplo: Determinar a Resistência a Fadiga da Peça abaixo considerando
que a mesma é fabricada em aço ASTM A743 CA6NM
E – Determinação do Fator de Entalhe, ke
E.1 – Fator Teórico de Concentração de Tensões, Kt
Solução Placa com Furo considerando que
as bordas laterais estão distantes do Furo
A2
Kt = 2,27
Bordas muito Distantes do Furo
Forma de Obtenção: Elementos Finitos
A1
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Exemplo: Determinar a Resistência a Fadiga da Peça abaixo considerando
que a mesma é fabricada em aço ASTM A743 CA6NM
E – Determinação do Fator de Entalhe, ke
E.1 – Fator Teórico de Concentração de Tensões, Kt
Tração
Fonte Metodologia: Peterson
Fonte Metodologia: MEF
Furo: Kt ≈ 2,42
Furo: Kt ≈ 2,62
Pescoço: Kt ≈ 2,8
Pescoço: Kt ≈ 2,67
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Exemplo: Determinar a Resistência a Fadiga da Peça abaixo considerando
que a mesma é fabricada em aço ASTM A743 CA6NM
E – Determinação do Fator de Entalhe, ke
E.1 – Fator de Sensibilidade ao Entalhe, q
1
Peterson (1959) q 
1 ap / 
ap = 0,185·(700/Srt) mm (aços, Srt< 700MPa), ou
ap = 0,025·(2000/Srt)1.9 mm (aços, Srt >700MPa)
ap = 0,1098
Furo = 25 mm
Pesc = 6 mm
qFuro = 0,996
qPesc = 0,982
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Exemplo: Determinar a Resistência a Fadiga da Peça abaixo considerando
que a mesma é fabricada em aço ASTM A743 CA6NM
E – Determinação do Fator de Entalhe, ke
E.2 – Fator de Redução de Resistencia a Fadiga, Kf
K f  1  q   K t  1
KtFuro = 2,62; qFuro = 0,996
KfFuro = 2,613
KtPesc = 2,8;
KfPesc = 2,768
qPesc = 0,982
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Exemplo: Determinar a Resistência a Fadiga da Peça abaixo considerando
que a mesma é fabricada em aço ASTM A743 CA6NM
1
S e  0.74 1 0.92 
 417  108.6
2.613
Resistência a Fadiga sob Condição
de Carregamento Normal
1
S e  0.74 1 0.92 
 417  102.6
2.768
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Exemplo: Determinar a Resistência a Fadiga da Peça abaixo considerando
que a mesma é fabricada em aço ASTM A743 CA6NM
Flexão
E.1.1 – Fator de Concentração de Tensões, Kt, Pescoço
Solução Gráfica - Peterson
Kt ≈ 2,3
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Exemplo: Determinar a Resistência a Fadiga da Peça abaixo considerando
que a mesma é fabricada em aço ASTM A743 CA6NM
E.1.1 – Fator de Concentração de Tensões, Kt, Pescoço
Kt ≈ 2,0
Forma de Obtenção: Elementos Finitos
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Exemplo: Determinar a Resistência a Fadiga da Peça abaixo considerando
que a mesma é fabricada em aço ASTM A743 CA6NM
E.1.1 – Fator de Concentração de Tensões, Kt, Pescoço
Kt ≈ 2,0
Forma de Obtenção: Elementos Finitos
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Exemplo: Determinar a Resistência a Fadiga da Peça abaixo considerando
que a mesma é fabricada em aço ASTM A743 CA6NM
E.1.2 – Fator de Concentração de Tensões, Kt, Furo
Solução Gráfica - Roark
(1) – Kt(A) = 2
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Exemplo: Determinar a Resistência a Fadiga da Peça abaixo considerando
que a mesma é fabricada em aço ASTM A743 CA6NM
Carga Admissível de Tração sob Condição de Fadiga
nom ≡Se  F  S  F  105.7 MPa 150mm  30mm
H t
F  475.6kN
e
nom ≡Se
F
 Se
H t
 F  107.3MPa  200  25mm  30mm  563.3kN
F  563.3kN

Fadm ≤ 475,6kN
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Curva de Resistência a Fadiga Corrigida em Função dos Fatores de Marin
Sa
0.9S
0,9rtSrt
,
Sn
Se
,
Sn = Ka·Kb·Kc·Kd·Ke·Sn
Sn
1E+3
1E+4
Ne
1E+5
Número de Ciclos
1E+6
1E+7
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Curva de Resistência a Fadiga Corrigida em Função dos Fatores de Marin
Modelo 1 – Modelo de Shigley (Shigley, 1989 e Dowling, 1999)
Sa
0.9S
0,9rt
Srt
,
Sn
Se
,
Sn
1E+3
Sn = Ka·Kb·Kc·Kd·Ke·Sn
Ne
Número de Ciclos
N∞
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Curva de Resistência a Fadiga Corrigida em Função dos Fatores de Marin
Modelo 2 – Modelo de Heywood (Juvinall, 1991 e Yung-Li Lee, 2005)
Sa
,
0,9 Srt
Flexão e Torsão
Sn
Se
,
Sn
Sn = Ka·Kb·Kc·Kd·Ke·Sn
Carga Axial:
1E+3
Ne
Número de Ciclos
N∞
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Curva de Resistência a Fadiga Corrigida em Função dos Fatores de Marin
Modelo 3 – Modelo de Collins (Yung-Li Lee, 2005)
Sa
,
0,9 Srt
Sn
Se
,
Sn
Sn = Ka·Kb·Kc·Kd·Ke·Sn
= Const de Basquim
Aços
 ,f  Srt  345MPa
1
Ne
Número de Ciclos
N∞
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Curva de Resistência a Fadiga Corrigida em Função dos Fatores de Marin
Modelo 2 – Modelo de Heywood Modificado (Shigley, 2004 e Yung-Li Lee, 2005)
Sa
,
0,9 Srt
Flexão e Torsão
Sn
Se
,
Sn
Sn = Ka·Kb·Kc·Kd·Ke·Sn
Carga Axial:
1E+3
1E+4
Ne
1E+5
Número de Ciclos
1E+6
1E+7
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Efeito da Presença de Tensão Média
1000
Experimental Data
9
R = -1
8
Tensão normal de
Tração aumenta
R=0
7
R = 1/3
6
R = 2/3
Stress, S
Trend Line
5
Sa MPa
4
3
2
Cycles (Log N)
A vida em fadiga é fortemente influenciada
pela presença de tensões normais médias
100
1E+5
2
3
4
Life [Number of Cycle]
5
6
7
8
9 1E+6
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Efeito da Presença de Tensão Média – Diagrama de Haig
Vida Especificada N
1000
Experimental Data
9
R = -1
8
R=0
7
R = 1/3
6
R = 2/3
Trend Line
5
Sa MPa
4
3
2
100
1E+5
2
3
4
Life [Number of Cycle]
5
6
7
8
9 1E+6
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Efeito da Presença de Tensão Média – Modelos de Previsão
Melhor Ajuste para os
Pontos Experimentais ?
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Efeito da Presença de Tensão Média – Equação de Goodman (1899)
Vida = N
Sa = 0
Sm = 0
Sa (Tensão Alternada)
Se(N)
 Sm 
S a  Se N   1  
 S rt 
S a  Tensão Alternada
S m  Tensão Normal Média
S e ( N )  Limite de fadiga para S m  0
S rt  Limite de Resistênci a a Tração
Sm (Tensão Média)
Srt
Justificativas Apresentadas por Goodman:
- Fácil
- Segura
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Efeito da Presença de Tensão Média – Equação de Gerber (1874)
  S 2 
S a  Se N   1   m  
  S rt  


Vida = N
Sa (Tensão Alternada)
Se(N)
S m  Tensão Normal Média
S e ( N )  Limite de fadiga para S m  0
S rt  Limite de Resistênci a a Tração
Sm = 0
Sa = 0
S a  Tensão Alternada
Sm (Tensão Média)
Srt
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Efeito da Presença de Tensão Média – Modelos mais recentes
Baseando-se em observações empíricas verifica-se que carregamentos com
amplitudes de tensão relativamente baixas e tensões médias relativamente
elevadas induzem o aparecimento da falha antes do previsto pelos modelos
anteriores
Ensaios com níveis de tensão
próximos a
condição de
escoamento do material não são
triviais e geralmente se faz sob
controle de deslocamento.
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Efeito da Presença de Tensão Média – Smith-Watson-Topper (1970)
S ar  S a R  1  A  N b
1 R
 m   a 
 S ar
2
 a  Limite de Fadiga na presença de  m
 m  Tensão Normal Média
S ar  Limite de Fadiga para  m  0
R  Razão de Tensões
Sa = 0
Sm = 0
2
a 
 S ar
1 R
Se(N)
Vida = N
Sa (Tensão Alternada)
 m   a    a  S ar2
Sm (Tensão Média)
Srt
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Efeito da Presença de Tensão Média – Walker (1970)
 m   a 
1

  a  Sar
1
 2 
 a 
  S ar
1 R 

1 R 
 m   a   
  S ar
 2 
 a  Limite de Fadiga na presença de  m
 m  Tensão Normal Média
S ar  Limite de Fadiga para  m  0
R  Razão de Tensões
  Parâmetro do Material
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Efeito da Presença de Tensão Média – Walker - Comportamento Típico
1.0
a
Sar
0.8
 = 0,7
 m   a 
1
0.6
Gerber (Reference Model)
0.4
 = 0,5 (S-W-T)
0.2
 = 0,1
0.0
0.0
0.2
0.4
0.6
 = 0,3
0.8
1.0
1.2
m
S rt
  a  Sar
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Efeito da Presença de Tensão Média – Kwofie (2001)
a  S
'
f R1
e
 a  S ar  e
 m
 
S rt

 m
 

Srt








 N 
b
 a  Limite de Fadiga na presença d e  m
 m  Tensão Normal Média
S 'f R1  Cons tan te de Basquin
bR  1  Expoente de Basquin
  Parâmetro do Material
N  Numero de Ciclos
S ar  Limite de Fadiga para  m  0
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Efeito da Presença de Tensão Média – Kwofie - Comportamento Típico
1.0
a
 = 0,1
Sar
0.8
 = 0,3
= 0,5
0.6
Gerber (Reference Model)
0.4
 a  S ar  e
 = 0,7
0.2
= 2
0.0
0.0
0.2
0.4
0.6
0.8
1.0
1.2
m
 m
 

Srt





Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Efeito da Presença de Tensão Média – Particularização do Modelo de Kwofie
Hipóteses
=1
Equação Resultante
a
S ar
=1
a
Sy controla o efeito da tensão média
S ar
  
  f  m   m
 Srt  Srt
a
  
  f  m'   m'
S  S
f
 f 
a
S ar
S ar


m
S rt
m
Sy
Modelo
1
Goodman, Eq.
(2.4)
1
Soderberg, Eq.
(2.6)
2

 m
S
 y

 1



  m'
S
 f

 1


Gerber, Eq. (2.3)
2
Morrow, Eq. (2.7)
1
  f R, S rt ,  m   
S rt
1 R 
 Ln

2  m
 2 
1 R  2
 a  S ar  

 2 
  f R, S rt ,  m   
S rt
1 R 
 Ln

  m
 2 
 a  S ar  
1 R 

 2 
Smith-WatsonTopper, Eq. (2.8)

Walker, Eq. (2.9)
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Efeito da Presença de Tensão Média – Análise do Aço ASTM A743 CA6NM
1000
9
Goodman
8
7
Modelo de Kwofie
 a  1406  e
5
4
 N 
Sar [MPa]
 

 1 .453 m 
918 

Confidence Interval Limits - Kwofie Eq.
6
Gerber
3
R = -1
R=0
 0 .094
2
R = 1/3
R = 2/3
Trend Line - Kwofie Eq.
Basquin Eq. Based on Experimental Data
1000
Confidence Interval Limits - Basquin Eq.
Modelo de Walker
100
1.0E+3
1.0E+4
1.0E+5
1.0E+6
9
8
1.0E+7
Number of Cycle (N)
7
6
Confidence Interval Limits - Walker Eq.
5
 2 
 a 

1 R 
Sar [MPa]
4
1 0 .407
 1406  N
 0 .094
3
R = -1
R=0
2
R = 1/3
R = 2/3
Trend Line - Walker Eq.
Basquin Eq. Based on Experimental Data
Confidence Interval Limits - Basquin Eq.
100
1.0E+3
1.0E+4
1.0E+5
Number of Cycle (N)
1.0E+6
1.0E+7
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Verificação da Condição de Falha
Tensão Alternada, Sa
Syt
Sy
Como Representar a Condição de
Escoamento nesse Diagrama ??
Sar
Sa
smax = sa + sm = Syt
sa = sm - Syt
Sm
Syt
Srt Tensão Média, S
m
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Verificação da Condição de Falha
1
Syt
Tensão Alternada, Sa
Sm 
Se
S yt
Não Falha por Escoamento
nem por Fadiga
Se
1
1

S e S rt
Não Falha por Fadiga, mas
Falha por Escoamento
Não Falha por Escoamento,
mas Falha por Fadiga
Falha por Escoamento e
por Fadiga
Sa
Sm
Syt
Srt
Tensão Média, Sm
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Verificação da Condição de Falha
Sar
O ponto mais solicitado de um
componente mecânico está sujeito ao
par (Sm, Sa).
Diagrama construído para
uma Vida de N ciclos
Se(N)
Tensão Alternada, Sa
O componente falhará por fadiga ?
Qual o tempo de vida até a falha ?
Sa
S ar 
 Sm 
1  
 S rt 
(Sm, Sa)
Srt
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Verificação da Condição de Falha
Diagrama construído para
uma Vida de N ciclos
Se(N)
Tensão Alternada, Sa
Sar
S = A Nb
(Sm, Sa)
N
Srt
S 
N   ar 
 A 
1
b
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Efeito da Presença de Tensão Média – Exemplo de Aplicação
Uma liga de aço de alta resistência tem um limite de fadiga
de 500 MPa e um limite de resistência de 1000 MPa.
O material falhará se a tensão cíclica variar entre 0 e 400
MPa ?
Um processo de soldagem introduziu tensões residuais de
tração da ordem de 500 MPa. Que efeito isto trará ?
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Projeto Estrutural usando o Método Tensão-Vida
o método SN correlaciona o tempo de iniciação
SMax
=Kf·SNom.
de uma trinca de fadiga nos pontos críticos
(geralmente as raizes de entalhes) de qualquer
peça com a vida de pequenos CPs, que tenham a
mesma resistência daquele ponto e que sejam
submetidos à mesma história de tensões s em
Sy
P
serviço.
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Projeto Estrutural usando o Método Tensão-Vida
Rotina Básica de projeto :
SMax =
Kf·SNom.
1: avaliar a resistência à fadiga do ponto
crítico da peça (incluindo o efeito dos detalhes
que afetam a resistência à fadiga)
2: calcular a história de tensões S(t) nele
induzida pelo carregamento real
Sy
P
3: quantificar o dano acumulado pelos diversos
eventos do carregamento
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Técnicas para Minimizar o efeito dos Concentradores de Tensão sobre a
Fadiga
Suavizar o Fluxo dos Esforços, retirando material se
necessário
Projeto Eficiente
Projeto Pobre
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Técnicas para Minimizar o efeito dos Concentradores de Tensão sobre a
Fadiga
Reverter o fluxo das linhas de força diminui o Kt
Projeto Eficiente
Projeto Pobre
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Técnicas para Minimizar o efeito dos Concentradores de Tensão sobre a
Fadiga
No Parafuso, as Linhas de Força são Melhor Distribuídas se a Fêmea
da União Roscada também trabalhar à tração.
Projeto Pobre
Projeto Pobre
Projeto Eficiente
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Técnicas para Minimizar o efeito dos Concentradores de Tensão sobre a
Fadiga
Cantos Vivos têm Kt Grande e Devem ser Evitados
Projeto
Pobre
Projeto
Eficiente
Projeto
Pobre
Projeto
Eficiente
Projeto
Pobre
Projeto
Eficiente
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Técnicas para Minimizar o efeito dos Concentradores de Tensão sobre a
Fadiga
Projetos Eficientes
Retirar material para
diminuir a
engaste
rigidez do
gera
um
Kt
menor e aumenta a sua
resistência final
Análise de Fadiga Segundo o Método Tensão – Vida (S-N) – Módulo 2.1
Resistência à Fadiga de Componentes Estruturais
Técnicas para Minimizar o efeito dos Concentradores de Tensão sobre a
Fadiga
Outros
Projetos
Eficientes