Física 1
Fundamentos de Mecânica
Movimento Retilíneo
Prof. Alexandre W. Arins
Movimento em uma dimensão
•
•
•
•
•
•
•
•
Movimento
Posição e deslocamento
Velocidade média e velocidade escalar média
Velocidade instantânea e velocidade escalar
Movimento retilíneo uniforme (MRU)
Aceleração
Movimento retilíneo uniformemente variado (MRUV)
Queda livre
• A Mecânica estuda o movimento e as suas
causas.
• A sua descrição é feita pela Cinemática.
• As suas causas são descritas pela Dinâmica.
• Iniciamos com o movimento em 1- D.
Movimento
Dependendo do referencial adotado podemos considerar
que tudo no planeta Terra está em movimento.
Mesmo as coisas aparentemente imóveis, como uma
rodovia, estão em movimento, devido à rotação da Terra
em torno do seu eixo, ao movimento orbital da Terra em
torno do Sol, ao movimento orbital do Sol em relação ao
centro da Via-Láctea e ao deslocamento da galáxia em
relação a outras galáxias.
Iremos considerar inicialmente que os corpos em
movimento são partículas (um objeto puntiforme), ou
corpos que se movem como uma partícula (todos os
pontos se deslocam na mesma direção e com a mesma
velocidade). Uma criança deslizando para baixo num
escorregador reto de playground pode ser tratado como
uma partícula.
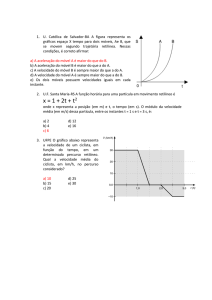
Posição e Deslocamento
Localizar um objeto significa determinar sua
posição relativa a um ponto de referência, em
geral, a origem (ou ponto zero) de um eixo,
como o eixo x na figura abaixo.
O sentido positivo do eixo é crescente na
escala numérica, ou seja, para a direita, na
figura. O sentido negativo é oposto.
Por exemplo, uma partícula pode estar localizada em x = 3 m,
significando que está a 3 m da origem, no sentido positivo.
Se fosse em x = - 3 m, estaria, igualmente, afastada da
origem, mas no sentido oposto.
A variação de uma posição x1 para outra posição x2, chamase deslocamento Dx, onde
Dx x2 x1
• O deslocamento é um exemplo de grandeza vetorial,
porque possui módulo, direção e sentido.
• Importante: Não confundir deslocamento, que é uma
grandeza vetorial, e representa a diferença entre a
posição inicial e a final do móvel, com distância
percorrida, que é uma grandeza escalar, e representa o
percurso total entre o início e o fim do movimento, sem
levar em conta a direção ou o sentido.
Velocidade Média e
Velocidade Escalar Média
Quando uma particular se move da posição x1 para x2,
num intervalo de tempo Dt = t2 – t1, sua velocidade
média é dada por:
Dx
v
Dt
O sinal algébrico indica o sentido do movimento.
A velocidade média depende da distância entre o ponto inicial e final
do movimento, e não da distância total percorrida pela partícula.
Velocidade Média
Num gráfico de x versus t, a velocidade média, em um
intervalo Dt, é a inclinação da reta que une os pontos
correspondentes ao início e ao fim do intervalo
considerado.
A velocidade escalar média de uma partícula depende
da distância total percorrida no intervalo de tempo Dt e
pode ser expressa por
distância percorrida
v
Dt
Velocidade Instantânea e
Velocidade Escalar
Se Dt tende a zero, então Dx também tenderá a zero;
entretanto, sua razão, que é v tenderá a um valor limite
v, que é a velocidade instantânea (ou simplesmente
velocidade) da partícula no instante considerado, ou
Dx dx
v lim
Dt 0 Dt
dt
A velocidade instantânea (num determinado instante) pode
ser representada pela inclinação (naquele ponto) da curva
de x versus t.
A velocidade pode ser calculada derivando-se a função x(t).
O módulo da velocidade instantânea é a velocidade escalar.
Movimento Retilíneo Uniforme (MRU)
Não é difícil encontrarmos corpos que se movimentam
com velocidade escalar constante. Por exemplo, numa
roda-gigante em movimento, todas as cadeiras
executam um movimento semelhante ao da extremidade
do ponteiro do relógio. Ou seja, nos dois casos a
velocidade dos móveis é constante. O mesmo acontece
com um automóvel cuja indicação do velocímetro é
sempre a mesma para certo intervalo de tempo.
Um movimento que apresenta a velocidade escalar constante
num intervalo de tempo é chamado de movimento uniforme (MU).
Em todo movimento uniforme, a velocidade escalar instantânea
coincide com a velocidade escalar média, ambas são constantes
e diferentes de zero.
Para determinar a função horária do espaço para o movimento uniforme
vamos estabelecer que o movimento passou a ser observado a partir do
instante do acionamento de um cronômetro (t0 = 0) e o móvel já possui
velocidade constante e diferente de zero. Nesse instante, o espaço do
móvel recebe o nome de espaço inicial (x0).
No instante t > t0, o espaço vale x. Assim:
Dx x x0 x x0
v
Dt
t t0
t 0
x x0 vt
Gráficos do MRU
x x0 vt
Aceleração
Quando a velocidade de uma partícula varia, dizemos
que ela está sob uma aceleração (ou está acelerada).
A aceleração média em um intervalo de tempo Dt é
Δv v2 v1
am
Δt t 2 t1
A unidade no SI da aceleração é
metro por segundo por segundo: m/(s.s) ou m/s2.
Outras unidades podem aparecer, mas sempre aparecerão
na forma de distância/tempo2.
A aceleração possui módulo, direção e sentido e por isso
é uma grandeza vetorial.
O sinal algébrico representa o sentido num dado eixo,
da mesma forma que para o deslocamento e a
velocidade.
Nosso corpo reage às acelerações (é um acelerômetro),
mas não às velocidades (não é um velocímetro). Quando
estamos viajando num carro a 100 km/h, ou num avião a
1000 km/h, não temos sensação corporal de estarmos
em movimento. Mas, se o carro ou o avião variar a
velocidade bruscamente, somos capazes de sentir tal
variação. Num parque de diversões, as maiores
sensações são causadas pelos brinquedos que nos
submetem a variações súbitas de velocidade.
Movimento Retilíneo Uniformemente
Variado (MRUV)
Em muitos tipos de movimento, a aceleração é constante, ou
aproximadamente constante.
Por exemplo, podemos acelerar um carro de forma
aproximadamente constante quando um sinal de trânsito passa
de vermelho para verde. Se depois tivermos que frear o carro
até parar, a desaceleração, durante a freada, também pode ser
considerada aproximadamente constante.
Quando a aceleração de uma partícula permanece
constante em um determinado intervalo de tempo dizemos
que esse movimento é uniformemente variado.
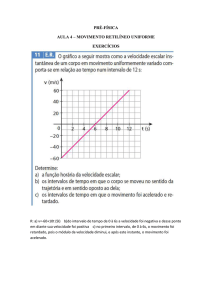
Gráfico da velocidade em função do tempo
(v x t)
v v0 at
Gráfico da aceleração em função do tempo
(a x t)
Aceleração = constante
Gráfico do espaço em função do tempo
2
at
x x 0 v0 t
2
Equação de Torricelli
Galileu Galilei
Criador do Método Experimental
Suas ideias e hipóteses eram
sempre observadas, testadas e
experimentadas.
Resistência do ar
É uma força de atrito que o ar exerce sobre o corpo
dificultando a realização do movimento.
Esta força tem sentido oposto ao da queda do corpo.
Quanto maior a superfície em contato com o ar,
maior será a resistência.
Simulando a queda dos corpos
Ar
Vácuo
Queda livre de um elefante e de uma pena
No ar
No vácuo
Movimento de descida
é acelerado
Movimento de subida
é desacelerado
Ti=0s
T=3s
Vi= 0m/s
V= 0m/s
T=1s
V= 10m/s
T=2s
V= 20m/s
T=3s
V= 30m/s
Nos movimentos
observados a
resistência do ar
é desprezada.
Aceleração que
atua na bola é a
da gravidade
(~10m/s2).
T=2s
V= 10m/s
T=1s
V= 20m/s
Ti=0s
Vi= 30m/s
Queda livre
• Podemos particularizar o conjunto de equações
anteriormente deduzidas para o MRUV, para a situação do
movimento de queda livre.
• Para todos os efeitos práticos, um corpo que cai próximo à
Terra, se comporta como se a superfície fosse plana e a
aceleração da gravidade g é considerada constante.
Iremos usar valor de g = 9,8 m/s2, e considerar o eixo y
apontando para cima da superfície da Terra.
• O efeito da resistência do ar é desprezado.
• Para a aceleração, temos que:
a g gĵ
v v0 gt
gt
y y 0 v0 t
2
2
2
v v0 2 gDy
2
Exemplo 1: Um corpo cai livremente a partir do repouso; calcule a sua
posição e velocidade em t = 1,0 , 2,0 , 3,0 e 4,0 s.
Resolução
1 2
y gt
2
e v gt
y0 0
v0 0
Em t = 1,0 s:
y = - 4,9 m
e
v = -9,8 m/s
Para outros valores do tempo, obtemos:
y
Exemplo 2. Uma pedra é arremessada verticalmente para cima no
ponto A do terraço de um edifício com uma velocidade inicial de
20,0 m/s. O prédio tem 50,0 m de altura. Determine: a) o tempo no
qual a pedra atinge a sua altura máxima, b) a altura máxima acima do
terraço e c) o tempo no qual a pedra retorna ao nível do arremessador.
a) o tempo no qual a pedra atinge a sua altura máxima
Quando a pedra atinge a altura máxima ela pára e
v v0 gt
então v=0 no ponto máximo
Substituindo o valor de v na equação fica
0 v0 gt
v0 gt
v 0 20,0 m/s
t
2,04 s
2
g 9,8 m/s
b) a altura máxima acima do terraço
y y0 v0t
1 2
gt
2
y0 0
t 2,04 s
Substituindo na equação fica
1
y (20 m/s)(2,04 s) (9,8 m/s 2 )( 2,04 s)2 20,4 m
2
c) o tempo no qual a pedra retorna ao nível do arremessador
y y0 v0t
y0 0
1 2
gt
2
y0
t0
1 2
1
0 v 0 t gt ( v 0 gt ) t
2
2
t 4,08 s