Corpos em queda livre

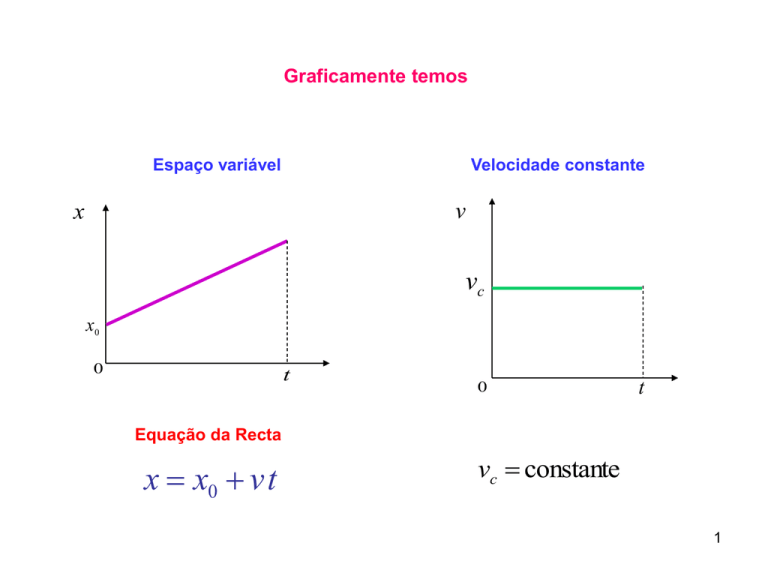
Graficamente temos
Espaço variável
Velocidade constante
v
x
vc
x0
0
t
0
t
Equação da Recta
x  x0  v t
vc  constante
1
Exemplos
Exemplo 6. O treinador de uma corredora determina sua velocidade enquanto ela corre
a uma taxa constante. O treinador inicia o cronómetro no momento em que ela passa
por ele e pára o cronómetro depois da corredora passar por outro ponto a 20 m de
distância. O intervalo de tempo indicado no cronómetro é de 4.4 s. a) Qual é a
velocidade da corredora? b) Qual é a posição da corredora 10 s após ter passado pelo
treinador?
a) Qual é a velocidade da corredora?
x  x0  v t
v
x0  0
t0=0
t = 4.4 s
x  x0 20 m - 0

 4.5 m/s
t
4.4 s
b) Qual é a posição da corredora 10 s após ter passado pelo treinador?
x  x0  v t  0  (4.5 m/s)(10 s)  45 m
2
Aceleração média
Quando a velocidade da partícula se altera,
diz-se que a partícula está acelerada
A aceleração média é a variação da velocidade
am 
v x num intervalo de tempo t
v f  vi
t f  ti
ou
v x
am 
t
3
Exemplo 8. Considere o movimento do carro da Figura 2. Para os dados apresentados
na Figura 2, calcule a aceleração média do carro.

a
Figura 2
v f  vi
A
velocidade
escalar
diminui com o tempo
15 m/s  30 m/s
am 

 7.5 m/s 2
t f  ti
2.0 s  0

v

a
4
Aceleração instantânea
Em algumas situações a aceleração média pode variar em intervalos de tempo diferentes
portanto é útil definir a aceleração instantânea
v dv
a  lim

t 0 t
dt
v

dv d  dx  d 2 x
a
   2
dt dt  dt  dt
Aceleração na direcção x
reta tangente à curva
da velocidade


a  aex

ex
t
x
5
Movimento rectilíneo uniformemente variado
Um movimento é uniformemente variado quando a aceleração é constante
v  v0  at
v0
é a velocidade da partícula
no instante t = 0
é a aceleração da partícula
é constante
se a velocidade da partícula aumenta com o tempo
o movimento é uniformemente acelerado
se a velocidade da partícula diminui com o tempo
o movimento é uniformemente retardado
Substituindo
dx
v
dt
Integrando fica
obtemos
dx
 v0  at
dt
1 2
x  x0  v0t  at
2
6
Exemplo 9. Um avião parte do repouso e acelera em linha recta no chão antes de levantar
voo. Percorre 600 m em 12 s. a) Qual é a aceleração do avião? b) Qual é a velocidade do
avião ao fim de 12 s?
a) Qual é a aceleração do avião?
x0  0
1 2
x  x0  v0t  at
2
Substituindo os valores
1 2
x  at
2
x0  0
v0  0
v0  0
(parte do repouso)
na equação
2 x 2  600 m 1200 m
2


8
.
3
m/s
 a 2 
t
144 s 2
122
b) Qual é a velocidade do avião ao fim de 12 s?
v0  0
v  v0  at


(parte do repouso)
v  at  8.3 m/s 2 12 s   100 m/s
7
Graficamente temos
Velocidade variável
Aceleração constante
x
a
v
Espaço variável
a
v0
x0
t
0
t
0
t
Parábola
Equação da recta
v  v0  a t
0
a  constante
1 2
x  x0  v0t  at
2
8
Corpos em queda livre
Galileo, o primeiro físico moderno, estudou a queda dos corpos
Refutou as hipóteses de Aristóteles
Através de experiências, mostrou que os corpos caem com a mesma
velocidade, independentemente de sua massa
9
Corpos em queda livre
Mas... devemos notar que em
geral, há outras forças actuando no
corpo considerado, o que pode
frustrar uma experiência se não
formos suficientemente cuidadosos
a
resistência
do ar!!
10
Corpos em queda livre
Vector aceleração da gravidade


g
O vector g aponta para baixo em
direcção ao centro da Terra

g
Valor da aceleração da gravidade
perto da superfície da Terra
g  9.8 m/s 2
As equações obtidas para partículas em movimento com aceleração constante são
aplicáveis ao corpo em queda livre. Assim
v  v0  gt
1 2
y  y0  v0t  gt
2
y
g

ey


g   ge y
11
y
Exemplo 10. Uma pedra é arremessada verticalmente para cima no
ponto A do terraço de um edifício com uma velocidade inicial de 20.0
m/s. O prédio tem 50.0 m de altura. Determine: a) o tempo no qual a
pedra atinge a sua altura máxima, b) a altura máxima acima do
terraço e c) o tempo no qual a pedra retorna ao nível do arremessador.
a) o tempo no qual a pedra atinge a sua altura máxima
Quando a pedra atinge a altura máxima ela pára e
v  v0  gt
então v=0 no ponto máximo
Substituindo o valor de v na equação fica
0  v0  gt

v0  gt

v0 20.0 m/s
t 
 2.04 s
2
g 9.8 m/s
b) a altura máxima acima do terraço
y  y0  v0t 
1 2
gt
2
y0  0
t  2.04 s
Substituindo na equação fica
1
y  (20 m/s)(2.04 s)  (9.8 m/s 2 )( 2.04 s) 2  20.4 m
2
c) o tempo no qual a pedra retorna ao nível do arremessador
y  y0  v0t 
y0  0
1 2
gt
2
y0
 t 0
1 2
1
0  v0t  gt  (v0  gt )t 
2
2
t  4.08 s