Ventos - Marcelo de Paula Corrêa

Ventos
Disciplina: Fundamentos de Meteorologia – EAM 10
Instituto de Recursos Naturais – Universidade Federal de Itajubá
Prof. Marcelo de Paula Corrêa
O que chamamos de vento ?
Quaisquer movimentos do ar atmosférico, que ocorrem naturalmente no interior do
fluido, à superfície ou a grandes alturas, podem ser designados genericamente como
VENTO!
No entanto, o VENTO é usualmente medido apenas pelas componentes horizontais de
sua velocidade. Estas componentes são importantes para o mecanismo termodinâmico
da atmosfera já que são eficientes para transportar calor, massa e momento.
A componente vertical, importante para formação de nuvens e precipitação, são
geralmente determinadas a partir das componentes horizontais. A grande dificuldade
para medi-la ou estimar as componentes verticais está na ordem de grandeza, cerca de
1000 vezes menor que as horizontais. Portanto, é útil separar o componente horizontal
do vento (leste-oeste e norte-sul) do componente vertical (para cima e para baixo).
As forças atuando sobre parcelas de ar são:
1) força do gradiente de pressão;
2) força de Coriolis;
3) força centrífuga;
4) a força de atrito; e
5) a força da gravidade.
Conceitos básicos
 Velocidades linear (v) e angular ()
v
v
v
S
S

e 
t
t
Como S  r  

r
S

r
t
t
S dS
d

r
 v  r
t 0 t
dt
dt
t  0  lim
 Força centrípeta (Fcp)
Lembrete!!! 1a Lei de Newton  v = constante se F=0
v
v
v1
v2

r
v1  v2
|v1| = |v2|
Conceitos básicos
a=acp + at
v1=v2=v

Força centrípeta (Fcp)
at  v
v1
v2
v1
at 

r
 d
lim


t 0 t
dt
então
 a

t v
v2
a  v   r 
r
2
v2
ou , na forma vetorial :


a  - 2 r
Conservação do momento angular (L)
O momento angular (L) de uma partícula em relação a um referencial é o produto vetorial
do vetor posição (r) pela quantidade de movimento (p) da dita partícula
L=rXp
onde: p = mv
e
L é perpendicular a r e p
Lei da conservação do momento angular: O momento angular de um sistema permanece
constante, a menos que seja aplicado um torque externo a esse sistema.
Conceitos básicos

Conservação do momento angular (L)

r=Rt cos
z
y

x
Rt
L

r
v
L=r X mv = r m v sen (90°) j
L=rv
(módulo por unidade de massa)
ou então….
r
v
L =  r2

L =  Rt2 cos2 
Exemplo: Uma parcela de ar no equador em
repouso em relação à superfície (v=  Rt).
Se essa parcela é forçada a se deslocar para
os pólos por meio de uma força dirigida para
o eixo de rotação ela chegará a latitude 
com velocidade v’=v/cos . Portanto terá uma
velocidade cada vez maior na direção L-O à
medida que se desloca para os pólos.
Forças fundamentais que atuam na atmosfera
 Força do gradiente de pressão (FGP)
(xo,yo,zo)
V=xyz
Fbx
Fax
z
x
y
p
x
x
p 

 Fbx  pS  Fax   p  x S
x 

Se p b  p  p a  p 
p 
p
p

Fx  Fbx  Fax  pS   p  x S 
xS 
V

x

x

x


Fx
1 p
como m  V 

m
 x
Como o mesmo pode ser escrito para as dimensões y e z, temos:
FGP
1  p p
p 
   i 
j  k 
m
  x y
z 
F
1
 GP   p
m

gradiente de pressão
representa a variação de uma grandeza escalar no espaço
p representa um vetor em O,
dirigido de B para A, portanto
com força de A para B.
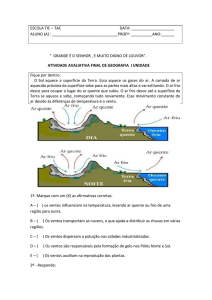
Exemplo:
BRISA MARÍTIMA
Forças fundamentais que atuam na atmosfera

Gravidade real e efetiva
(atração mútua entre os corpos)
GMm
Fg   2
r

Fg
GM
g* 
 2
m
r
Se a Terra está em rotação, a força indicada numa balança é geralmente menor,
em virtude do efeito centrífugo da rotação. Portanto, a gravidade efetiva é
simplesmente a soma da gravidade real (g*) com a aceleração centrífuga
g = g* + 2 r
Ao nível do mar e 45° de latitude: g = 9,80616 m/s2
Forças fundamentais que atuam na atmosfera

Forças de fricção ou viscosas
z=1
z=0
z
u(1)=uo
u(z)
L
uo
fluido incompressível
u(0)=0
fixa
y
A força tangencial aplicada sobre a placa
superior (Fr) e capaz de mantê-la em M.U. é
diretamente proporcional a área da placa e
inversamente proporcional a distância entre
as mesmas:
Auo
Fr 
L
x
Obs.: Para que o M.U. seja mantido cada camada horizontal deve exercer a mesma
força que a imediatamente inferior. Conseqüentemente, tomando o limite (z0), pode-se
escrever a força viscosa por unidade de área  Tensão de Cisalhamento (TC).
Fr
u
  zx  
A
z
onde :
u
u
u (1)  u (0)
 lim
 lim
z z 0 z z 0 z(1)  z(0)
zx expressa a componente da TC na direção x,
em razão do cisalhamento de escoamento do fluido
na direção z.
Isto é, representa o transporte de momento de cima
para baixo em virtude do movimento aleatório das
moléculas
Forças fundamentais que atuam na atmosfera

Forças de fricção ou viscosas – continuação
Fr
u
 zx  
A
z
é aplicada para um escoamento bi-dimensional,
incompressível e em estado permanente
Para o caso transiente, tem-se:
1 
 2u
 zx   2
 z
z
Se considerarmos todas as direções:

onde: == coef. visc. cinemática

F r   v

2

F r  K v
2
2
2



2  2  2  2
x
y
z
2
processos moleculares
processos turbulentos
operador Laplaceano
Forças fundamentais que atuam na atmosfera
 Força de Coriolis (Fco)

Surge como conseqüência de observarmos os movimentos
do ar num sistema de coordenadas não inercial, isto é, um
sistema de coordenadas fixo sobre a superfície, que gira
com ela
Movimento inercial como visto de um sistema newtoniano
(linha reta) e de um sistema em rotação (linha curva).
Exemplo: uma parcela de ar que se move na atmosfera
com um movimento relativo à superfície da Terra.
A força de Coriolis atua perpendicular ao vetor velocidade (relativo ao sistema em
rotação – Terra), podendo apenas mudar a trajetória da partícula e jamais a velocidade
Deflexão que ocorre no deslocamento Norte-Sul
Fco atua à direita de v no HN
e à esquerda de v no HS
PN
ΩTerra = 7,292 x 10-5 s-1
Deflexão que ocorre no deslocamento Oeste-Leste
Forças fundamentais que atuam na atmosfera
 Força de Coriolis (Fco) – expressão matemática
Considerando uma parcela de ar deslocando de Oeste para Leste com velocidade u em
relação à superfície,  a velocidade angular da Terra e R o vetor que liga o eixo de rotação
à parcela:
u << R

Força centrífuga
total que atua
=
sobre a partícula
por unidade de massa
2

u 
R u2 

2
    R   R  2u  2 R
R
R R

aceleração centrífuga devida
exclusivamente à rotação

Fco
R
 2u
m
R
forças defletoras que atuam
perpendicularmente ao eixo de rotação

sua ação é perpendicular
ao vetor velocidade !!!
PN2u cos
R
A parcela que
se desloca de
Leste  Oeste
terá:
aN-S= (dv/dt)co = – 2u sen
avertical = (dw/dt)co = 2u cos

Fco/m
2u sen
Forças fundamentais que atuam na atmosfera
 Força de Coriolis (Fco) – expressão matemática
Suponha agora que uma parcela se desloca ao longo de um meridiano, do pólo para o
equador. Como não existem torques de leste  oeste, então: R2 = constante!!!
Se R aumenta, então  vai diminuir e será desviada de leste para oeste
 aL-O= (du/dt)co = 2v sen = 2 fv
v  velocidade (spf) ao longo de um meridiano
De modo semelhante, uma partícula lançada para cima adquirirá em razão de Coriolis
uma aceleração zonal (ao longo de um paralelo) igual a – 2  w cos , onde w é a
componente vertical da velocidade da partícula (em relação à spf). Portanto, no caso
geral, a Fco contribuirá para acelerar o ar em diversas direções:
 aL-O= (du/dt)co = 2v sen – 2w cos
aN-S= (dv/dt)co = – 2u sen
avertical = (dw/dt)co = 2u cos
Fco= – 2  X v
v =u i + v j + w k
Forças fundamentais que atuam na atmosfera
 Força de Coriolis – quantitativamente
Imaginemos um foguete lançado do Polo Norte
para um alvo no equador (Fig. 7.6). Se o
foguete leva 1 hora para atingir o alvo, a Terra
terá girado 15° para leste durante o vôo. Para
alguém fixo sobre a Terra pareceria que o
foguete desviou sua rota e atingiu a Terra 15° a
oeste de seu alvo. Na realidade, a trajetória do
foguete foi reta e assim seria vista por um
observador fixo no espaço. Foi a rotação da
Terra que produziu, para um observador na
Terra, a aparente deflexão. Note que o foguete
foi desviado para a direita de seu percurso
devido à rotação anti-horária do HN (visto do
espaço). Rotação horária do HS (visto do
espaço) produz desvio para a esquerda.
Forças fundamentais que atuam na atmosfera
 Força de Coriolis – qualitativamente
V = 15 m/s
Ω = 7,292 x 10-5 s-1
Φ = 40°
Fco = 1,41 x 10-3 N/kg (m/s2)
 Obs:


a Força de Coriolis depende da latitude, sendo nula no
equador e máxima nos pólos (A rotação do nosso sistema
de referência é máxima nos pólos e diminui com a latitude,
até anular-se no equador).
A Força de Coriolis só é “sentida” em escalas de tempo de
duração comparável à rotação da Terra.
Forças fundamentais que atuam na atmosfera
Uma vez conhecidas as forças fundamentais, temos que:

dv

dt


F
  1
 
dv
 2   v  p  g  F r
dt

onde v representa a velocidade de uma
parcela de ar em relação à superfície da Terra
Expressando a equação acima em suas 3 componentes
zonal
meridional
vertical
u
u
u
u
1 p
u v w
 2v sen  2w cos  
  2 u
t
x
y
z
 x
v
v
v
v
1 p
 u  v  w  2u sen 
  2 v
t
x
y
z
 y
w
w
w
w
1 p
u
v
w
 2u cos  
 g   2 w *
t
x
y
z
 z
Forças fundamentais que atuam na atmosfera
 T 
 T 
 T 
 T 
T   t   x   y   z
 t 
 x 
 z 
 y 
derivada local
derivada total
Dividindo por t e fazendo t  0
T  T
T
T 
T 
  u
v
 w 
t  x
y
z 
T 
T 
 v T
t
advecção
Principais tipos de ventos
Vento geostrófico

Vento geostrófico: Escoamento horizontal, uniforme, paralelo às isóbaras e ocorre
nos níveis superiores da atmosfera, onde os efeitos de fricção são desprezíveis
Temosque:
então:
Lembrando
zonal zonal
u
u f vug  1 up
1 p
 u  v  w x  2v sen  2w cos  
  2 u
t
x
y
z
 x
1vp

v

v

v
1 p
2
f
u


meridional
g w

u

v


2

u
sen





v
meridional
zy
t
x
y
 y
No vento geostrófico FGP equilibra-se com Fco, resultando num escoamento com
E definindo:
f = 2 (v
g),sen

velocidade
constante
paralelo
às isóbaras. Portanto, no HN as baixas pressões
estarão sempre à esquerda do vento, e no HS, à direita (lei de Buys-Ballot)
Fco
p
HS
p – dp
Fgp
Principais tipos de ventos
Vento geostrófico
f vg 
1 p
 x
vg
f ug  
f Vg  
vg
1 p
 y
ug
Como o gradiente de pressão é normal às isóbaras, é comum se escrever:
f Vg  
1 p
Vg  
f n
1 p
 n
vg é proporcional ao G.P. e inversamente
proporcional à latitude e a densidade do ar
Obs: O vento geostrófico não é a melhor aproximação perto do equador e em
escoamentos excessivamente curvos (o que é frequente na atmosfera).
1 p
 y
Principais tipos de ventos
Vento geostrófico
Lei de Buys Ballot: “De costas para o vento no HN a pressão baixa
estará à esquerda e a pressão alta à direita. No HS a pressão alta
estará à esquerda e a pressão baixa à direita."
Obs: Essa lei é válida para vento em ar superior, deve-se ter cuidado
ao analisar ventos em superfície!
balanço geostrófico
Exercício – Vento geostrófico
Numa região próxima a 40° S as isolinhas de altura da superfície isobárica de 500 mb estão
orientadas leste-oeste e o espaçamento entre isolinhas adjacentes com diferença de 40 m
é 200 km, com altura decrescendo para o sul. Qual é a direção e velocidade do vento
geostrófico? (Exercício retirado da apostila de meteorologia básica Alice Grimm, 2005)
A velocidade do Vg é dada por:
FGP
1
1 p
  p  |FGP |
(horizontal)
m

 n
1 p
 2vgsen
 n
1
p 1 p
vg 

2sen n f n
| FGP || Fco |
Exercício – Vento geostrófico –
continuação
 dz 
dado !
 
 dn p500mb
Qual a relação com
pQR  0 
p
?
n
p
p
n 
z  0
n
z
p p
e
são ctes.
n z
 No lim(dist Q-R)  0  n  dn e z  dz
 Se n e z são pequenos, então
p
 dz 
n
    p
 dn p
z
Exercício – Vento geostrófico –
continuação
Pela equação hidrostática:
p
  g
z
tem-se que:
1 p
1 p
 dz 
 dz 

ou

g
 
 
 n
 dn p g n
 dn p
1 p
z
g
 n
n
z
 dz 
(em coordenada s isobáricas)
  
dn

n
 p
Substituindo em vg →
vg 
g
z g z

2sen n f n
Com g = 9,8 m/s2, Ω = 7,292x10-5 s-1, Φ = 40°,
vg = 20,9 m/s

z
 2.104 m / m
n
Direção: O  L
Principais tipos de ventos
Vento gradiente
isóbaras não são
linhas retas
células
aproximadamente
circulares
centro circulares de
alta e/ou baixa pressão
ALTERA A VELOCIDADE
FORMA DO CAMPO
DE PRESSÃO
MODIFICA O
VENTO GEOSTRÓFICO
DIREÇÃO CONTINUA
// ISÓBARAS
Principais tipos de ventos
Vento gradiente
adaptado de Grimm, 2005
Balanço entre:
anti-ciclones
FGP, Fco, Fc
(Fc = v2/R)
ciclones
Centros de Baixa Pressão: CICLONES
Centros de Alta Pressão: ANTI-CICLONES
Principais tipos de ventos
Vento gradiente
Vento gradiente: Escoamento horizontal, paralelo às isóbaras, as quais são curvas, e
ocorre nos níveis superiores da atmosfera. Para um observador fixo na Terra, tais
escoamentos são associados a uma força centrífuga (v2/R), resultante entre a Fco e FGP
anti-ciclônico
ciclônico
anti-horário
horário
escoamento gradiente
v
HN
A
Fco
Fgp
B
Fc
Fgp
Fco
Fc
v
anti-ciclônico
ciclônico
horário
anti-horário
v
HS
B
Fgp
Fco
Fc
A
Fco
Fgp
Fc
Principais tipos de ventos
Vento gradiente
Velocidade do vento gradiente em torno de uma alta pressão
Fco  FGP  Fc
v = (Rf/2) – ...
v = (Rf/2) + ...
1 p v 2
fv 

 n R
R p
v 2  Rfv 
0
 n
Rf
R 2 f 2 R p
v


2
4
 n
 p
Rf 2 



4 
 n
Para que haja equilíbrio numa alta:
GP deve ser limitado  tornando-se cada vez menor em direção ao centro (R ↓)
Principais tipos de ventos
Vento gradiente
Velocidade do vento gradiente em torno de uma baixa pressão
FGP  Fco  Fc
v = (– Rf/2) + ...
v = (– Rf/2) – ...
1 p v 2

 fv
 n R
R p
2
v  Rfv 
0
 n
Rf
R 2 f 2 R p
v


2
4
 n
Não há limitação para que haja equilíbrio numa baixa.
É comum a ocorrência de fortes baixas pressões com fortes gradientes de pressão e fortes ventos
associados, enquanto os centros de alta pressão são normalmente mais "achatados", com gradiente de
pressão e ventos associados mais fracos.
Exercício – Vento gradiente
Numa região a 50 km do centro de um intenso furacão, há um gradiente de
pressão radial de 50 mb por 100 km. A temperatura está localizada em 20° N.
Calcule as velocidades dos ventos geostrófico e gradiente.
(Exercício retirado da apostila de meteorologia básica Alice Grimm, 2005)
f = 2 Ω sen20° = 4,98.10–5 s
ρ = 1,25 kg/m3
∂p/∂n = 50*102/105 = 0,05 Pa/m
Fc >> Fco
vg = (1/ρf)(∂p/∂n) = [1/(1,25* 4,98.10–5)]*(0,05) = 820 m/s
Se as trajetórias do ar forem consideradas circulares em torno do centro da
temperatura:
2
Rf
 Rf  R p
v
   
2
 n
 2 
Com R = 50.103 m → v = 43,5 m/s (situação anômala) ou
v = – 46,0 m/s (situação normal, em torno da BP)
Principais tipos de ventos

Vento ciclostrófico: Escoamento atmosférico curvo (em relação à superfície) de escala
horizontal suficientemente pequena (tornados e redemoinhos), em que Fco pode ser
desprezada quando comparada com FGP
Só ocorre em torno de um centro de baixa pressão (escoamento ciclônico). Tal
escoamento é um caso particular do escoamento gradiente em que f = 0.
fr  fr   r  p 
v g         
2  2     n 
2
1
2
 r  p 
v c    
   n 
1
2
Exemplo: Tornados. Fenômenos de pequeno raio (~300m) e ventos fortes (+ 100km/h).
Embora Fco seja desprezível, no HN os tornados giram no sentido anti-horário,
enquanto que no HS giram no sentido horário. Isso se deve a atuação de Fco no início
do processo de formação. Em vórtices menores, como nos redemoinhos, Fco não age
e, portanto, o giro ocorre em qualquer sentido.
Principais tipos de ventos

Vento térmico: diferença entre o vento geostrófico entre duas superfícies isobáricas. A
denominação vento térmico se deve ao fato de que ele somente existe se houver um
gradiente horizontal de temperatura ao longo das superfícies isobáricas.
O vento térmico entre dois níveis Z1 e Z2 é matematicamente expresso por:
R 
  p1 
v T   k   p T  ln  
f 
  p2 

Obs: Embora o regime de ventos na média e alta troposfera seja bastante diferente
em relação à baixa atmosfera, tais regimes estão relacionados entr si por meio da
temperatura média da camada de ar. Isto é matematicamente demonstrado
combinando-se a equação do estado com a do equilíbrio hidrostático:
p
 gp
 g 
z
RT
Ventos próximos à superfície
 ATRITO



Importante nos 1os km da atmosfera
↓v e, portanto, ↓Fco
↓v e, portanto, FGP permanece a mesma
FGP > Fco
Portanto, o ar cruzará as isóbaras em direção à área de menor pressão.
Ψ ~ 10° (oceanos) a Ψ ~ 45° (terreno rugoso)
Ventos próximos à superfície
ciclone em superfície no HS
anti-ciclone em superfície no HS
B
A
CONVERGÊNCIA
DIVERGÊNCIA
Dispositivos para medição do vento
 Anemometria: Determinação quantitativa do vento, em termos do
módulo de sua velocidade e direção.
 Observação do vento à superfície

Catavento de Wild: Grosseiro instrumento mecânico, constituído por um
detector de direção (grimpa) e um indicador de velocidade. São
instalados em um mastro a cerca de 10m do solo. A grimpa possui um
contrapeso e duas aletas. Quatro varetas abaixo da grimpa dão as
direções dos pontos cardeais. O indicador de velocidade é uma placa
presa ao próprio eixo de rotação da grimpa, mantendo-se sempre
perpendicular ao vento.

Anemômetros (indicadores) e anemógrafos (registradores) de conchas:
Possuem 3 ou 4 conchas, hemisféricas ou cônicas, de metal dispostas
simetricamente num plano horizontal. O movimento circular aciona um
gerador elétrico (anemômetros auto-geradores) ou um contador de voltas
(anemômetros totalizadores – velocidade média). Uma das restrições se
deve a inércia, já que as conchas precisam que o vento atinja certa
velocidade par aque iniciem a rotação. O inverso pode ocorrer após uma
rajada forte.
Dispositivos para medição do vento

Observação do vento à superfície

Anemômetros e anemógrafos termoelétricos: São mais precisos. Têm como
elemento sensível a platina ou o tungstênio.
 Em alguns modelos o sensor, mantido à temperatura constante, é exposto ao vento e a
velocidade é obtida através da medição da corrente elétrica necessária para manter a
temperatura constante.
 Em outros a corrente é que se mantém constante e a variação da temperatura é o termo
dependente da velocidade do vento.
 Ambos são usados em locais onde o deslocamento do ar é pequeno, como no interior de
culturas agrícolas. São pequenos e fáceis de ser instalados até mesmo em mastros para
determinação da variação vertical da velocidade.

Anemógrafo universal: Instrumento mecânico que serve para registrar a
direção e as velocidades instantânea e média do vento. Possuem 3 sensores
e 4 penas registradoras. O sensor de direção é uma grimpa conectadas a
alavancas, o de velocidade são conchas e a rotação das mesmas mede a
distância percorrida. A velocidade instantânea é medida através de um tubo
de pitot que aciona a quarta pena registradora. É de grande porte e servem
para registrar ventos a 10m de altura cuja velocidade de direção são
requeridas para estudos sinóticos. Não são usados para perfis.
Dispositivos para medição do vento

Observação do vento à superfície


Anemômetros sônico: Consistem de três pares de emissores-receptores de
sons ortogonais. Cada par é capaz de detectar sutis variações entre emissões
e recepções de sons. A velocidade de escoamento é deduzida indiretamente a
partir das alterações provocadas. Pode ser instalado de maneira a medir
componentes orientadas do vento (L-O, N-S, etc.) passando a fornecer as
componentes zonal, meridional e vertical da velocidade do ar.
Observação do vento em níveis elevados da atmosfera
Utiliza-se sensores acoplados a balões

Sondagens ópticas: Medindo-se o ângulo de elevação e o azimute do balão
em intervalos regulares é possível estimar sua trajetória. Existem diversos
problemas relacionados ao método, tais como a presença de nuvens.

Radioventossondas: Sucessivas posições de uma radiossonda em vôo,
obtidas eletronicamente.
Escalas de sistemas meteorológicos
Tipo
rajadas
redemoinhos
tempestades
linhas de instabilidade
ciclones/anti-ciclones
ondas planetárias
Dimensão
~cm
~m
km
10-100 km
100-1000 km
globo
Tempo
~s
~min
~1h
~1 dia
vários dias
sazonais
Perguntas…
 Quando a força de Coriolis que atua sobre uma parcela que se
desloca em relação à superfície da Terra, em qualquer latitude,
é exatamente igual a zero ?
 Considere um centro de alta pressão, em larga escala espacial,
no HS. Em que sentido o ar deve circular em torno deste centro,
na alta atmosfera ? Pode ocorrer circulação no sentido oposto ?