Slide 1 - Google Sites

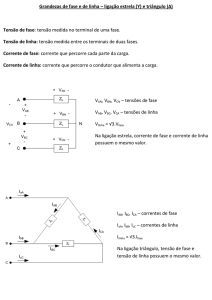
LEI DE OHM
FIO
CONDUTOR
CORRENTE ELÉTRICA (I)
TENSÃO ELÉTRICA (V)
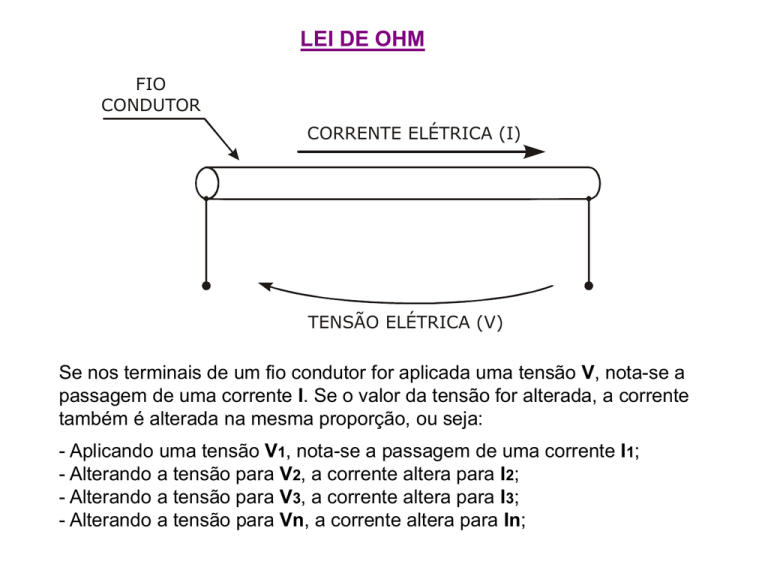
Se nos terminais de um fio condutor for aplicada uma tensão V, nota-se a
passagem de uma corrente I. Se o valor da tensão for alterada, a corrente
também é alterada na mesma proporção, ou seja:
- Aplicando uma tensão V1, nota-se a passagem de uma corrente I1;
- Alterando a tensão para V2, a corrente altera para I2;
- Alterando a tensão para V3, a corrente altera para I3;
- Alterando a tensão para Vn, a corrente altera para In;
Nota-se que a relação entre a tensão e o respectivo valor de corrente é uma
constante:
TENSÃO
(V)
V1 V2 V3
V


 ...... n
I1
I2
I3
In
Vn
V4
V3
V2
V1
I1
I2
I3
I4
In
CORRENTE
(I)
À relação entre a tensão e o respectivo valor de corrente denomina-se como
sendo a resistência elétrica (R).
R 
V
I
(em ohms ou )
ANÁLISE DE CIRCUITOS ELÉTRICOS
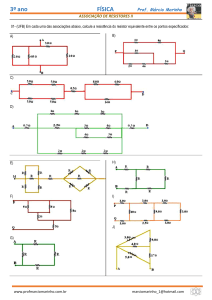
1. DEFINIÇÕES: Na análise de circuitos elétricos são utilizados termos e
denominações como veremos a seguir:
a) Bipolo elétrico – Qualquer dispositivo elétrico com dois terminais
acessíveis para conexão elétrica;
b) Gerador de tensão contínua – Bipolo capaz de manter constante a tensão
(V) em seus terminais, seja qual for o valor da corrente (I) que passa por ele:
I
V
Notar que as setas da tensão (V) e da corrente (I) têm o mesmo sentido.
c) Bipolo receptor – Recebe energia elétrica e a transforma em outro tipo de
energia (calor, luz, força mecânica). Em corrente contínua utilizaremos dois
tipos de bipolo receptor:
 Resistor:
I
I
V
R (
I
I
V
V
R (
I
Notar que as setas têm sentidos contrários.
 Força contra eletromotriz (f.c.e.m.):
(bateria recebendo carga)
I
V
d) Circuito elétrico – Conjunto de bipolos interligado de maneira a permitir a
existência de corrente elétrica:
B
A
G
R1
R5
R2
VA
R6
C
F
H
VB
R7
R4
E
R3
D
R8
I
e) Ponto elétrico – Ponto de conexão entre dois bipolos. No exemplo temos os
pontos elétricos: A, C, E, F, G, H e I
f) Nó – Ponto de conexão entre três ou mais bipolos. No exemplo temos os nós:
BeD
B
A
G
R1
R5
R2
VA
R6
C
F
H
VB
R7
R4
E
R3
D
R8
I
Ramo – Trecho compreendido entre dois nós consecutivos. No exemplo temos
os ramos:
 Ramo 1: B, A, F, E e D
 Ramo 2: B, G, H, I e D
 Ramo interno: B, C e D
B
A
G
R1
R5
R2
VA
R6
C
F
H
VB
R7
R4
E
R3
D
R8
I
Malha – Qualquer contorno fechado que pudermos definir no circuito, sem
que se passe duas vezes pelo mesmo ponto. No exemplo temos as malhas:
 Malha 1: A, B, C, D, E, F e A
 Malha 2: B, G, H, I, D, C e B
 Malha externa: A, B, G, H, I, D, E, F e A
2. LEIS DE KIRCHHOFF: Aplicada na análise de circuitos elétricos, são duas leis:
a) Lei dos nós (ou lei das correntes): “Em um nó, a soma das correntes que
chegam a este nó é igual à soma das correntes que saem deste nó.”
ΣIchegamao nó  ΣIsaemdo nó
I1
A
I1
I3
B
R1
I2
G
R5
R2
R6
Efetuando a análise nos nós B e D:
VA
C
F
I3
H
VB
R7
R4
 Nó B: I1 = I2 + I3
I2
E
R3
I1
D
I3
R8
I
 Nó D: I2 + I3 = I1
b) Lei das malhas (ou lei das tensões): “Em uma malha, a soma das
tensões indicadas no sentido horário é igual à soma das tensões indicadas no
sentido anti-horário.”
ΣVsentido horário  ΣVsentido anti-horário
V1
V5
B
A
G
R1
R5
V2
VA
V4
C
malha 2
R6
V7
V3
R3
R7
V8
D
R8
 Malha 1:
VA = V1 + V2 + VB + V3 + V4
H
VB
R4
E
V6
R2
malha 1
F
Efetuando a análise nas malhas 1, 2
e externa:
 Malha 2:
VB + V2 = V5 + V6 + V7 + V8
I
 Malha externa:
VA = V1 + V5 + V6 + V7 + V8 + V3 + V4
RESOLUÇÃO DE CIRCUITOS EM CORRENTE CONTÍNUA
Resolver um circuito elétrico significa determinar as tensões e
correntes deste circuito. Dentre os métodos existentes para
resolução de circuitos (associação de resistores, Norton/Thévenin,
malhas, nós, superposição de efeitos etc.) utilizaremos o método da
associação de resistores.
Método da associação de resistores – Este método é utilizado
quando o circuito possui uma ou mais fontes de tensão em apenas
um ramo do circuito (em apenas um ramo do circuito pode existir
fontes de tensão).
Exemplo: Resolver o circuito a seguir, determinando todas as
tensões e correntes:
VG
160 V
R1
R3
20
40
R2
150
R4
60
a) Para facilitar a visualização das tensões, recomendo nomear todos
os pontos e nós do circuito com letras (A, B, C, D, .....). Notar que a
letra dos pontos somente muda após um resistor ou gerador:
A
R1
B
R3
C
R2
VG
R4
D
D
C
b) Indicando as tensões e correntes. No gerador as setas das
tensões e correntes têm mesmo sentido. Nos resistores as setas
das tensões e correntes têm sentidos contrários:
VBC
VAB
R1
A
IT
I1
B
IT
C
I2
R2
VG
VBD
I2
IT
D
R3
I1
R4
D
C
VCD
c) Calcular a resistência equivalente da associação série ou
paralela de resistores mais evidente:
VBC
VAB
R1
A
IT
IT
C
I2
R2
VG
VBD
I2
IT
D
R3
I1
B
I1
R4
D
figura 1
C
VCD
Req1 = R3 + R4
Req1 = 40 + 60 = 100Ω
d) Redesenhar o circuito e calcular a próxima resistência equivalente:
VAB
R1
A
IT
I1
B
IT
B
I2
R2
VG
VBD
IT
VBD
Req1
I1
D
D
D
figura 2
R eq2 
R2 x R eq1
R2  R eq1

150 x R eq1
150  R eq1
150 x 100

 60
150  100
d) Redesenhar o circuito novamente e calcular a próxima resistência
equivalente:
VAB
R1
A
B
IT
IT
VBD
Req2
VG
ReqT = R1 + Req2 = 20 + 60 = 80Ω
IT
D
A
D
figura 3
A
IT
IT
VG
ReqT
VG
IT
D
figura 4
D
e) A partir da última figura, calcular a tensão ou corrente incógnita até
a figura original.
A
A
IT
IT
VG
ReqT
VG
IT
D
- na figura 4:
figura 4
D
VG
160
IT 

 2A
R eqT
80
IT  2A
VAB
JÁ CALCULADO:
R1
A
B
IT = 2A
IT
IT
VBD
Req2
VG
IT
D
D
figura 3
- na figura 3: VAB = R1 x IT = 20 x 2 = 40V
VBD = Req2 x IT = 60 x 2 = 120V
VAB = 40V
VBD = 120V
VAB
R1
A
IT
I1
B
IT
JÁ CALCULADO:
B
IT = 2A
VAB = 40V
VBD = 120V
I2
R2
VG
VBD
IT
VBD
Req1
I1
D
D
D
figura 2
- na figura 2:
VBD 120

 1,2A
R eq1 100
I1 = 1,2A
VBD 120
I2 

 0,8A
R2 150
I2 = 0,8A
I1 
VBC
VAB
R1
A
IT
I1
B
IT
C
I2
R2
VG
IT = 2A
VAB = 40V
VBD = 120V
I1 = 1,2A
I2 = 0,8A
VBD
I2
IT
D
R3
JÁ CALCULADO:
I1
R4
D
figura 1
C
VCD
- na figura 1: VBC = R3 x I1 = 40 x 1,2 = 48V
VCD = R4 x I1 = 60 x 1,2 = 72V
VBC = 48V
VCD = 72V
Métodos de verificações – Tais métodos são utilizados para
verificação dos resultados calculados na resolução de circuitos.
Podemos utilizar dois métodos:
a) Análise de malhas – Consiste em aplicar a 2ª Lei de Kirchhoff
(Lei das malhas ou das tensões) em todas as malhas.
ΣVsentido horário  ΣVsentido anti-horário
b) Balanço energético – É a aplicação do princípio da conservação de
energia, isto é, a soma da potência dos geradores de tensão é igual à
soma das potências nos resistores.
ΣPGERADORES  ΣPRESISTORES
Exemplo de aplicação dos métodos de verificações:
No exemplo anterior, temos as tensões e correntes calculadas:
VBC
VAB
B I1
A
IT

I2
VBD
160 V
C
50
150
malha 1
malha 2

D
D
C
VCD
IT = 2A
I1 = 1,2A
I2 = 0,8A
VAB = 40V
VBD = 120V
VBC = 48V
VCD = 72V
a) Verificação por análise de malhas:
ΣVsentido horário  ΣVsentido anti-horário
Efetuando a análise nas malhas 1, 2 e externa:
VBC
VAB
B I1
A
IT

I2
VBD
160 V
C
160 = 40 + 120
160 = 160 
50
150
malha 1
malha 2
 Malha 2: VBD = VBC + VCD

D
D
C
VCD
 Malha 1: 160 = VAB + VBD
120 = 48 + 72
120 = 120 
 Malha externa: 160 = VAB + VBC + VCD
160 = 40 + 48 + 72
160 = 160 
Portanto, conclui-se que os resultados estão corretos.
b) Verificação por balanço energético:
IT = 2A
I1 = 1,2A
I2 = 0,8A
ΣPGERADORES  ΣPRESISTORES
VAB = 40V
VBD = 120V
VBC = 48V
VCD = 72V
PGERADORES
PGERADORES
GERADORES
P
P
GERADORES
(P
G
=
V
xGGIx
Tx) IG)
P
GERADORES
P
GERADORES
(P
G=
=G VV
(P
G
IG)
P
GERADORES
(P=G
V
x IG)
G=
=VG
V
GIG
(P(P
G(P
xG
G =VG
x xI)GI)G)
PRESISTORES
PRESISTORES
RESISTORES
P
P
RESISTORES
(P
R
=
V
R
P
RESISTORES
P
RESISTORES
(P
=xVVRIRRx)x IIRR))
(P
RR =
P
RESISTORES
(P
R
=
V
R
x
RV
=
V
RIR
xI)RII)RR))
(P
R(P
=
R
x
(P
R
=
V
R
x
P
R1
=
V
AB
x
I
T
=
PR1 = VAB x IT =
P
R1
=
V
AB
x=
IITT =
P
R1
=AB
V
AB
=
PR1
=
V
I=
Tx
==40
40
=
80W
=
xxx
22
PR1
V
AB
x
I
T80W
=
=
40
x
=
80W
=40
40
x2=2
2=80W
=80W
80W=
==40
x x2=
R2
=
BC
PPR2
VV
BC
xx II11 =
160 xx 22 =
= 320W
320W
P
R2
=
V
BC
II11 =
160
P=
R2
=BC
V
BC
xI1=
=
PR2
=
V
x
I1x
=
48
x
1,2
==57,6W
57,6W
160
x
2
=
320W
48
x
1,2
=
P
R2
=
V
BC
x
160
x
2
=
320W
160
x
2
=
320W
=
48
x
1,2
=
57,6W
160 x 2 = 320W
=48
48
x1,2
1,2
=
57,6W
==48
x x1,2
=57,6W
R3
=
CD
=
PPR3
=
VV=
CD
xx57,6W
II11 =
P
R3
=
V
CD
x
I
1
=
P=
R3
=CD
V
I=1=86,4W
=
PR3
=
V
x1,2
I1xI1=
==72
72
1,2
86,4W
xxCD
=
PR3
V
CD
x
=
72
x
1,2
=
86,4W
=72
72
x1,2
1,2
=
86,4W
==72
x x1,2
=86,4W
R4
=
BD
=
PPR4
=
VV=
BD
xx86,4W
II22 =
P
R4
=
V
BD
x
I
2
=
P=
R4
=BD
VBD
I2=
PR4
=
V
x
I0,8
2x
==120
120
==96W
96W
xxx0,8
PR4
VBD
I2=
=
120
x
0,8
=
96W
=120
120
x0,8
0,8
=96W
96W
==120
x x0,8
==96W
PGERADORES
GERADORES =
= 320W
320W 

PRESISTORES
RESISTORES =
= 320W
320W 

P
P
P
GERADORES
=
320W

P
RESISTORES
=
320W

P
GERADORES = 320W
P
RESISTORES = 320W
P
GERADORES
P
RESISTORES
P
GERADORES==320W
320W
P
RESISTORES==320W
320W
Portanto, conclui-se que os resultados estão corretos.
FIM DA APRESENTAÇÃO