x,fa

Conceitos de Sinais e Sistemas
Mestrado em Ciências da Fala e da Audição
Edição 2006/7
António Teixeira
AT 2006
1
Aula
AT 2006
•
Conversão A/D
•
Aliasing
•
Quantização
•
Conversão D/A
•
Operações com sinais
•
Som em Matlab
2
Passagem de contínuo a discreto
AT 2006
3
Conversão A/D
• O processo pelo qual um sinal é convertido
numa representação digital é conhecido por
conversão analógica-digital
– A/D conversion
• O processo inverso D/A
AT 2006
4
Passagem de contínuo a discreto - Amostragem
10
9.08
8.16
8
8.08
7.40
6.46
6.02
6
6.52
4
2.80
2.52
1.95
2
0.14
0 0.00
-0.6
-2
AT 2006
0
20
40
60
80
100
120
140
5
Amostragem
10
9.08
8.16
8
8.08
7.40
6.46
6.02
6
6.52
4
2.80
2.52
1.95
2
0.14
0 0.00
-0.6
Período de amostragem
-2
AT 2006
0
20
40
60
80
100
120
140
6
Amostragem
• Tira-se amostras do sinal espaçadas de um intervalo
de tempo fixo, o período de amostragem,
representado por Ta
• O período de amostragem depende da frequência de
amostragem (fa) [em Inglês fs]
– Número de amostras por segundo
– Ex: fa=1000 Hz dá T=1/fa=1/1000=1 ms
• O número total de pontos de um sinal digital depende
da sua duração e da frequência de amostragem
– 5 segundos amostrados a 10 000 Hz dão 50 000 amostras
AT 2006
7
Sinal Discreto
O sinal anterior pode ser representado de
forma aproximada apenas pela amplitude das
suas amostras e pelo período de amostragem.
S= [0, 1.95, 7.4, 9.08, 8.16, 6.03, 2.8,
0.15, -0.68, 2.53, 6.46, 8.09, 6.52]
Ou seja, pode ser representado por um vector
AT 2006
8
Uma sinusóide de 2.5 Hz amostrada
fa=40 Hz
1
0
-1
0
0.1
0.2
0.3
0.4 fa=6
0.5Hz
0.6
0.7
0.8
0.9
1
0
0.1
0.2
0.3
0.4 fa=4
0.5Hz
0.6
0.7
0.8
0.9
1
0
0.1
0.2
0.3
0.4
0.6
0.7
0.8
0.9
1
1
0
-1
1
0
-1
AT 2006
0.5
9
Teorema de Nyquist
• Apenas ficar com algumas amostras do sinal
não leva a perder informação contida no sinal
analógico ?
– Nyquist mostrou que sinais com largura de banda
limitada – que contêm apenas uma certa gama de
frequências – podem ser reconstruídos
EXACTAMENTE do sinal amostrado desde que a
FREQUÊNCIA DE AMOSTRAGEM SEJA O
DOBRO da maior frequência contida no sinal
AT 2006
10
Exemplo
• Seja 100 Hz a frequência mais elevada contida
num sinal analógico
– Qual deve ser a frequência de amostragem a
utilizar ?
– Estes 100 Hz podem corresponder a algum sinal
que conhece da área da voz ?
• E no caso do sinal de voz ?
AT 2006
11
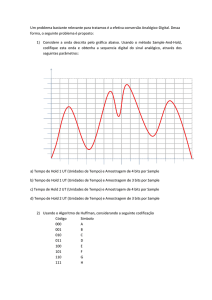
Aliasing
O que acontece se não se respeitar o
Teorema ?
AT 2006
12
“Aliasing”
• Se usarmos uma
frequência inferior a 2x
a maior frequência
contida no sinal ocorre
o chamado “aliasing”
• Exemplo:
– Sinusóide de 14 Hz
– Sinusóide de 4 Hz
– Ambas amostradas a 10
Hz
– Amostras são as mesmas
AT 2006
1
0.5
0
-0.5
-1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1
0.5
0
-0.5
-1
13
O que acontece se não se amostra
suficientemente rápido?
x(t)=A cos (2f0t+)
se amostramos com um período Ts obtemos
x[n]=x(nTs)=A cos (2f0nTs+)
Consideremos outra sinusóide com frequência f0+k fs, com k inteiro e fs=1/Ts
y(t)=A cos (2(f0+k fs)t + )
Amostrando y(t) com o mesmo Ts, obtemos
y[n]=y(nTs)
=A cos (2 (f0+k fs) nTs+)
= A cos (2f0 nTs+ 2 k fs Ts+)
= A cos (2f0 nTs+ 2 k +)
= A cos (2f0 nTs +)
= x[n]
y[n] tem as mesmas amostras que x[n] sendo impossível distingui-la de x[n].
Como k é um inteiro, positivo ou negativo, existem um número infinito de
sinusóides que resultam nas mesmas amostras x[n] quando amostradas com
a frequência fs !
AT 2006
14
O que acontece se não se amostra
suficientemente rápido?
Considermos uma sinusóide de frequência f: x(t)=A cos (2f0t+)
se amostramos com um período Ts obtemos
x[n]=x(nTs)=A cos (2f0nTs+)
Consideremos outra sinusóide com frequência f0+k fs, com k inteiro e fs=1/Ts
y(t)=A cos (2(f0+k fs)t + )
Amostrando y(t) com o mesmo Ts, obtemos
y[n]=y(nTs)
=A cos (2 (f0+k fs) nTs+)
= A cos (2f0 nTs+ 2 k fs Ts+)
= A cos (2f0 nTs+ 2 k +)
= A cos (2f0 nTs +)
= x[n]
y[n] tem as mesmas amostras que x[n] sendo impossível distingui-la de x[n].
Como k é um inteiro, positivo ou negativo, existem um número infinito de
sinusóides que resultam nas mesmas amostras x[n] quando amostradas com a
frequência fs !
AT 2006
15
alias
• As frequências f0+k fs são chamadas “alias” da
frequência f0
• porque todas elas parecem ser a mesma quando
amostradas com frequência de amostragem fs
• No dicionário Inglês-Português da Porto Editora:
– alias [´eiliaes] , 1 adv. aliás
2 s. pseudónimo, nome falso, nome suposto
AT 2006
16
Uma segunda fonte de “aliasing” - “folding”
Considerando sinusóide de freq. f: x(t)=A cos (2f0t+)
se amostramos com um período Ts obtemos
x[n]=x(nTs)=A cos (2f0nTs+)
Consideremos outra sinusóide com frequência -f0+k fs, com k
inteiro e fs=1/Ts
w(t)=A cos (2(-f0+k fs)t + )
Amostrando y(t) com o mesmo Ts, obtemos
w[n]=y(nTs) =A cos (2 (-f0+k fs) nTs+)
= A cos (-2f0 nTs+ 2 k fs Ts+)
= A cos (-2f0 nTs+ 2 k +)
= A cos (2f0 nTs +) % porque cos(- )=cos()
= x[n]
w[n] tem as mesmas amostras que x[n] sendo impossível
distingui-la de x[n].
AT 2006
17
Porquê “folding”
freq.
aparente
1000
1000
2000
Frequência real
AT 2006
18
Aliasing
• Sendo f a frequência de um sinal e a frequência de
amostragem fs, as seguintes regras permitem calcular
a frequência
• f < ½fs
• Como a frequência do sinal se encontra abaixo do limite imposto
pelo teorema da amostragem, não ocorre “aliasing”; o sinal
amostrado possui a frequência correcta.
• ½fs < f < fs
• Existe “aliasing” sendo a frequência do sinal amostrado fa = fs - f
• f > fs
• Ocorre “aliasing”. Para obter a frequência do sinal amostrado obter
o resto da divisão de f por f. No final se ½fs < f < fs o sinal
amostrado fa = fs - f ; caso contrário fa = f
AT 2006
19
Aliasing
freq digital
5k
5k
AT 2006
10k
15k
freq real
20
Quantização
AT 2006
21
Quantização
• Os valores contínuos da amplitude também
têm de ser convertidos em valores tratáveis
pelo computador
– Os computadores guardam os números usando 0s e
1s, os chamados bits
– 3 bits dá para representar 8 números diferentes
• 000 001 010 011 100 101 110 111
• Este processo designa-se por quantização
AT 2006
22
Precisão, número de bits
• O número de bits usados para representação
determina a precisão (ou resolução) em amplitude do
processo de amostragem referido atrás.
• Quanto mais bits forem usados, maior será essa
resolução.
• Para obtermos uma resolução equivalente à de um
sistema CD de áudio, são necessários 16 bits,
– o que significa que temos 65536 combinações
numéricas possíveis.
– Os valores de amplitude amostrados são sempre
arredondados para o código binário mais próximo.
AT 2006
23
Exemplo de quantização
• 8 bits
1
0
-1
• 7 bits
1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
-1
• 3 bits
1
0
-1
• 2 bits
1
0
-1
AT 2006
24
Em Matlab
t=0:1e-3:4
x= sin (2*pi*10*t)+1 % para ser entre 0 e 1
bits=1
N=2^bits
xquant=round(x*(N-1)/2)*2/(N-1)
stem(t,xquant,'ro'); hold on;
diferenca=x-xquant
plot(t,diferenca, 'g+')
% experimente com bits=1,2 ...
AT 2006
25
Resultados
4 bits
2 bits
erro
8 bits
AT 2006
26
Exemplo
•3 bits
AT 2006
27
Número de bits
• 8 bits
– 256 níveis
– Se tivermos sinal entre – 1 e + 1 V
• Erro máximo 3.4 mV (mili=0.001)
• 16 bits
– 65536 níveis
– Se tivermos sinal igual ao anterior
• Erro máximo 15 microV (micro=0.000001)
AT 2006
28
Erro de arredondamento e bits
1
•N=níveis
• = distância entre
níveis
-1
N=2/
N  =2
 =2/N
Erro máximo de arredondamento é = /2=1/N
logo N=1/ 
número de bits (b)  b log2 N
AT 2006
29
SNR devido a quantização
SNR= 20 log10 (App/)
como A=2 e N=2b temos = 2-b
App/= 2 x 2b = 2b+1
logo 20 log10 (2b+1) = 20 (b+1) log10 (2)
6 (b+1) dB
aumento de 6 dB/bit
AT 2006
30
Em Matlab
% RETOMANDO O EXEMPLO ANTERIOR
t=0:1e-3:4;
x= sin (2*pi*10*t);
bits=9;
N=2^bits;
xquant=round(x*(N-1)/2)*2/(N-1);
plot(t,xquant,'ro'); hold on;
diferenca=x-xquant;
plot(t,diferenca, 'g+');
% valor do erro máximo de arredondamento neste caso concreto
max(diferenca)
% valor teórico para o erro máximo de arredondamento
1/N
% SNR
snr=10*log10(dot(x,x)/dot(diferenca,diferenca))
% EXPERIMENTE com 1,2 ... até 8 bits. Qual o aumento de snr
com o aumento de 1 bit ?
AT 2006
31
Exercício
• Estimar o número de bits necessários para
representar amostras de um sinal com valores
entre –1 e 1 com um erro de arredondamento
inferior a 10-3
AT 2006
32
Quantos Hz ? Quantos bits ?
• Para sinal de voz ?
• Para música (CD) ?
– Quais os valores utilizados pelos leitores de CD ?
– E pelos DATs ?
• Para sinal medindo a abertura e fecho das
cordas vocais ?
• Para sinal gravado via telefone ?
AT 2006
33
Representação de sinais digitais
• Depois da amostragem e quantização ficamos
com uma lista de números que facilmente se
podem tratar em programas como o SFS e o
Matlab
– As sinusóides que temos vindo a ver são de facto
listas de números como a seguinte:
•
AT 2006
0
0.0251
0.0502
0.0753
0.1004
0.1253
0.1502 0.1750
0.1997
0.2243 ....
34
Conversão D/A
AT 2006
35
Reconstrução com impulsos quadrados –
“hold”
AT 2006
36
Operações com sinais
AT 2006
37
Operações com sinais I
• Operações na variável dependente
– Mudança de escala (da amplitude)
• y(t)=c x(t) ou y[n]=c x[n]
• Exemplo: Amplificador electrónico
– Adição
• y(t)= x1(t) + x2(t)
• Exemplo: mixer áudio
– Multiplicação
• y(t)= x1(t) x2(t)
• Exemplo: sinal de rádio AM (modulação de Amplitude)
– Diferenciação, Integração
• Ex: bobine e condensador
AT 2006
38
Operações na variável independente
• Mudança da escala
temporal
x(t)
– y(t)= x (a t)
x(2t)
t
a>1 =>
compressão
0<a<1 => expansão
•Alguma ideia de aplicação na
área da fala?
AT 2006
t
x(t/2)
t
39
Operações na variável independente
x(t)
• inversão temporal
y(t)= x (- t)
-t1
t2
t
y(t)=x(-t)
-t2
AT 2006
t1
t
40
Som em Matlab
>> Ver Matlab num Instante
AT 2006
41
Sumário
• Geração de som com o Matlab
– Funções do Matlab para manipular sons
•sound/ soundsc
•wavread
•wavwrite
– Geração de sons artificais
•
•
•
•
AT 2006
ruído
sinusóides
soma de duas sinusóides
sinusóides de frequência variável
42
Som no Matlab
• É possível utilizar o Matlab na manipulação e
geração de som.
• Existem funções para ler ficheiros de som para
um vector, gravar um vector para um ficheiro e
para reproduzir sons a partir de ficheiros.
• Podem-se ouvir os vectores!
AT 2006
43
Função sound
A função sound permite reproduzir um som
armazenado num vector.
Sintaxe
sound(x,fa)
em que x é um vector linha ou coluna
e fa é a frequência de amostragem que se
pretende utilizar.
A função soundsc normaliza o vector para ter
máximo igual a 1.0
AT 2006
44
Função wavread
A função wavread lê um ficheiro de som em
formato “wav” do Windows.
Sintaxe
[x,fa,bits]= wavread(’ficheiro’)
em que x é um vector ,
fa é a frequência de amostragem utilizada
bits o número de bits
e ‘ficheiro’ é o ficheiro de som que se pretende
ler.
AT 2006
45
Função wavwrite
A função wavwrite escreve um ficheiro de
som em formato “wav” do Windows.
Sintaxe
wavwrite(x,fa,’ficheiro’)
em que x é um vector ,
fa é a frequência de amostragem utilizada
e ‘ficheiro’ é o ficheiro de som onde se pretende
guardar o som armazenado em x.
AT 2006
46
Exemplo: ficheiro de som
Neste exemplo pretende-se ler para um vector
um som armazenado num ficheiro e reproduzilo no Matlab
[x,fa]= wavread('som.wav');
sound(x,fa)
AT 2006
% ou soundsc(x,fa)
47
Exemplo: Gravar um som
• Neste exemplo lê-se para um vector
armazenado num ficheiro, manipula-se e
grava-se num ficheiro diferente.
[x,fa]= wavread('som.wav');
sound(x,fa)
y= x(end:-1:1);
% Inverte no tempo
wavwrite(y,fa,'som2.wav');
AT 2006
48
Alteração da freq. de amostragem
• Ao reproduzir um som é possível alterar a
frequência de amostragem com que é
reproduzido.
– Exemplo: utilizando o dobro da frequência de
amostragem do original.
•sound(x,fa*2)
– Exemplo: utilizando metade da frequência de
amostragem do original
•sound(x,fa/2)
AT 2006
49
Geração de sons artificiais
O Matlab possui formas expeditas de gerar sons
artificais. Vamos ver como é que se geram
diferentes tipos de sons.
A função rand gera uma sequência pseudo
aleatória. Qual será o som produzido por um
vector gerado com este função?
x= rand(1,10000)-0.5;
sound(x,8000);
AT 2006
% Ruído de média nula
50
Geração de sons artificiais
A função seno desempenha um papel central na
geração de sons articiais.
Vejamos qual o som que obtemos.
fa= 8000; Ta= 1/fa;
t= 0:Ta:1; %Gera o sinal de tempo
x= sin(2*pi*1000*t);
% sinusóide de 400Hz
sound(x,fa);
=2f
AT 2006
51
Geração de sons artificiais
Soma de duas sinusóides
Podemos gerar dois vectores com sinusóides
com frequências diferentes e somá-los para
ouvir o resultado
fa= 8000; Ta= 1/fa;
t= 0:Ta:1; %Gera o sinal de tempo
x= sin(2*pi*400*t);
% sinusóide de 400Hz
y= sin(2*pi*410*t);
% sinusóide de 410Hz
soundsc(x+y,fa);
AT 2006
52
Geração de sons artificiais
Multiplicação de sinusóides
Podemos gerar dois vectores com sinusóides de
frequências diferentes e realizar um produto
ponto-a-ponto entre eles.
fa= 8000; Ta= 1/fa;
t= 0:Ta:1; %Gera o sinal de tempo
x= sin(2*pi*400*t);
% sinusóide de 400Hz
y= sin(2*pi*80*t);
% sinusóide de 80Hz
soundsc(x.*y,fa);
AT 2006
53
Geração de sons artificiais
Sinusóides de frequência variável
Com o Matlab não é muito díficil gerar uma
sinusóide cuja frequência varia linearmente ao
longo do tempo.
fa= 8000; Ta= 1/fa;
t= [0:Ta:2 2:-Ta:0];
%Gera o
tempo
x= sin(2*pi*400*t.*t);
sound(x,fa)
AT 2006
54
Geração de sons artificiais
Sinusóides de frequência variável
Neste exemplo temos uma sinusóide cuja
frequência varia ao longo do tempo de forma
sinusóidal.
fa= 8000; Ta= 1/fa;
t= 0:Ta:2;
%Gera o sinal de tempo
s= 80*sin(2*pi*5*t);
x= sin(2*pi*400*t + s);
sound(x,fa)
AT 2006
55
TPC 
• Leitura dos 2 capítulos relativos a sinais do
livro Rosen & Howell
– disponíveis em forma digital
AT 2006
56