Aula nº 7 (27/10/2008, Sala 204-II) - Moodle @ FCT-UNL

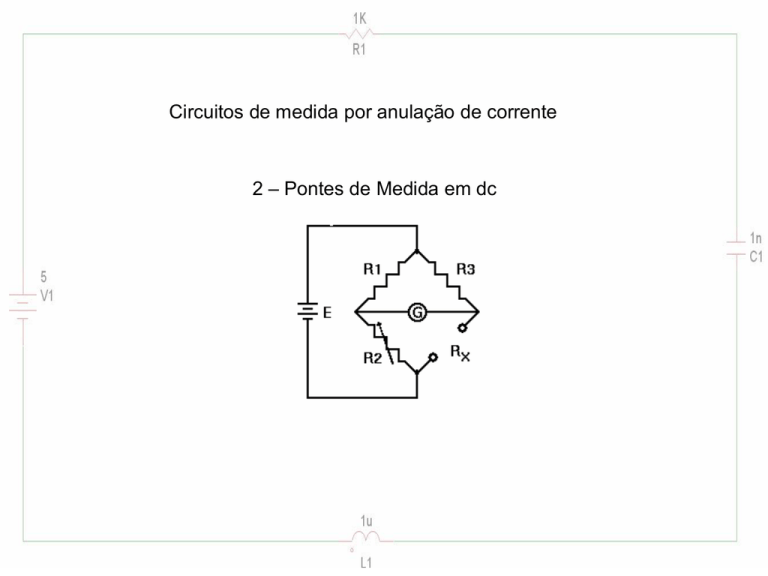
Circuitos de medida por anulação de corrente
2 – Pontes de Medida em dc
1 – Ponte de Wheatsone
A
R1
C
R2
D
G
Rx
R3
B
Se VAC = VAD então VCB = VDB e VCD = 0
Se VCB então IG =0
-> Princípio de banceamento ou de equilíbrio (corrente nula)
A
1 – Ponte de Wheatsone
R1
C
Nestas condições,
R2
D
G
Rx
R3
VAC = I(R1).R1 = VAD = I(R2).R2
B
VCB = I(R3).R3 = VDB = I(R4).R4
Mas, se IG = 0 então I(R1)=I(R3) e I(R2)=I(R4)
Então:
VAC I ( R1 ).R1 VAD I ( R2 ).R2



VCB I ( R1 ).R3 VDB I ( R2 ).R4
R
R
1
2
Desta
se conhecermos R1, R2 e R3
forma,
poderemos determinar R4
R
R
3
4
A
1 – Ponte de Wheatsone
R1
C
 Determinar Rx se:
R1 = 2 kW
R2 = 4 kW
R3 = 6 kW
IG = 0
R2
D
G
5V
Rx
R3
B
Rx = 12 kW
 Determinar Rx se:
R1 = 2 kW
R2 = 4 kW
R3 = 6 kW
RG = 50W
IG = 50 mA (sentido C->D)
Rx = 9,617 kW
1A – Loop de Varley
Subestação A
R1
Subestação B
R2
12V
G
R3
S
(1)
(2)
x
Com S →1, Rx corresponde à resistência dos cabos (ida e volta) que estão
entre a subestação A e a subestação B.
Com S → 2, Rx corresponde à resistência dos cabos da ida A-B e da volta
até ao ponto x.
R3 real corresponde à soma de R3 com a resistência entre x e a
subestação A
1A – Loop de Varley
Subestação A
R1
Subestação B
R2
12V
G
R3
S
x
(1)
(2)
Assim, Com S → 1 tem-se:
Com S → 2 tem-se
R1
R
 2
R3 RTotal
R1
R2

R3  RAX RTotal  RAX
Sabendo-se RAX e conhecendo-se as características do cabo (resistência por
unidade de comprimento) pode-se saber a que distância de A se encontra
o contacto ao solo.
Apêndice X
Teorema de Thévenin (versão dc)
Qualquer circuito contendo apenas fontes de tensão, fontes de corrente e
resistências, pode ser convertido (simplificado) num circuito composto apenas
por uma fonte de tensão e uma resistência em série.
Apêndice X
Teorema de Thévenin (versão dc)
Regras para a obtenção de Vth e Rth:
1 – Vth: Determinar a tensão entre A e B em circuito aberto (sem nenhum
componente externo a unir os pontos A e B.
2 – Rth: Determinar a resistência equivalente entre os pontos A e B,
curtocircuitando todas as fontes.
Apêndice X
Teorema de Thévenin (versão dc)
 Determinar o circuito equivalente de Thévenin de uma ponte de
Wheatstone, do ponto de vista dos terminais do galvanómetro (retirando o
galvanómetro).
 R3
R4 

Vth  Va  Vb  V 

 R1  R3 R2  R4 
R1
V
a
R3
Rth  R1 // R3  R2 // R4 
R1 R3
RR
 2 4
R1  R3 R2  R4
R2
b
Rx
Apêndice X
 R3
R4 

Vth  Va  Vb  V 

 R1  R3 R2  R4 
Teorema de Thévenin (versão dc)
Rth  R1 // R3  R2 // R4 
R1 R3
RR
 2 4
R1  R3 R2  R4
 Resolver o problema anterior da ponte não equilibrada recorrendo ao
teorema de Thévenin.
Determinar Rx se:
R1 = 2 kW
R2 = 4 kW
R3 = 6 kW
IG = 50 mA (sentido A->B)
Rm = 50W
R1
V
R2
a
b
5V
R3
Rx