Formulário: Velocidade média: Aceleração média: Equação horária

Colégio João e Rafaela Passalacqua
Colégio Santo Antonio de Lisboa
Colégio São Vicente de Paulo – Penha
Colégio Francisco Telles
Colégio São Vicente de Paulo – Jundiaí
Formulário:
Equação horária do espaço para M.U.V.:
Velocidade média:
Equação horária da velocidade para
M.U.V:
Aceleração média:
Equação horária para o Movimento Uniforme
(M.U.):
Equação de Torricelli para M.U.V.:
Unidades de medida no S.I.:
Velocidade média para dois trechos iguais:
Vm = 2.V1.V2 / (V1 + V2)
t–s
Conversão de unidade de velocidade:
Exercícios do livro – Física Básica – Nicolau/Toledo/Ronaldo
Capítulo
Página Inicial
Exercícios
1
10
V6 ao V13; A14,15,19; V16,18;
R10,13,20
2
28
V1 ao V4; A7,8,15; V5,8,15; R15
3
38
A3,13,14,16; V3,4,9,13,16,18, 22;
R5,22
6
76
V6 ao V9
24
336
A3 ao A5; V6,7, 9; R7
25
344
A1 ao A6; A9,10; V1,5,9,11; R9
Colégios Vicentinos – www.colegiosvicentinos.com.br
Colégio João e Rafaela Passalacqua
Colégio Santo Antonio de Lisboa
Colégio São Vicente de Paulo – Penha
Colégio Francisco Telles
Colégio São Vicente de Paulo – Jundiaí
Exercícios Gerais de Cinemática
I e Óptica I
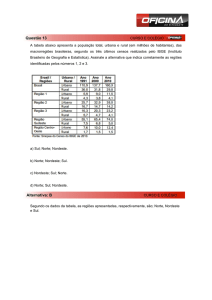
1. (Enem 2014) Um pesquisador avaliou o efeito da temperatura do motor (em velocidade constante) e
da velocidade média de um veículo (com temperatura do motor constante) sobre a emissão de monóxido
de carbono (CO) em dois tipos de percurso, aclive e declive, com iguais distâncias percorridas em linha
reta. Os resultados são apresentados nas duas figuras.
A partir dos resultados, a situação em que ocorre maior emissão de poluentes é aquela na qual o
percurso é feito com o motor
a) aquecido, em menores velocidades médias e em pista em declive.
b) aquecido, em maiores velocidades médias e em pista em aclive.
c) frio, em menores velocidades médias e em pista em declive.
d) frio, em menores velocidades médias e em pista em aclive.
e) frio, em maiores velocidades médias e em pista em aclive.
2. Drones são veículos voadores não tripulados, controlados remotamente e guiados por GPS. Uma de
suas potenciais aplicações é reduzir o tempo da prestação de primeiros socorros, levando pequenos
equipamentos e instruções ao local do socorro, para que qualquer pessoa administre os primeiros
cuidados até a chegada de uma ambulância. Considere um caso em que o drone ambulância se deslocou
9 km em 5 minutos. Nesse caso, o módulo de sua velocidade média é de aproximadamente
a) 1,4 m / s.
b) 30 m / s.
c) 45 m / s.
d) 140 m / s.
3. Em agosto deste ano realizou-se na China o campeonato mundial de atletismo, no qual um dos eventos
mais aguardados era a prova de 100 m masculino, que acabou sendo vencida pelo jamaicano Usain Bolt,
com o tempo de 9,79 s. O tempo do segundo colocado, o americano Justin Gatlin, foi de 9,80 s. A diferença
entre os dois atletas na chegada foi de aproximadamente:
a) 0,1mm.
b) 1mm.
c) 1 cm.
d) 10 cm.
e) 1 m.
4. O número de bactérias em uma cultura cresce de modo análogo ao deslocamento de uma partícula em
movimento uniformemente acelerado com velocidade inicial nula. Assim, pode-se afirmar que a taxa de
crescimento de bactérias comporta-se da mesma maneira que a velocidade de uma partícula. Admita um
experimento no qual foi medido o crescimento do número de bactérias em um meio adequado de cultura,
durante um determinado período de tempo. Ao fim das primeiras quatro horas do experimento, o
5
número de bactérias era igual a 8  10 . Após a primeira hora, a taxa de crescimento dessa amostra, em
número de bactérias por hora, foi igual a:
5
a) 1,0  10
5
b) 2,0  10
5
c) 4,0  10
5
d) 8,0  10
Colégios Vicentinos – www.colegiosvicentinos.com.br
Colégio João e Rafaela Passalacqua
Colégio Santo Antonio de Lisboa
Colégio São Vicente de Paulo – Penha
Colégio Francisco Telles
Colégio São Vicente de Paulo – Jundiaí
5. Um automóvel parte do repouso em uma via plana, onde desenvolve
movimento retilíneo uniformemente variado. Ao se deslocar 4,0 m a partir do ponto de repouso, ele
passa por uma placa sinalizadora de trânsito e, 4,0 s depois, passa por outra placa sinalizadora 12 m
adiante. Qual a aceleração desenvolvida pelo automóvel?
2
a) 0,50 m s .
2
b) 1,0 m s .
2
c) 1,5 m s .
2
d) 2,0 m s .
2
e) 3,0 m s .
6. (Enem PPL 2013) Conta-se que um curioso incidente aconteceu durante a Primeira Guerra Mundial.
Quando voava a uma altitude de dois mil metros, um piloto francês viu o que acreditava ser uma mosca
parada perto de sua face. Apanhando-a rapidamente, ficou surpreso ao verificar que se tratava de um
projétil alemão.
PERELMAN, J. Aprenda física brincando. São Paulo: Hemus, 1970.
O piloto consegue apanhar o projétil, pois
a) ele foi disparado em direção ao avião francês, freado pelo ar e parou justamente na frente do piloto.
b) o avião se movia no mesmo sentido que o dele, com velocidade visivelmente superior.
c) ele foi disparado para cima com velocidade constante, no instante em que o avião francês passou.
d) o avião se movia no sentido oposto ao dele, com velocidade de mesmo valor.
e) o avião se movia no mesmo sentido que o dele, com velocidade de mesmo valor.
7. Em uma pista de competição, quatro carrinhos elétricos, numerados de I a IV, são movimentados de
acordo com o gráfico v  t a seguir.
O carrinho que percorreu a maior distância em 4 segundos tem a seguinte numeração:
a) I
b) II
c) III
d) IV
8. Uma lebre e uma tartaruga decidem apostar uma corrida de 32 m. Exatamente às 12h, é dada a largada.
A lebre dispara na frente, com velocidade constante de 5,0 m s. A tartaruga “corre’’ com velocidade
constante de 4,0 m min, sem parar até o fim do percurso. A lebre, percebendo quão lenta se movia a
tartaruga, decide descansar após percorrer metade da distância total, e então adormece por 7min55s.
Quando acorda, sai correndo com a mesma velocidade inicial, para tentar ganhar a corrida. O fim da
história é conhecido. Qual é a vantagem de tempo da tartaruga sobre a lebre, na chegada, em segundos?
a) 1,4
b) 1,8
c) 3,2
d) 5,0
e) 6,4
Colégios Vicentinos – www.colegiosvicentinos.com.br
Colégio João e Rafaela Passalacqua
Colégio Santo Antonio de Lisboa
Colégio São Vicente de Paulo – Penha
Colégio Francisco Telles
Colégio São Vicente de Paulo – Jundiaí
9. Duas partículas, 1 e 2, se movem ao longo de uma linha horizontal, em rota
de encontro com velocidades iniciais de módulos iguais a v1  10m / s e v2  14 m / s e acelerações
2
2
contrárias às suas velocidades de módulos a1  1,0m / s e a2  0,5m / s .
Sabendo que o encontro entre elas ocorre, apenas, uma vez, o valor da separação inicial, d, entre as
partículas vale
a) 4 m
b) 8 m
c) 16 m
d) 96 m
e) 192 m
10. Um carro, partindo do repouso, desloca-se em um trecho A de modo que sua velocidade aumente
linearmente com o tempo até atingir 60km h. Após algum tempo, em um trecho B, o motorista aciona o
freio, de modo que a velocidade decresça também linearmente com o tempo. Considere que a trajetória
do automóvel é retilínea nos dois trechos e que ambos sejam estradas sem aclives ou declives. Assim,
pode-se afirmar corretamente que o vetor aceleração nos dois trechos tem
a) mesma direção e mesmo sentido.
b) mesma direção e sentido contrário.
c) mesmo módulo e mesmo sentido.
d) direções perpendiculares e mesmo módulo.
11. Considere o gráfico abaixo, que representa a velocidade de um corpo em movimento retilíneo em
função do tempo, e as afirmativas que seguem.
2
I. A aceleração do móvel é de 1,0 m / s .
II. A distância percorrida nos 10 s é de 50 m.
III. A velocidade varia uniformemente, e o móvel percorre 10 m a cada segundo.
IV. A aceleração é constante, e a velocidade aumenta 10 m / s a cada segundo.
São verdadeiras apenas as afirmativas
a) I e II.
b) I e III.
c) II e IV.
d) I, III e IV.
e) II, III e IV.
Colégios Vicentinos – www.colegiosvicentinos.com.br
Colégio João e Rafaela Passalacqua
Colégio Santo Antonio de Lisboa
Colégio São Vicente de Paulo – Penha
Colégio Francisco Telles
Colégio São Vicente de Paulo – Jundiaí
12. Um ponto material movimenta-se sobre uma trajetória retilínea. O gráfico
da posição em função do tempo do movimento é um arco de parábola, como indicado abaixo.
A equação horária que rege este movimento, segundo as informações fornecidas é
a) X  t
b) X  t  2
2
c) X  t
2
d) X  t  2t
13. Um corpo A é abandonado de um ponto situado a 10 metros acima do solo. No mesmo instante, um
corpo B é lançado verticalmente de baixo para cima com velocidade v 0 suficiente para que possa atingir
10 metros de altura.
Desprezando a resistência do ar, chamando respectivamente v A e vB as velocidades de A e B quando se
encontram a 5 metros de altura, o valor da razão v A vB , em módulo é
a) 4
b) 2
c) 1
d) 1 2
14. Uma ave marinha costuma mergulhar de uma altura de 20 m para buscar alimento no mar.
Suponha que um desses mergulhos tenha sido feito em sentido vertical, a partir do repouso e
exclusivamente sob ação da força da gravidade.
Desprezando-se as forças de atrito e de resistência do ar, a ave chegará à superfície do mar a uma
velocidade, em m/s, aproximadamente igual a:
a) 20
b) 40
c) 60
d) 80
Colégios Vicentinos – www.colegiosvicentinos.com.br
Colégio João e Rafaela Passalacqua
Colégio Santo Antonio de Lisboa
Colégio São Vicente de Paulo – Penha
Colégio Francisco Telles
Colégio São Vicente de Paulo – Jundiaí
TEXTO PARA A PRÓXIMA QUESTÃO:
Um objeto que não pode ser considerado uma partícula é solto de uma dada altura sobre um lago. O
gráfico ao lado apresenta a velocidade desse objeto em função do tempo. No tempo t = 1,0 s, o objeto toca
a superfície da água. Despreze somente a resistência no ar.
15. Qual a profundidade do lago?
a) 1 m
b) 5 m
c) 7 m
d) 100 m
e) 1000 m
16. A figura adiante mostra uma vista superior de dois espelhos planos montados verticalmente, um
perpendicular ao outro. Sobre o espelho OA incide um raio de luz horizontal, no plano do papel,
mostrado na figura. Após reflexão nos dois espelhos, o raio emerge formando um ângulo è com a normal
ao espelho OB. O ângulo è vale:
a) 0°
b) 10°
c) 20°
d) 30°
e) 40°
17. A figura a seguir representa um espelho plano, um objeto, O, sua imagem, I, e cinco observadores em
posições distintas, A, B, C, D e E.
Entre as posições indicadas, a única da qual o observador poderá ver a imagem I é a posição
a) A.
b) B.
c) C.
d) D.
e) E.
Colégios Vicentinos – www.colegiosvicentinos.com.br
Colégio João e Rafaela Passalacqua
Colégio Santo Antonio de Lisboa
Colégio São Vicente de Paulo – Penha
Colégio Francisco Telles
Colégio São Vicente de Paulo – Jundiaí
18. Maria, localizada no ponto M, observa a imagem de Joana, que está em J,
através de um espelho plano vertical E fixo a uma parede. O esquema indica as dimensões do ambiente e
a largura do espelho.
Maria vai se locomover em um só sentido, paralelamente ao espelho, sem perder a imagem de Joana.
Pelas dimensões indicadas no esquema, o maior deslocamento que Maria pode realizar, em metros, é
igual a
a) 5,0
b) 4,0
c) 3,5
d) 3,0
e) 2,5
19. Uma câmara escura de orifício fornece a imagem de um prédio, o qual se apresenta com altura de 5
cm. Aumentando-se de 100 m a distância do prédio à câmara, a imagem se reduz para 4 cm de altura.
Qual é a distância entre o prédio e a câmara, na primeira posição?
a) 100 m
b) 200 m
c) 300 m
d) 400 m
e) 500 m
20. No mundo artístico as antigas "câmaras escuras" voltaram à moda. Uma câmara escura é uma caixa
fechada de paredes opacas que possui um orifício em uma de suas faces. Na face oposta à do orifício fica
preso um filme fotográfico, onde se formam as imagens dos objetos localizados no exterior da caixa,
como mostra a figura.
Suponha que um objeto de 3m de altura esteja a uma distância de 5m do orifício, e que a distância entre
as faces seja de 6cm.
Calcule a altura h da imagem.
21. (Enem cancelado 2009) No mundial de 2007, o americano Bernard Lagat, usando pela primeira vez
uma sapatilha 34% mais leve do que a média, conquistou o ouro na corrida de 1.500 metros com um
tempo de 3,58 minutos. No ano anterior, em 2006, ele havia ganhado medalha de ouro com um tempo de
3,65 minutos nos mesmos 1.500 metros. Revista Veja, São Paulo, ago. 2008 (adaptado).
Sendo assim, a velocidade média do atleta aumentou em aproximadamente
a) 1,05%.
b) 2,00%.
c) 4,11%.
d) 4,19%. e) 7,00%.
Colégios Vicentinos – www.colegiosvicentinos.com.br
Colégio João e Rafaela Passalacqua
Colégio Santo Antonio de Lisboa
Colégio São Vicente de Paulo – Penha
Colégio Francisco Telles
Colégio São Vicente de Paulo – Jundiaí
22. (Enem cancelado 2009) O Super-homem e as leis do movimento
Uma das razões para pensar sobre física dos super-heróis é, acima de tudo, uma forma divertida de
explorar muitos fenômenos físicos interessantes, desde fenômenos corriqueiros até eventos
considerados fantásticos. A figura seguinte mostra o Super-homem lançando-se no espaço para chegar ao
topo de um prédio de altura H. Seria possível admitir que com seus superpoderes ele estaria voando com
propulsão própria, mas considere que ele tenha dado um forte salto. Neste caso, sua velocidade final no
ponto mais alto do salto deve ser zero, caso contrário, ele continuaria subindo. Sendo g a aceleração da
gravidade, a relação entre a velocidade inicial do Super-homem e a altura atingida é dada por: v2 = 2gH.
A altura que o Super-homem alcança em seu salto depende do quadrado de sua velocidade inicial porque
a) a altura do seu pulo é proporcional à sua velocidade média multiplicada pelo tempo que ele
permanece no ar ao quadrado.
b) o tempo que ele permanece no ar é diretamente proporcional à aceleração da gravidade e essa é
diretamente proporcional à velocidade.
c) o tempo que ele permanece no ar é inversamente proporcional à aceleração da gravidade e essa é
inversamente proporcional à velocidade média.
d) a aceleração do movimento deve ser elevada ao quadrado, pois existem duas acelerações envolvidas: a
aceleração da gravidade e a aceleração do salto.
e) a altura do seu pulo é proporcional à sua velocidade média multiplicada pelo tempo que ele
permanece no ar, e esse tempo também depende da sua velocidade inicial.
23. (Enem 2014) As lentes fotocromáticas escurecem quando expostas à luz solar por causa de reações
químicas reversíveis entre uma espécie incolor e outra colorida. Diversas reações podem ser utilizadas, e
a escolha do melhor reagente para esse fim se baseia em três principais aspectos: (i) o quanto escurece a
lente; (ii) o tempo de escurecimento quando exposta à luz solar; e (iii) o tempo de esmaecimento em
ambiente sem forte luz solar. A transmitância indica a razão entre a quantidade de luz que atravessa o
meio e a quantidade de luz que incide sobre ele.
Durante um teste de controle para o desenvolvimento de novas lentes fotocromáticas, foram analisadas
cinco amostras, que utilizam reagentes químicos diferentes. No quadro, são apresentados os resultados.
Transmitância
Tempo de
Tempo de
média da lente
Amostra escurecimento esmaecimento
quando exposta à
(segundo)
(segundo)
luz solar (%)
Colégios Vicentinos – www.colegiosvicentinos.com.br
Colégio João e Rafaela Passalacqua
Colégio Santo Antonio de Lisboa
Colégio São Vicente de Paulo – Penha
Colégio Francisco Telles
Colégio São Vicente de Paulo – Jundiaí
1
2
3
4
5
20
40
20
50
40
50
30
30
50
20
80
90
50
50
95
Considerando os três aspectos, qual é a melhor amostra de lente fotocromática para se utilizar em
óculos?
a) 1
b) 2
c) 3
d) 4
e) 5
24. (Enem 2ª aplicação 2010)
Os quadrinhos mostram, por meio da projeção da sombra da árvore e do menino, a sequência de
períodos do dia: matutino, meio-dia e vespertino, que é determinada
a) pela posição vertical da árvore e do menino.
b) pela posição do menino em relação à árvore.
c) pelo movimento aparente do Sol em torno da Terra.
d) pelo fuso horário específico de cada ponto da superfície da Terra.
e) pela estação do ano, sendo que no inverno os dias são mais curtos que no verão.
25. (Unicamp 2015) A Agência Espacial Brasileira está desenvolvendo um veículo lançador de satélites
(VLS) com a finalidade de colocar satélites em órbita ao redor da Terra. A agência pretende lançar o VLS
em 2016, a partir do Centro de Lançamento de Alcântara, no Maranhão.
a) Considere que, durante um lançamento, o VLS percorre uma distância de 1200km em 800s. Qual é a
velocidade média do VLS nesse trecho?
b) Suponha que no primeiro estágio do lançamento o VLS suba a partir do repouso com aceleração
resultante constante de módulo aR . Considerando que o primeiro estágio dura 80s, e que o VLS percorre
uma distância de 32km, calcule aR .
TEXTO PARA AS PRÓXIMAS 2 QUESTÕES:
Recentemente, uma equipe de astrônomos afirmou ter identificado uma estrela com dimensões
comparáveis às da Terra, composta predominantemente de diamante. Por ser muito frio, o astro,
possivelmente uma estrela anã branca, teria tido o carbono de sua composição cristalizado em forma de
um diamante praticamente do tamanho da Terra.
Colégios Vicentinos – www.colegiosvicentinos.com.br
Colégio João e Rafaela Passalacqua
Colégio Santo Antonio de Lisboa
Colégio São Vicente de Paulo – Penha
Colégio Francisco Telles
Colégio São Vicente de Paulo – Jundiaí
18
26. (Unicamp 2015) Os astrônomos estimam que a estrela estaria situada a uma distância d  9,0  10 m
4
da Terra. Considerando um foguete que se desloca a uma velocidade v  1,5  10 m / s, o tempo de viagem
do foguete da Terra até essa estrela seria de
(1ano  3,0  107 s)
a) 2.000 anos.
b) 300.000 anos.
c) 6.000.000 anos.
d) 20.000.000 anos.
27. (Unicamp 2015) Considerando que a massa e as dimensões dessa estrela são comparáveis às da
Terra, espera-se que a aceleração da gravidade que atua em corpos próximos à superfície de ambos os
astros seja constante e de valor não muito diferente. Suponha que um corpo abandonado, a partir do
repouso, de uma altura h  54 m da superfície da estrela, apresente um tempo de queda t  3,0 s. Desta
forma, pode-se afirmar que a aceleração da gravidade na estrela é de
2
a) 8,0 m / s .
2
b) 10 m / s .
2
c) 12 m / s .
2
d) 18 m / s .
28. (Unicamp 2014) Correr uma maratona requer preparo físico e determinação. A uma pessoa comum
se recomenda, para o treino de um dia, repetir 8 vezes a seguinte sequência: correr a distância de 1 km à
velocidade de 10,8 km/h e, posteriormente, andar rápido a 7,2 km/h durante dois minutos.
a) Qual será a distância total percorrida pelo atleta ao terminar o treino?
b) Para atingir a velocidade de 10,8 km/h, partindo do repouso, o atleta percorre 3 m com aceleração
constante. Calcule o módulo da aceleração a do corredor neste trecho.
Colégios Vicentinos – www.colegiosvicentinos.com.br
Colégio João e Rafaela Passalacqua
Colégio Santo Antonio de Lisboa
Colégio São Vicente de Paulo – Penha
Colégio Francisco Telles
Colégio São Vicente de Paulo – Jundiaí
Gabarito dos exercícios Gerais:
Resposta da questão 1: [D]
A primeira figura nos permite concluir que para menores temperaturas (motor frio) e em pista em aclive
a emissão de CO é maior.
A segunda figura mostra que a emissão de CO é maior para baixas velocidades médias e em pista em
aclive.
Resposta da questão 2: [B]
Observação: rigorosamente, o enunciado deveria especificar tratar-se do módulo da velocidade escalar
média.
Dados : ΔS  9 km  9.000 m; Δt  5 min  300 s.
vm 
ΔS 9.000

Δt
300

vm  30 m/s.
Resposta da questão 3: [D]
Utilizando as informações dadas no enunciado, podemos calcular as velocidades médias dos dois
corredores, sendo elas:
v1 
ΔS 100

Δt1 9,79
v2 
ΔS 100

Δt 2 9,80
10,21m s
10,20 m s
Desta forma, a velocidade relativa entre os corredores pode ser calculada.
vR  v1  v 2  10,21  10,20
vR  0,01m s
Assim, a distância entre os atletas (Δx) é dada pela multiplicação da velocidade relativa pelo tempo que o
competidor que chega primeiro (Usain Bolt) chega a linha de chegada. Assim,
Δx  vR  t1
Δx  0,01 9,79
Δx 10 cm
Resposta da questão 4:[A]
O deslocamento (ΔS) de uma partícula em movimento uniformemente variado a partir do repouso e a
velocidade v são:

a 2
ΔS  t
2

v  a t

sendo a a aceleração escalar e t o tempo de movimento.
Colégios Vicentinos – www.colegiosvicentinos.com.br
Colégio João e Rafaela Passalacqua
Colégio Santo Antonio de Lisboa
Colégio São Vicente de Paulo – Penha
Colégio Francisco Telles
Colégio São Vicente de Paulo – Jundiaí
Fazendo a analogia que sugere o enunciado e aplicando para o instantes t  4 h e t  1h, temos:
ΔN 
a 2
t
2
 8  105 
a
bactérias
2
4   a  1 105
.

2
h2
N  a t  N  1 105 1 
N  1 105
bactérias
.
h
Resposta da questão 5: [A]
Analisando o movimento do automóvel conforme a figura abaixo, temos que:
 v1

1 t1  t
 ΔS  4 m
 1
v 2

2 t2  t  4
 ΔS  16 m
 1
Assim, podemos encontrar expressões matemáticas que representam as velocidades nos dois instantes.
Analisando do instante 0 ao instante 1, temos que:
v12  v 02  2  a  ΔS1
v1  2  a  ΔS1
Analisando do instante 0 ao instante 2, temos que:
v 22  v 02  2  a  ΔS2
v 2  2  a  ΔS 2
Se v 2  v1  a  Δt , onde Δt  t2  t1  4 s .
2  a  ΔS2  2  a  ΔS1  a  Δt
a  Δt  2  a  ΔS2  2  a  ΔS1
a  Δt  2  a 

ΔS2  ΔS1

Elevando ao quadrado ambos os lados e substituindo os valores, temos que:
a 2  42  2  a 

4  16
16  a  2   2  4 
a

2
2
8
16
a  0,5 m s2
Resposta da questão 6: [E]
Colégios Vicentinos – www.colegiosvicentinos.com.br
Colégio João e Rafaela Passalacqua
Colégio Santo Antonio de Lisboa
Colégio São Vicente de Paulo – Penha
Colégio Francisco Telles
Colégio São Vicente de Paulo – Jundiaí
A velocidade do projétil em relação ao piloto era nula porque seus movimentos tinham mesmo sentido,
com velocidades de mesmo módulo.
Resposta da questão 7: [B]
No gráfico v  t, a distância percorrida é obtida pela ”área" entre a linha do gráfico e o eixo dos tempos.
Calculando cada uma delas:

 2  0,5 1
2  0,5

 1 2  0,5  1,25  2  3,75 m.
DI 
2
2





1,5  1 2
1 1

 1,5  1  0,5  2,5  1,5  4,5 m.
DII 
2
2





2 1
 2  1  1  2  3 m.
DIII 
2





D  3  0,5   0,5  11  0,75  0,75  1,5 m.
 IV
2
2
Resposta da questão 8: [A]
Calculando os tempos totais para cada competidor, em segundos, temos:
Para a tartaruga:
tT 
32 m
60 s
 8 min 
 480 s
4 m / min
1 min
Para a lebre:
tL 
2  16 m
60 s
 7 min 
 55 s  6,4 s  420 s  55 s  481,4 s
5 m/s
1 min
Logo, a diferença de tempo total pró-tartaruga é de:
tT  tL  481,4  480  1,4 s
Resposta da questão 9: [E]
Tomando as equações horárias das posições de cada móvel, temos:
s1  0  10t 
1 2
1
t
s2  d  14t  t 2
2
4
e
Colégios Vicentinos – www.colegiosvicentinos.com.br
Colégio João e Rafaela Passalacqua
Colégio Santo Antonio de Lisboa
Colégio São Vicente de Paulo – Penha
Colégio Francisco Telles
Colégio São Vicente de Paulo – Jundiaí
Em que S  posição de cada móvel (m) no instante t (s)
No encontro dos móveis, as posições são iguais. s1  s2
10t 
1 2
1
t  d  14t  t 2
2
4
Rearranjando os termos
3t 2  96t  4d  0
(1)
Sabendo que o encontro ocorre apenas uma vez, temos um choque totalmente inelástico, isto é, a
velocidade final das duas partículas é a mesma.
t
v1  10  t e v 2  14  2
v1  v 2
10  t  14 
t
48
t
 t  16 s
2
3
Substituindo o tempo encontrado na equação (1), obtemos:
3  162  96  16  4d  0  d  192m
Outra forma de pensar a resolução desta questão a partir da equação (1) é que o encontro dos móveis
significa as raízes da equação quadrática. Como esse encontro se dá uma única vez, temos duas raízes
reais iguais, ou seja, Δ  0, então:
( 96)2  4  3  4d  0
9216  48d  0
9216
d
 d  192 m
48
Resposta da questão 10: [B]
No trecho A, o carro parte do repouso e aumenta sua velocidade uniformemente até atingir a velocidade
de 60km h.
Desta forma, a aceleração durante o trecho A tem direção como sendo a horizontal e sentido da esquerda
para a direita.
No trecho B, o carro está inicialmente com uma velocidade de 60km h e vai desacelerando até atingir o
repouso.
Colégios Vicentinos – www.colegiosvicentinos.com.br
Colégio João e Rafaela Passalacqua
Colégio Santo Antonio de Lisboa
Colégio São Vicente de Paulo – Penha
Colégio Francisco Telles
Colégio São Vicente de Paulo – Jundiaí
Assim, a aceleração no trecho B tem mesma direção que no sentido A (horizontal), porém está no sentido
contrário (da direita para a esquerda).
Resposta da questão 11: [A]
[I] Verdadeira. Aplicando a definição de aceleração escalar média:
a  am 
Δv 10

 a  1 m/s2.
Δt 10
[II] Verdadeira. O espaço percorrido é dado pela área entre a linha do gráfico e o eixo dos tempos.
ΔS 
10  10
 ΔS  50 m.
2
[III] Falsa. A velocidade é variável.
[IV] Falsa. A velocidade aumenta 1,0 m/s a cada segundo.
Resposta da questão 12: [D]
Da equação horária das posições no MUV:
x(t) 
a 2
t  v 0 t  x0
2
Sendo assim, temos uma equação do 2º grau representada pela parábola no gráfico, e impossibilita as
alternativas [A] e [B] de serem as respostas, pois se tratam de retas.
Por outro lado, a inclinação da curva ao tocar o eixo vertical x, é dada pela tangente neste ponto de
encontro, que fisicamente falando, representa a velocidade inicial do móvel, sendo diferente de zero há
inclinação para cima  v0  0 ou para baixo  v0  0 que é o nosso caso. (Elimina-se, com isso, a alternativa
[C] e a resposta correta é a da alternativa [D].
Outra forma de pensar é extrair os valores do gráfico e substituir na equação formando um sistema de
equações:
Em
t  0 s, x0  0 m;

t  2 s, x  0 m;
t  3 s, x  3 m

Substituindo os valores dos pontos, temos:
x(2 s)  2a  2v0  2(a  v0 )  0  a  v0  0
(1)
Colégios Vicentinos – www.colegiosvicentinos.com.br
Colégio João e Rafaela Passalacqua
Colégio Santo Antonio de Lisboa
Colégio São Vicente de Paulo – Penha
Colégio Francisco Telles
Colégio São Vicente de Paulo – Jundiaí
x(3 s) 
9
3a
3a
a  3v 0  3(  v 0 )  3 
 v0  1
2
2
2
(2)
Fazendo (2) – (1):
a
 1 a  2 m / s2
2
e v0  2 m / s
Finalmente, substituindo os valores na equação de origem ficamos com:
x(t)  t 2  2t
Resposta da questão 13: [C]
Temos situações semelhantes para os dois corpos, pois ambos percorrem 5 m com as mesmas
acelerações sendo que as condições de contorno também são similares, logo as velocidades em módulo
serão iguais e sua razão será 1.
Outra possibilidade é calcular usando os conhecimentos de lançamento vertical e queda livre.
Para o corpo A, que cai em queda livre, usando o referencial positivo para baixo e a equação de Torricelli:
v 2  v02  2gΔh  v  v02  2gΔh
v A  02  2  10  5  v  10 m / s
Para o corpo B, que sobe na vertical, usando o referencial positivo para cima, primeiramente
descobrimos a velocidade inicial e depois a velocidade na posição de 5 m :
v2  v02  2gΔh  v0  v2  2gΔh
v0  02  2  10  10  v0  10 2 m s
E a intensidade da velocidade a 5 m de altura:
vB 
10 2 
Então,
2
 2  10  5  v  10 m / s
v A 10

 1.
vB 10
Resposta da questão 14: [A]
Usando a equação de Torricelli com a = g = 10 m/s2 e ΔS  h  20m.
v 2  v 02  2g h  v 2  0  2  10  20  400 
v  20 m/s.
Colégios Vicentinos – www.colegiosvicentinos.com.br
Colégio João e Rafaela Passalacqua
Colégio Santo Antonio de Lisboa
Colégio São Vicente de Paulo – Penha
Colégio Francisco Telles
Colégio São Vicente de Paulo – Jundiaí
Resposta da questão 15: [C]
Pela leitura do gráfico, conclui-se que o objeto atinge a superfície do lago no instante t = 1 s, com
velocidade de 10 m/s, pois a partir desse instante sua velocidade começa a diminuir, chegando ao fundo
do lago no instante t = 3,5 s, quando a velocidade se anula.
A profundidade do lago (h2) pode ser calculada pela “área” (A2) da figura abaixo da linha do gráfico entre
t = 1 s a t = 3,5 s.
h2  " A 2 " 
1 9
  3,5  1  1  4,5  2,5 
2
h2  7 m.
Resposta da questão 16:[C]
Resposta da questão 17:[B]
Resposta da questão 18:[E]
Resposta da questão 19: [D]
Resposta da questão 20:
Por semelhança de triângulos:
h 3
18

 h

6 5
5
h  3,6 cm.
Resposta da questão 21: [B]
Dados: d = 1.500 m; t1 = 3,65 min; t2 = 3,58 min.
v1 
d
t1
e
v2
d t
  1
v1 t 2 d
v2 
d
t2
. Dividindo membro a membro:
v 2 t1 3,65
 
v1 t 2 3,58
v2
 1,02
v1
v2 
102
v1
100



 v2 = 102% v1.
Portanto, houve um aumento de, aproximadamente, 2,00% na velocidade média.
Colégios Vicentinos – www.colegiosvicentinos.com.br
Colégio João e Rafaela Passalacqua
Colégio Santo Antonio de Lisboa
Colégio São Vicente de Paulo – Penha
Colégio Francisco Telles
Colégio São Vicente de Paulo – Jundiaí
Resposta da questão 22: [E]
Desprezando os efeitos do ar e orientando a trajetória para cima, a aceleração do Super-homem é a = – g.
O gráfico da velocidade em função do tempo até o ponto mais alto está dado abaixo.
A área hachurada é numericamente igual a ao espaço
percorrido pelo super-homem, no caso, a altura H.
Assim:
v
t
H =”Área” = 2 .
v
Mas 2 é a velocidade média, vm.
Então: H = vm t.
A equação da velocidade na subida é:
v' = v – g t. Como no ponto mais alto a velocidade se
anula, temos:
0 = v – gt 
Assim:
t
v
g
.
v
g
H = vm t  H = vm .
Ou seja, a altura atingida é proporcional à sua
velocidade média multiplicada pelo tempo que ele
permanece no ar, e esse tempo também da sua
velocidade inicial.
Finalizando:
H=
 v  v 
 2  g 
  
 v2 = 2 g H.
Resposta da questão 23: [C]
A melhor amostra é aquela que melhor concilia o menor tempo de escurecimento, menor tempo de
esmaecimento e menor transmitância.
Resposta da questão 24: [C]
A sombra projetada é determinada pela posição do Sol relativamente à Terra.
Resposta da questão 25:
3
a) Dados: ΔS  1.200 km  1.200  10 m; Δt  800 s.
vm 
ΔS 1.200  103


Δt
800
vm  1.500 m/s.
b) Dados: S  32 km  32.000 m; S0  0; v0  0; t  80 s.
Colégios Vicentinos – www.colegiosvicentinos.com.br
Colégio João e Rafaela Passalacqua
Colégio Santo Antonio de Lisboa
Colégio São Vicente de Paulo – Penha
Colégio Francisco Telles
Colégio São Vicente de Paulo – Jundiaí
S  S0  v 0 t 
aR
2
t 2  32.000 
aR
2
802 
a R  10 m/s2.
Resposta da questão 26: [D]
Δt 
d
9  108
6  1014 s

 6  1014 s 
 2  107 anos 
7
v 1,5  104
3  10 s/ano
Δt  20.000.000 anos.
Resposta da questão 27: [C]
h
2 h 2  54
g 2
t  g


2
t2
32
g  12 m/s2.
Resposta da questão 28:
a) Dados: d1 = 1 km = 1.000 m; v2 = 7,2 km/h = 2 m/s; Δt2  2min  120s.
A distância total (d) percorrida nas 8 vezes é:


d  8  d1  d2   8 d1  v 2 Δt 2  8 1.000  2  120   8 1.240  
d  9.920 m.
b) Dados: v0 = 0; v1 = 10,8 km/h = 3 m/s; ΔS  3m.
Aplicando a equação de Torricelli:
v12  v 02  2 a ΔS  a 
v12  v 02 32  0 9


2 Δs
23
6

a  1,5 m/s2 .
Colégios Vicentinos – www.colegiosvicentinos.com.br