5. Fontes do campo magnético

5. Fontes do campo magnético: campo magnético criado por uma corrente
num condutor (lei de Biot-Savart, lei Ampère), magnetismo na matéria.
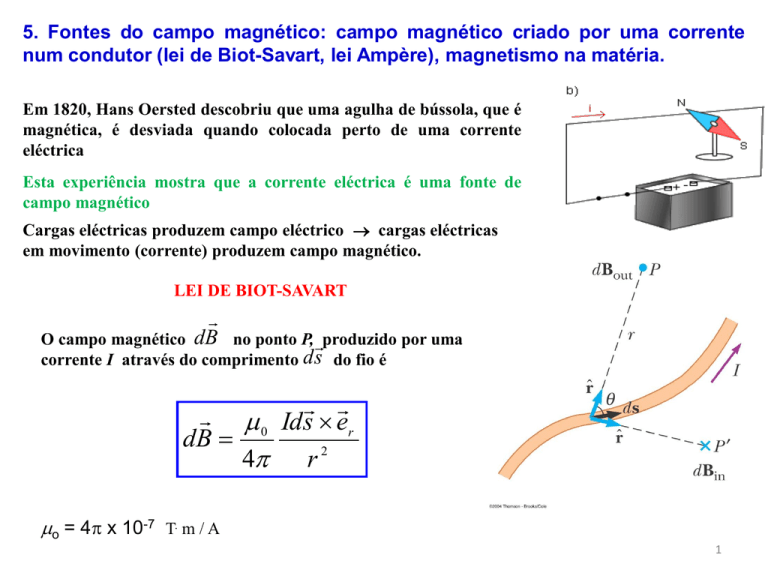
Em 1820, Hans Oersted descobriu que uma agulha de bússola, que é
magnética, é desviada quando colocada perto de uma corrente
eléctrica
Esta experiência mostra que a corrente eléctrica é uma fonte de
campo magnético
Cargas eléctricas produzem campo eléctrico  cargas eléctricas
em movimento (corrente) produzem campo magnético.
LEI DE BIOT-SAVART

dB
O campo magnético
no ponto P, produzido por uma
corrente I através do comprimento d s do fio é
  0 Ids  er
dB 
4
r2
o = 4 x 10-7 T. m / A
1
O campo magnético total será

 0 I
B   dB 
4
 
ds  er
 r2
Regra da mão direita para determinar a direcção
do campo magnético

Em volta de um fio longo transportando uma
corrente, as linhas do campo magnético formam
círculos em torno do fio.
Módulo do campo magnético
gerado pelo fio

B

B

B
0 I
B
2r
Linhas de campo magnético
ao redor do fio com corrente I
evidenciadas com limalhas de
ferro 
2
Em volta de um fio longo transportando uma corrente, as linhas do campo magnético formam
círculos em torno do fio.
3
FORÇA MAGNÉTICA ENTRE DOIS CONDUTORES PARALELOS

A corrente do fio 2 gera um campo magnético B2 na
posição do fio 1. B2 é perpendicular ao fio 1.
 correntes de mesmo sentido
A força magnética sobre o fio 1 é

 
F1  I1   B2
F1  I1B2
mas B2 
F1  I1(
F1 
0 I 2

2a
0 I 2
) ou
2a
 0 I 1 I 2
2a
Em termos de força magnética por unidade de comprimento
F1  0 I 1 I 2


2a
 Esta equação pode ser aplicada também a um fio de comprimento infinito
4


Supor agora que a corrente do fio 1 gera um campo magnético B na posição do fio 2. B1 é
1
perpendicular ao fio 1.

 
F2  I 2   B1
 0 I 1 I 2
 F2 
2a


 F2  F1
Os fios se atraem
Quando as correntes estão em direcções opostas, as forças magnéticas têm sentidos opostos e
os fios se repelem
Correntes na mesma direcção se atraem
Correntes em direcções opostas se repelem
5
A expressão
F1  0 I 1 I 2


2a
é utilizada para definir o Ampère:
Definição do Coulomb
6
LEI DE AMPÈRE
Com a lei de Gauss, que é uma
relação entre a carga eléctrica e o
campo eléctrico produzido por esta
carga, podíamos determinar o
campo eléctrico em situações
altamente simétricas .
Agora estudaremos a lei de
Ampère, que é uma relação
análoga no magnetismo  só
que é uma relação entre uma
corrente e o campo magnético
que esta corrente produz.
(a) A bússola aponta sempre
na mesma direcção  norte
geográfico)
(b) a bússola

direcção de B
aponta
na
 
Calculamos o produto B  ds para um pequeno
 segmento de comprimento
ds sobre a trajectória circular da Figura b. B  ds  Bds
B é constante e a soma dos produtos
 Bds
 sobre toda a trajectória
fechada  a integral de linha de B  ds :
 
0 I
B

d
s

B
ds


 2r (2r )   0 I
Para qualquer trajectória temos
 Lei Ampère
 
 B  ds   0 I
7
Exemplo 1: Cálculo do campo magnético criado por um fio longo que conduz uma corrente
rR
Trajectória circular 1
 
 B  ds  B  ds 
I0
B(2r )  0 I 0 
B
r<R
0 I 0
2r
Trajectória circular 2
r
I  I0
I
r 2
r 2
r2

 I
I0  2 I0
2
2
I 0 R
R
R
 
2

r
B

d
s

B
ds

B
(
2

r
)


I

0
0


I0
2
R
ou B 2r 
0 r 2
R
2
I0
0 I 0
 B
r
2
2R
8