Momento Angular

MOVIMENTO DE UM CORPO RÍGIDO
Um corpo rígido pode ter três movimentos
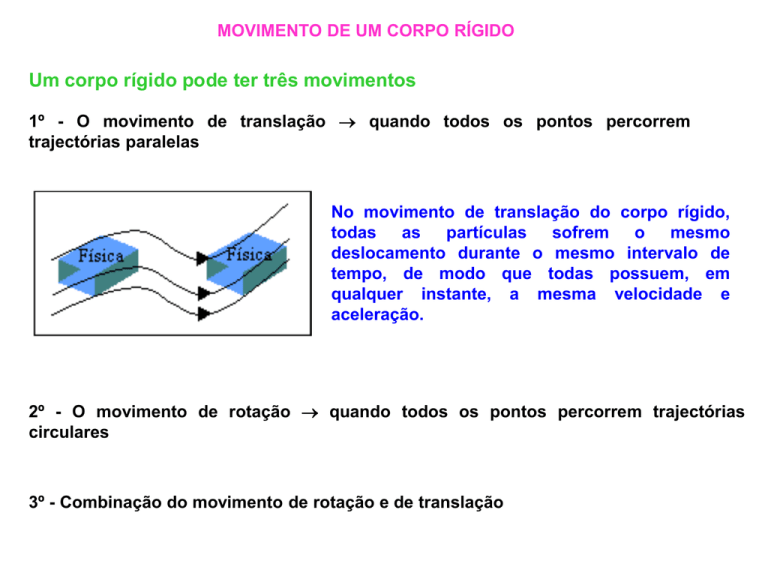
1º - O movimento de translação  quando todos os pontos percorrem
trajectórias paralelas
No movimento de translação do corpo rígido,
todas as partículas sofrem o mesmo
deslocamento durante o mesmo intervalo de
tempo, de modo que todas possuem, em
qualquer instante, a mesma velocidade e
aceleração.
2º - O movimento de rotação  quando todos os pontos percorrem trajectórias
circulares
3º - Combinação do movimento de rotação e de translação
 Movimento rotacional puro
 Movimento translacional + rotacional
MOVIMENTO DE ROTAÇÃO E TRANSLAÇÃO DA TERRA
ENERGIA CINÉTICA ROTACIONAL
Suponhamos um corpo rígido que gira ao redor de um eixo z
Cada partícula de massa mi do corpo rígido descreve uma
trajectória circular de raio ri com velocidade tangencial vi
Energia cinética de uma partícula do corpo rígido
1
K i  mi vi2
2
Relação entre a velocidade tangencial e velocidade angular
vi  ri
Substituindo em
Ki 
Ki
1
1
mi 2 ri 2  mi ri 2  2
2
2
Energia cinética total 
1

K total    mi ri 2  2
2 i

Não é uma nova forma de energia.
A forma é diferente porque é aplicada a um corpo em rotação
Unidade: joule (J)
MOMENTO DE INÉRCIA
1
K R  I 2
2
I   mi ri 2
onde
é o momento de inércia
i
Unidade : kg m 2
O momento de inércia representa uma resistência ao movimento de rotação
No movimento rotacional o momento de inércia exerce o mesmo papel que a massa
no movimento translacional
Podemos reescrever a expressão do momento de inércia em termos de dm
lim
2
2
I  mi 
r

m

r
0 i
i
 dm
i
MOMENTO DE INÉRCIA DE ALGUNS CORPOS RÍGIDOS
O MOMENTO ANGULAR
Definimos inicialmente o momento
 angular
partícula com momento linear p .
  
L r p

L

é o momento angular instantâneo L
de uma
  
L r p
em
relação à origem O

p
 m
r
Note que a partícula não precisa estar girando em
torno de O para ter momento angular em relação a este
ponto  a rotação não é necessária para o momento
angular
MOSTRAREMOS QUE O MOVIMENTO ROTACIONAL TEM UMA LEI DE MOVIMENTO
SEMELHANTE À SEGUNDA LEI DE NEWTON
Derivando o momento angular

L
em relação ao tempo:



dL d  
dr   dp
 (r  p) 
 p  r
dt dt
dt
dt
=0
como


f 

dp
dt


dL  
 r f  M
dt
ou

 dL
M
dt
análogo à segunda lei de newton
A relação acima é válida também para um sistema
de partículas onde o momento angular é a soma
vectorial dos momentos angulares de cada partícula
 em relação ao mesmo ponto fixo O
A mesma relação é válida para um corpo
rígido, em rotação em torno de um ponto O.

 dL
M
dt
A soma dos momentos das forças internos são nulos
e

M
corresponde à um momento da força externo resultante

 dp
f 
dt
O MOMENTO ANGULAR DE UM CORPO RÍGIDO
Suponhamos um corpo rígido que gira ao redor de um eixo z
Lembrando que
  
L r p
O momento angular total do corpo rígido será
L
m v r
i
i i
i
como vi  ri obtemos
L
2
m
(

r
)
r

(
m
r
 i i i  i i )
i
e
I 
i
2
m
r
 ii
é o momento de inércia
e o momento angular pode ser escrito como
que é análogo à
L  I
p  mv
O momento de inércia representa uma resistência ao movimento de rotação
CONSERVAÇÃO DO MOMENTO ANGULAR
Quando

 dL  

M
 r  f  0  L  constante
dt


se
i) f  0 ou ii) r  0

M 0
ou

L  constante


Li  L f
Análogo ao que acontece com o momento linear
 
pi  p f
iii) quando a força é colinear com o vector posição teremos também

M 0
Exemplo:
FORÇAS CENTRAIS, que são forças da forma
 

F (r )  f (r ) u
Neste caso:

 dL 

M
 r  f (r )u  0
dt

 L  constante
EXEMPLO 1: CONSERVAÇÃO DO MOMENTO ANGULAR
No sistema homem - halteres só há forças internas e, portanto:
L  I  constante

f I f
i I i
Com a aproximação dos halteres (
I i i  I f  f
If
<
Ii
) a velocidade angular do sistema aumenta
EXEMPLO 2: CONSERVAÇÃO DO MOMENTO ANGULAR
Queremos calcular a velocidade angular final do sistema após o homem
inverter o eixo de rotação da roda de bicicleta
Dados
Ibic  1, 2 kg.m2 ; Itot  6,8 kg.m2 e i  3,9 rot/s
Momento angular inicial do sistema
bicicleta-homem (+ banco)
roda de
Li  Lbic  I bici
Agora o homem inverte o eixo de rotação da
roda de bicicleta
Lbic   Li
EXEMPLO 2 (cont): CONSERVAÇÃO DO MOMENTO ANGULAR
Momento angular final do sistema:
L f  Lbic  Lmen  Lmen  Li
Há conservação do momento angular 
uma vez que só há forças internas no
sistema
L f  Li  Lmen  Li  Li
 Lmen  2 Li
I tot  2I bici
2 I bic i
 
 1,4
I tot
rot/s
Exemplo 3: CONSERVAÇÃO DO MOMENTO ANGULAR
No caso da mergulhadora da figura ao lado o CM segue um movimento parabólico

I   mi ri 
i

LL
onde



dL

 0  L  const.
dt

L
e o momento angular
da nadadora é constante
durante o salto. Juntando braços e pernas, ela pode
aumentar sua velocidade angular em torno do eixo
que passa pelo CM, às custas da redução do momento
de inércia em relação a este eixo

Mg
Mg
QUANDO O MOMENTO ANGULAR VARIA COM O TEMPO
dL d
d
 ( I )  I
 I
dt dt
dt
ou


M  I
que é semelhante à equação de Newton


F  ma
ROLAMENTO DE UM CORPO RÍGIDO
Consideramos que um cilindro gira de um ângulo
O centro de massa desloca-se de
s  r
PARA O MOVIMENTO DE ROLAMENTO PURO
Velocidade do centro de massa
vCM
ds
d

R
 R
dt
dt
Aceleração do centro de massa
aCM
dvCM
d

R
 R
dt
dt

.