Apresentação do PowerPoint - Prof. Alex Física e Matemática

1) Um astrônomo, ao estudar a estrela dupla E1 e E2, observou que
ambas executavam um movimento circular uniforme em torno do
ponto P, como se estivessem ligadas por uma barra imaginária. Ele
mediu o período dos movimentos das estrelas obtendo T = 12 dias.
a)
b)
c)
d)
X
E2
E2
E1
E2
E1
P
E1
P
r1
r2
P
E2
P
e)
P
P
E1
E1
E2
E2
P
E2
E1
Observou ainda que o raio r1 da trajetória de E1 era três vezes menor
do que o raio r2 da trajetória E2. Se, em uma dada observação, as
estrelas ocupavam as posições indicadas na figura e se movem no
sentido indicado pelas setas, assinale a alternativa na qual estão
corretamente indicadas as posições das estrelas 15 dias depois
E1
2) Em uma estrada, dois carros A e B entram simultaneamente em
curvas paralelas com raios rA e rB. O velocímetro de ambos os
carros indicam, ao longo de todo o trecho curvo, valores constante
vA e vB. Se os carros saem das curvas ao mesmo tempo, a relação entre VA e VB
é:
A
B
rB
rA
A = B
VA = A . rA VB = B . rB
A = VA
rA
B = VB
rB
A = B
a)
b)
X
c)
d)
e)
VA = vB
vA / vB = rA / rB
Va / vB = (rA / rB)²
vA / vB = rB / rA
vA / vB = (rB / rA)²
VA
VB
=
rA
rB
VA = rA
VB rB
3) Considere que a Lua descreve uma órbita circular
uniforme em torno da Terra. Assim sendo, assinale a
opção em que estão representadas a resultante (Fr)
sobre o satélite e a sua velocidade (v)
a)
b)
V
Fr
V
Fr
X
d)
c)
V
Fr = 0
e)
V
Fr
V
Fr
A Força Resultante tem a mesma direção e o mesmo sentido que
a aceleração centrípeta.
A aceleração centrípeta é perpendicular à velocidade e tem o
sentido para o centro da trajetória.
4) Os princípios básicos da mecânica foram estabelecidos por
Newton e publicados em 1686, sob o título “Princípios
Matemáticos da Filosofia Natural”. Com base nestes
princípios, é correto afirmar:
A) A aceleração de um corpo em queda livre depende da massa
desse corpo.
B) As forças de ação e reação são forças de mesma intensidade e
estão aplicadas em um mesmo corpo.
C) A massa de um corpo é uma propriedade desse corpo e do
local onde se encontra.
D)
X Quanto maior for a massa de um corpo, maior será a sua
inércia.
E) A lei da inércia, que é uma síntese das idéias de Galileu sobre
a inércia, afirma que, para manter um corpo em movimento
retilíneo uniforme, é necessária a ação de uma força
5) Um motorista é obrigado a frear um veículo de massa M que
se movimenta sobre uma estrada retilínea e horizontal com
velocidade 20 m/s (72 km/h). Admitindo-se que o processo de
retardamento se deva exclusivamente a ação do atrito, que tem
intensidade igual a 50% da componente normal da força de
contato, a distância necessária para o carro parar é, em metros:
(adote g = 10 m/s²)
N
pára
Vo=20m/s
V=0
A) 20
P=m.g
P=N
A
B) 30
P = m . 10
S = ?
C) 40
P = 10m
Fr = A
P
D) 50
V² = Vo² + 2 . a . S
N = 10m
A = 50% N
E) 60
0² = 20² + 2 .(- 5) . S
Fr = m . a A = 50/100 . 10m
A=5m
0 = 400 - 10 . S
5m = m . a
x
a = 5m
m
10 S = 400 S = 400 / 10
a = 5 m/s²
S = 40 m
6) Um corpo de massa 10 kg está em repouso
sobre um plano horizontal com o qual o atrito é
desprezível. Determinar a intensidade da força
horizontal (F) constante que se deve aplicar ao
corpo para que ele desloque 40 m em 4 s.
a)
xb)
c)
d)
e)
25 N
50 N
75 N
100 N
125 N
m = 10 kg
Vo = 0
F = FR
S = 40 m
t = 4 s
FR = m . a
S = Vo . t + a/2 . t²
FR = 10 . 5
40 = 0 . 4 + a/2 . 4²
40 = 0 + a/2 . 16
FR = 50 N
40 = 8.a
40 = a
8
a = 5 m/s²
7) Um corpo de massa 3 kg percorre uma trajetória retilínea
sobre uma superfície plana horizontal. O gráfico da velocidade
em função do tempo de seu movimento é o indicado na figura.
20
V (m/s)
t (s)
4
a)
b)
c)
d)
e)
X
4s
5s
9s
12 s
14 s
t = 10 s
m = 3 kg
Vo = 20 m/s
FR = 6 N
tp = ?
V = 0 (pára)
tp=14
Sabendo-se que uma força F
horizontal constante de
intensidade 6,0 N age sobre o
corpo apenas no intervalo 0 a
4 s e que, durante todo o
movimento a intensidade do
atrito é constante, o instante
(tp) em que o corpo pára vale:
V = Vo + a . t
FR = m . a
0 = 20 - 2 . t
6 = 3 . a 6 /3 = a 2 . t = 20 t = 20 / 2
a = 2 m/s²
t = 10 s
8) A figura 1 a seguir representa uma esfera de massa m, em
repouso, suspensa por um fio inextensível de massa desprezível. A
figura 2 representa o mesmo conjunto oscilando como um
pêndulo, no instante em que a esfera passa pelo ponto mais baixo
de sua trajetória.
A respeito da força de tração no
Figura 1
Figura 2
fio e do peso da esfera
respectivamente, no caso da
Figura 1 (T1 e P1) e no caso da
Figura 2 (T2 e P2), podemos
FR T2
T1
dizer que:
P1
P1 = T1
P1 = P2
P2
FR = T2 – P2
T2 > T1
a)
b)
c)
d)
e)
X
T1 = T2 e P1 = P2
T1 > T2 e P1 = P2
T1 = T2 e P1 < P2
T1 < T2 e P1 > P2
T1 < T2 e P1 = P2
9) Um pêndulo cônico é constituído por uma esfera de pequenas
dimensões presa por meio de um fio a um ponto fixo e que é
posta para girar em uma trajetória plana, circular e horizontal.
Observe que não existe superfície de apoio para a esfera da
figura.
Xa)
b)
T
c)
d)
P
Desprezando a resistência do
ar, assinalar a alternativa na
qual estão corretamente
assinaladas as forças que agem
na esfera
e)
10) Uma espaçonave desloca-se com velocidade constante de
10³ m/s. Acionando-se seu sistema de aceleração durante 10 s,
sua velocidade aumenta uniformemente para 104 m/s
mantendo-se em trajetória retilínea. O deslocamento escalar
da espaçonave nesse intervalo de tempo é:
X
a)
b)
c)
d)
e)
5,5 . 104 m
104 m
5,5 . 10³ m
3,5 . 10³ m
10³m
a = V
t
Dados:
Vo = 10³ m/s
V = 104 m/s
t = 10 s
S = ?
a = 104 – 10³
10
a = 10000 – 1000 a = 9000
10
10
a = 900 m/s² a = 9.10² m/s²
V² = Vo² + 2 . a . S
(104)² = (10³)² + 2 . (9.10²) . S
108 = 106 + 18.10² . S
100000000 - 1000000 = 18.10² . S
99000000 = 18.10² . S
99.106 = 18.10² . S
6
99.10
S =
18.10²
S = 5,5 . 104 m
11) Uma polia gira em torno de um eixo em movimento de
rotação uniforme.
Se a velocidade do ponto A, que está a
5 cm = 0,05 m
5 cm do eixo de rotação, é 3,14 m/s,
podemos afirmar que: (  = 3,14)
V=.r
 = 2  .f
3,14 =  . 0,05
62,8 = 6,28 .f
= 3,14 / 0,05
62,8 = 2. 3,14 .f
62,8 / 6,28 = f
Dados:
= 62,8 rad/s
r=0,05m

é igual em todos os pontos f = 10 Hz (x60) f=600 rpm
V=3,14m/s
a)
X A freqüência do movimento de rotação da polia é 600 rpm
b) A freqüência do movimento de rotação da polia é 600 HZ
c) A velocidade angular do movimento de rotação da polia é 600 rad/s
d) Todos os pontos da polia apresentam velocidade escalar = 3,14 m/s
e) A freqüência do movimento de rotação da polia é 10 rpm
12) Um corpo de pequenas dimensões está preso por meio de um fio
ideal a um ponto fixo. O corpo é colocado para se movimentar em
trajetória circular, horizontal.
Sabendo-se que a velocidade escalar do
movimento é constante e que a resistência
do ar é desprezível nas condições da
experiência, está correto afirmar que:
a) O corpo está submetido a ação de duas
forças e a resultante delas é nula.
b) O corpo está submetido a ação de três forças
T
e a resultante delas é nula.
c) O corpo está submetido a ação de três forças
e a resultante delas é diferente de zero.
P
d) O corpo está submetido a ação de uma única
força.
e)
X O corpo está submetido a ação de duas
forças e a resultante delas é diferente de
zero.
13) Na figura está indicado o gráfico da velocidade em função do
tempo de um corpo de massa 3 kg em trajetória retilínea.
V(m/s)
12
8
t (s)
Dados :
m = 3 kg
Vo = 8 m/s
V = 12 m/s
t = 2 s
2
A intensidade da resultante das
forças que agem sobre ele é :
a)
b)
c)
d)
X
e)
36 N
24 N
12 N
6N
2N
a = V
t
a = 12 - 8
2
a= 4
2
a = 2 m/s²
FR = m . a
FR = 3 . 2
FR = 6 N
14) Com relação a um corpo em repouso apoiado sobre uma mesa
plana horizontal, são feitas quatro afirmações:
I. Peso e Normal não constituem par ação e reação. certo
II. A reação do Peso está no centro da Terra. certo
III. Normal e Peso não apresentam necessariamente a mesma
intensidade. certo
IV. A força que o corpo aplica no apoio é o seu Peso. errado
A força que o corpo aplica no apoio é a Normal.
Assinale a alternativa correta:
a)
b)
c)
X
d)
e)
Nenhuma afirmação está correta
Apenas uma afirmação é correta
Há apenas duas afirmações corretas
Há apenas três afirmações corretas
Todas afirmações estão corretas.
15) Um corpo de massa 100g desliza sobre um plano horizontal
sem atrito em MCU preso por meio de um fio de comprimento 20
cm a um ponto fixo.
N
T
r = 0,20m
P
Dados:
m = 100 g (:1000) = 0,1 kg
r = 0,20 m
f = 600 rpm (:60) = 10 Hz
P=N
FR = T
 = 2  .f
 = 2  .10
 = 20  rad/s
Se a freqüência do movimento é
FR = m . ac
600 rpm, a intensidade da força de
tração no fio vale aproximadamente:
ac = ² . r
(² = 10)
ac = (20  )² . 0,2
T
=
m
.
ac
a) 800 N
b)
X 80 N
ac = 4000 ² . 0,2
T
=
0,1
.
800
c) 40 N
d) 20 N
ac = 800 m/s²
T
=
80
N
e) 10 N
16) Num local onde g = 10 N/kg um corpo de massa 20 kg apoia-se
sobre o piso de um elevador que desce em movimento retardado
com aceleração |a | = 3 m/s². A intensidade da força que o corpo
troca com o piso vale:
a)
b)
c)
d)
X
e)
20 N
140 N
200 N
260 N
600 N
elevador
desce retardado
a
FR
N>P
V
N
FR = m . | a |
N- P=m. |a|
P
A força que o corpo troca
com o apoio é a Normal
N - 200 = 20 . 3
P=m.g
P = 20 . 10
P = 200 N
N - 200 = 60
N = 60 + 200
N = 260 N
17) Um corpo se desloca em uma trajetória retilínea e horizontal.No
instante t = 0 seu movimento é para a direita. Sua velocidade pode
ser calculada em cada instante pela expressão V = 12 – 4 . t (SI).
Assinalar a alternativa na qual estão descritas as características da
velocidade vetorial desse corpo no instante 5 s.
a)
b)
c)
X
d)
e)
Intensidade 8 m/s; direção horizontal; sentido para a esquerda.
Intensidade 8 m/s; direção horizontal; sentido para a direita.
Intensidade – 8 m/s; direção horizontal; sentido para a esquerda.
Intensidade – 8 m/s; direção horizontal; sentido para a direita.
Intensidade 8 m/s; direção para a esquerda; sentido horizontal.
V = 12 – 4 . t
V = 12 – 4 . 5
V = 12 – 20
V = - 8 m/s
Em t = 0 a V = 12 m/s (Vo = 12 m/s) positiva e movimentando-se
para a direita. Portanto se a velocidade passa a ser negativa é porque
está se movimentando em sentido contrário: para a esquerda.
18) Motoristas que dirigem de modo prudente sabem da necessidade de
manter uma certa distância do veículo da frente para evitar colisões. Sabem
também que a distância adequada depende principalmente da velocidade do
veículo, do estado dos pneus, do tipo e do estado do pavimento.
Preocupado com esse problema, um motorista resolve realizar algumas
medidas em uma pista retilínea e horizontal. Descobre que precisa de 40 m
para parar o seu carro quando esse se movimenta a 72 km/h (20 m/s).
Supondo que a causa de retardamento do veículo seja exclusivamente ao
atrito, ele pode concluir que:
(g=10m/s²)
a) O resultado encontrado vale para qualquer pista.
b) Seriam necessários 20m para parar o mesmo veículo na mesma
pista, se ele se movimentasse a 36 km/h (10 m/s).
c)
X Nas mesmas condições do problema, a intensidade do atrito é a
metade da intensidade da Normal.
d) Nas condições do problema, o atrito tem a mesma intensidade da
Normal
e) A distância necessária para parar um veículo em uma determinada
pista é diretamente proporcional à sua velocidade.
Resolução do exercício 18
Dados:
A pista é retilínea e horizontal
S = 40 m
V² = Vo² + 2 . a . S
Vo = 20 m/s
g = 10 m/s²
0² = 20² + 2 . a . 40
FR = Atrito
P=m.g
P=N
P = m . 10
P = 10 m
N= 10m
0 = 400 + 80 a
80 a = - 400
a = - 400
80
a = 5 m/s²
FR = A
FR = m . | a |
A=m. |5|
A=5m
O Atrito tem a metade da intensidade da Normal
19)Uma resultante de 20 N age sobre um corpo de massa 4,0
kg durante 2,0 s. Se o corpo parte do repouso, seu
deslocamento no intervalo de tempo em que a força atuou é :
a)
X
b)
c)
d)
e)
20 m
10 m
5m
2,5 m
2,0 m
Dados:
FR = 20 N
m = 4 kg
t = 2 s
Vo = 0
S = ?
FR = m . | a |
20 = 4 . a
a = 20 / 4
a = 5 m/s²
S = Vo . t + a/2 . t²
S = 0 . 2 + 5/2 . 2²
S = 5/2 . 4
S = 10 m
20) Durante uma brincadeira, Bárbara arremessa uma bola de
vôlei verticalmente para cima, como mostrado na figura.
Assinale a alternativa cujo diagrama melhor representa a(s) força(s) que
atua(m) na bola no ponto mais alto de sua trajetória.
a)
b)
c)
X
d)
e)
Nenhuma força
atua sobre a bola
nesse ponto
21) Um fio de comprimento L prende um corpo de peso P e dimensões
desprezíveis ao teto. Deslocado lateralmente o corpo recebe um
impulso horizontal e passa a descrever um movimento circular
uniforme num plano horizontal, de acordo com a figura a seguir.
A resultante das forças que agem sobre o corpo tem intensidade:


T
P
T
FR
a) T
b) P
d) Pcos 
P
sen  = FR
T
c) T - P
FR = Tsen 
e) Ptg 
X
cos  = P
T
tg  = FR
P
FR = Ptg 
22) É comum as embalagens de mercadorias apresentarem a expressão
“Peso líquido”. O termo líquido sugere que o valor indicado na
embalagem corresponde apenas ao conteúdo. Em umpote de mel podese ter a frase: “peso líquido 500g”. Nesse sentido, analise quantoà
coerência com os sistemas de unidades adotados na Física, se as
afirmativas a seguir são falsas ou verdadeiras, na medida em que a
frase indicada na embalagem.
F I) A inscrição está certa, pois o peso é uma força e,portanto pode ser
expresso em gramas.
VII) A inscrição estaria certa se fosse “massa líquida 500 g”.
F III) A inscrição está certa porque g é o campo gravitacional e P = m.g
VIV) A inscrição está errada,porque o peso não pode ser expresso em
gramas.
a) I e II verdadeiras, III e IV falsas
A combinação correta é:
b) I e III falsas, II e IV verdadeiras
X
c) I e IV falsas, II e III verdadeiras
d) I e II e III falsas, IV verdadeira
e) I e III e IV verdadeiras, II falsa
23) Uma partícula de massa igual a 10 kg é submetida a ação de
duas forças perpendiculares entre si de 3N e 4N. Pode se afirmar
que o módulo de sua aceleração é:
a)
b)
X
c)
d)
e)
5,0 m/s²
50 m/s²
0,5 m/s²
7,0 m/s²
0,7 m/s²
FR
FR² = F1² + F2²
FR² = 3² + 4²
FR² = 9 + 16
FR² = 25
FR = m .  a 
5 = 10 .  a 
a = 5 / 10
a = 0,5 m/s²
FR = 5 N
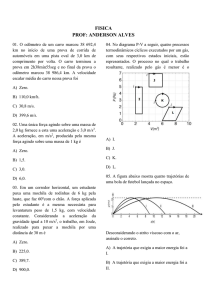
24) O elevador de passageiros começou a ser utilizado em meados do
sec XIX, favorecendo o redesenho arquitetônico das grandes cidades e
modificando os hábitos de moradia.
Suponha que o elevador de um prédio sobe com aceleração constante
de 2 m/s², transportando passageiros cuja massa total é de 5,0x10² kg.
Durante esse movimento de subida, o piso do elevador fica submetido
à força de:
dado: aceleração da gravidade = 10 m/s²
a)
b)
c)
d)
e)
X
5,0x10² N
1,5x10³ N
4,0x10³ N
5,0x10³ N
6,0x10³ N
Elevador sobe acelerado
N
N>P
a
FR
V
FR = m.a 
N–P =m.a
P
P=m.g
P = 500 . 10
P = 5000 N
N – 5000 = 500 . 2
N – 5000 = 1000
N = 5000 + 1000
N = 6000 N
25) Considere um ventilador com hélice girando. Em relação aos
pontos da hélice, é correto afirmar que:
Xa) Os pontos mais afastados do eixo de rotação tem maior
velocidade linear (escalar).
b) Todos têm a mesma aceleração centrípeta.
c) Os pontos mais afastados do eixo de rotação têm maior
velocidade angular.
d) Os pontos mais afastados do eixo de rotação têm menor
aceleração centrípeta.
e) Todos têm a mesma velocidade linear (escalar).
V = . r
Quanto maior o raio maior a velocidade V
26) Um “motoboy” muito apressado,deslocando-se a 30 m/s, freou
para não colidir com um automóvel a sua frente. Durante a
frenagem, sua moto percorreu 30 m de distância em linha reta,
tendo sua velocidade uniformemente reduzida até parar, sem bater
no automóvel.
O módulo da aceleração média da moto, em m/s², enquanto
percorrida a distância de 30 m, foi de :
a)
b)
X
c)
d)
e)
10
15
30
45
108
Dados:
Vo = 30 m/s
V=0
S = 30 m
V² = Vo² + 2 . a . S
0² = 30² + 2 . a . 30
0 = 900 + 60 a
60 a = - 900
a = - 900 / 60
a = - 15 m/s²
a = 15 m/s²
em módulo
27) A velocidade de um móvel aumenta, de maneira uniforme, 2,4
m/s a cada 3,0 s. Em certo instante, a velocidade do móvelé de 12
m/s. A partir desse instante, nos próximos 5,0 s a distância
percorrida pelo móvel, em metros é:
a)
b)
c)
d)
X
e)
10
30
60
70
90
Dados:
v = 2,4 m/s Vo = 12 m/s
t =3 s
t=5s
S = ?
V² = Vo² + 2 . a . S
a = V
t
a = 2,4
3
a = 0,8 m/s²
V = Vo + a . t
V = 12 + 0,8 . 5
16² = 12² + 2 . 0,8 . S
256 = 144 + 1,6 . S
1,6 . S = 256 - 144
V = 12 + 4
1,6 . S = 142
V = 16 m/s
S = 142/ 1,6
S = 70 m
28) Um carro está viajando numa estrada retilínea com a
velocidade de 72 km/h. vendo adiante um congestionamento no
trânsito, o motorista aplica os freios durante 2,5s e reduz a
velocidade para 54 km/h. Supondo que a aceleração é constante
durante o período de aplicação dos freios, calcule o seu módulo,
em m/s².
Dados:
a) 2,0
X
Vo = 72 km/h (:3,6 ) = 20 m/s
b) 2,5
V = 54 km/h (:3,6) = 15 m/s
c) 5,0
t = 2,5 s
d) 7,2
a =?
e) 18
V = Vo + a . t
5 = a . 2,5
20 = 15 + a . 2,5
a = 5 / 2,5
20 - 15 = a . 2,5
a = 2 m/s²