ch22 pw

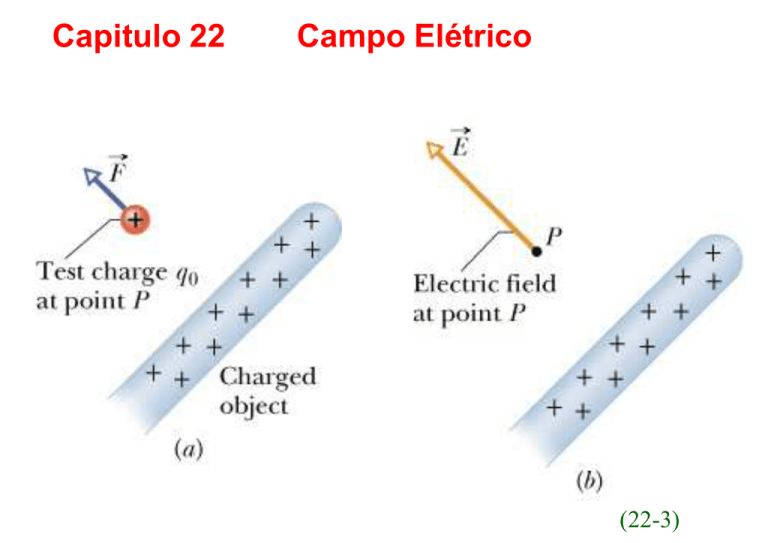
Capitulo 22
Campo Elétrico
(22-3)
Campo Elétrico Produzido por uma carga Pontual
r
E
qo P
q
(22-4)
r
q
E=
4πε o r 2
1
Exemplo 22.1
(22-5)
Exercício 22.5 O núcleo de um átomo de plutônio 239
contém 94 prótons. Suponha que o núcleo é uma esfera
com 6,64 fm (fento 10-15) de raio e que a carga dos
prótons está distribuída uniformemente na esfera.
Determine (a) o módulo e (b) o sentido (para dentro ou
para fora) do campo elétrico produzido pelos prótons
na superfície do núcleo.
Campo Elétrico Produzido
por um Dipolo Elétrico
Exemplo 22.2
Campo Elétrico Produzido Por Várias Cargas
dE
P
r
r̂
dV
dq
(22-8)
Campo Elétrico Produzido
Por Uma Linha de Cargas
A
(22-9)
dq
C
Exemplo 22-3
Campo Elétrico Produzido
Por Um Disco Carregado
Experimento da Gota de Millikan
+++++++
--------
A força eletrostática F que age sobre uma partícula carregada
submetida a um campo elétrico E tem o mesmo sentido que E se a
carga q da partícula for positiva e o sentido oposto se a carga q for
negativa.
Impressoras Jato de Tinta
Um dipolo em um campo elétrico
Um dipolo em um campo elétrico
F+
Fx-axis
r
Fnet = 0
r r
τ = p× E
r
(22-14)
Exemplo 22.5
•Exercício 22.15 A Fig. 22-35 mostra um prótons (p) no eixo
central de um disco com uma densidade uniforme de cargas devido
a um excesso de elétrons. Três dos elétrons são mostrados na
figura: o elétron ec, no centro do disco, e os elétrons es, em
extremidades opostas do disco, a uma distância R do centro. O
próton se encontra inicialmente a uma distância z = R = 2,00 cm do
disco. Com o próton nessa posição, determine o módulo (a) do
campo elétrico Ec produzido pelo elétron ec e (b) do campo elétrico
total Es,tot produzido pelos elétrons es. O próton é transferido para o
ponto z = R/10,0. Determine os novos valores (c) do módulo de Ec
e (d) do módulo de Es,Tot. (e) Os resultados dos itens (a) e (c)
mostram que o módulo de Ec aumenta quando o próton se aproxima
do disco. Por que, nas mesmas condições, o módulo de Es,Tot
diminui, como mostram os itens (b) e (d)?
Exercício 22.60 Um dipolo elétrico e ́submetido a um
campo elétrico uniforme E cujo módulo é 20 N/C.
A Fig. 22-57 mostra a energia potencial U do dipolo em
função do ângulo u entre E e o momento do dipolo p. A
escala do eixo vertical é definida por Us = 100 . 10-28 J.
Qual é o módulo de p?
Lista Exercícios Cap. 22
5, 7, 13, 15, 17, 19, 23, 25, 29, 31, 35, 37, 43,
49, 53, 59
Exercício 21-9 (8ª Ed.) Na Fig. 21-24, as cargas das partículas são
q1 = -q2 = 100nC e q3 = -q4 = 200 nC. O lado do quadrado é
a = 5,0 cm. Determine (a) a componente x e (b) a componente y da
força eletrostática a que está submetida a partícula 3.
Exercício 21-31 (8ª Ed.) Calcule o número de coulombs de carga
positiva que estão presentes em 250 cm3 de água (neutra).
(Sugestão: um átomo de hidrogênio contém um próton; um átomo
de oxigênio contém oito prótons.)
Potential energy of an electric dipole
in a uniform electric field
θ
θ
90°
90°
U = − ∫ τ dθ ′ = − ∫ pE sin θ dθ ′
θ
r r
U = − pE ∫ sin θ dθ ′ = − pE cos θ = − p ⋅ E
U = − pE cos θ
r r
U = −p⋅E
90°
r
r E
p
At point A (θ = 0) U has a minimum
B
value U min = − pE
U
θ
180˚
A
(22-15)
It is a position of stable equilibrium
At point B (θ = 180°) U has a maximum
value U max = + pE
It is a position of unstable equilibrium
r
p
r
E
r
p
θi
Fig.a
r
E
r
p
Work done by an external agent to rotate an electric
dipole in a uniform electric field
Consider the electric dipole in Fig.a. It has an electric
r
r
dipole moment p and is positioned so that p is at an angle
r
θi with respect to a uniform electric field E
An external agent rotates the electric dipole and brings
θf
Fig.b
r
E
it in its final position shown in Fig.b. In this position
r
r
p is at an angleθ f with respect to E
The work W done by the external agent on the dipole
is equal to the difference between the initial and
final potential energy of the dipole
W = U f − U i = − pE cos θ f − ( − pE cos θi )
W = pE ( cos θi − cos θ f
(22-16)
)