Pré-Reguladores de Fator de Potência – Cap. 5
J. A. Pomilio
5. CONVERSOR ABAIXADOR DE TENSÃO COMO PFP
O conversor abaixador de tensão (buck ou forward, se for isolado) tem uso muito restrito
como PFP, uma vez que introduz uma zona de corrente nula na entrada. Isto ocorre quando a
tensão de entrada é menor do que a tensão de saída. Alternativamente, é possível alto FP desde
que se opere com um controle MLP dentro de cada semiciclo da rede.
5.1
Conversor abaixador de tensão com entrada CC
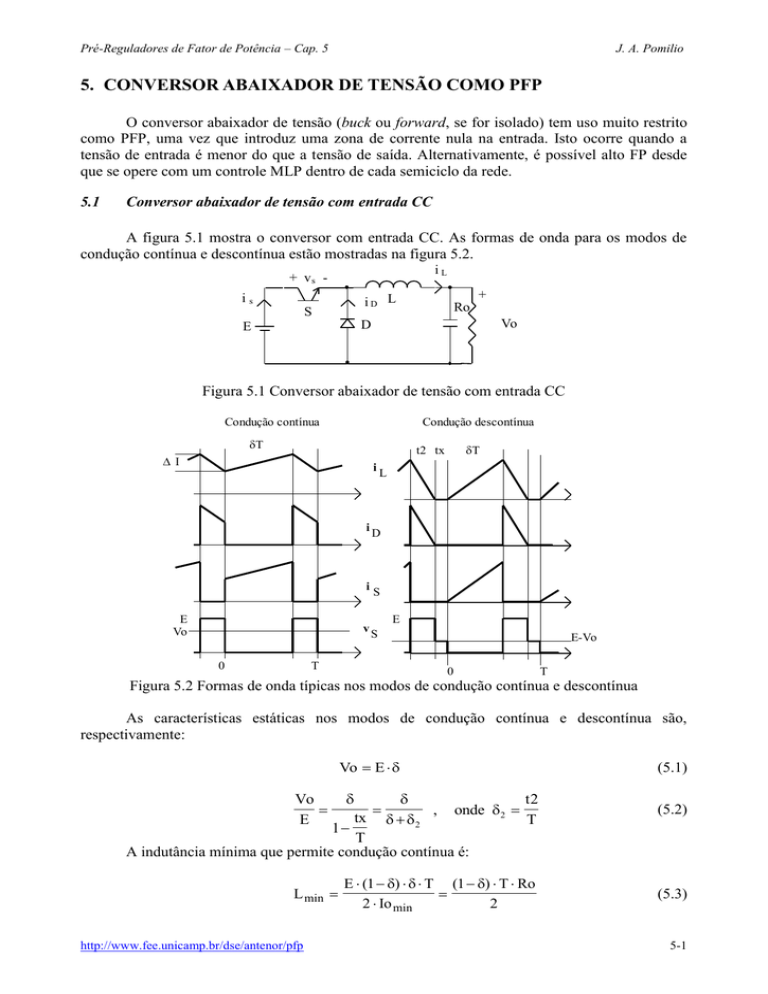
A figura 5.1 mostra o conversor com entrada CC. As formas de onda para os modos de
condução contínua e descontínua estão mostradas na figura 5.2.
iL
+ vs is
+
iD L
S
Ro
Vo
D
E
Figura 5.1 Conversor abaixador de tensão com entrada CC
Condução contínua
Condução descontínua
T
T
t2 tx
I
i
L
iD
i
E
Vo
v
0
S
E
S
E-Vo
T
0
T
Figura 5.2 Formas de onda típicas nos modos de condução contínua e descontínua
As características estáticas nos modos de condução contínua e descontínua são,
respectivamente:
Vo E
Vo
E
,
2
(5.1)
t2
T
(5.2)
E (1 ) T (1 ) T Ro
2 Io min
2
(5.3)
onde 2
tx
1
T
A indutância mínima que permite condução contínua é:
L min
http://www.fee.unicamp.br/dse/antenor/pfp
5-1
Pré-Reguladores de Fator de Potência – Cap. 5
5.2
J. A. Pomilio
Conversor abaixador de tensão como PFP
O conversor abaixador de tensão operando como PFP está mostrado na figura 5.3. A
posição do transistor permite a proteção contra sobrecorrentes e partida suave.
A figura 5.4. mostra as formas de onda típicas para condução descontínua no indutor,
indicando também a corrente pela rede (após filtragem) e seu espectro.
Vac
+
L
ii
S
Ro
D
Vo
Figura 5.3. Conversor abaixador de tensão como PFP
Vi
MO
NIC
FR
EQ
UE
NC
Y
FO
Vo
HA
RM
ONI
C
FR
EQ
UE
Figura 5.4. Formas de onda típicas de conversor abaixador de tensão como PFP e espectro da
corrente filtrada (THD=53%)
O ângulo até o qual não há corrente na entrada é dado por:
Vo
a sin
Vp
Onde: Vp é o valor de pico da tensão de alimentação e t.
A evolução da corrente média de entrada é:
i i I p sin(t ) sin()
(5.4)
válido para >t>
(5.5)
O valor de pico desta corrente é calculado no pico da tensão da rede e é obtido através da
área relativa à corrente instantânea de entrada:
Ip
Vp 2 T
(5.6)
2L
A potência média (ativa) de entrada, calculada em meio ciclo da rede é [5.1]:
1
Pi
Vp I p sin() sin() sin() d
http://www.fee.unicamp.br/dse/antenor/pfp
Vp I p 2 sin(2)
2
(5.7)
5-2
Pré-Reguladores de Fator de Potência – Cap. 5
J. A. Pomilio
A corrente eficaz de entrada é:
I iRMS
Vp T
3 L
X()
(5.8)
3 sin(2 )
X() 2 cos(2 )
2
2
(5.9)
Considerando o efeito do chaveamento de alta frequência, pode-se fazer o cálculo do fator
de potência. O valor obtido é:
2 sin(2) 6
(5.10)
FP
4 X()
Para , a equação (5.10) fornece um resultado igual ao do conversor abaixadorelevador de tensão visto anteriormente (0,866).
A figura 5.5 mostra o valor do FP em função da tensão de saída (M=Vo/Vp=1/). Observe
que quanto maior a tensão de saída, pior o fator de potência, uma vez que a corrente se concentra
próxima ao pico da tensão. Dada a dependência da largura de pulso, para valores reduzidos de ,
o FP se reduz sensivelmente, pois ocorre um aumento no conteúdo harmônico da corrente. Uma
melhoria no FP é obtida com a inclusão de um capacitor de filtro, junto ao retificador, o qual
oferece um caminho de baixa impedância para as componentes harmônicas, de modo que,
idealmente, pela linha circula apenas o valor médio da corrente pulsada de entrada.
Se forem considerados os limites da norma IEC, é possível, dentro de certas faixas de
operação, utilizar este conversor [5.2].
FP
0.9
0.8
0.7
0.6
0.5
0
0.1
0.2
0.3
0.4
0.5
0.6
Figura 5.5. Variação do fator de potência com a tensão de saída, para diferentes valores de ciclo
de trabalho, considerando o efeito do chaveamento em alta frequência.
O fator de potência obtido através do valor médio da corrente será:
FP
2 sin( 2 )
1
3 sin( 2 ) ( 2 ) cos( 2 )
2
2
2
2
(5.11)
Observa-se na figura 5.6 que quando a tensão de saída tende a zero o fator de potência
tende à unidade (considerando a corrente média de entrada, ou seja, desprezando as componentes
de alta frequência na análise). À medida que aumenta a tensão de saída, como o ângulo
aumenta, o FP diminui.
http://www.fee.unicamp.br/dse/antenor/pfp
5-3
Pré-Reguladores de Fator de Potência – Cap. 5
1
J. A. Pomilio
FP
0.8
0.6
0.4
0.2
0
0
0.2
0.4
0.6
0.8
1
M
Figura 5.6 Fator de potência de conversor abaixador de tensão como PFP (considerando a
corrente média de entrada).
Outra possibilidade é utilizar uma indutância de saída elevada o suficiente de modo que,
pelo ajuste da largura de pulso do interruptor, seja possível sintetizar uma corrente senoidal
(depois de filtrada) na rede, como mostra a figura 5.7 [5.3], tendo as formas de onda indicadas na
figura 5.8. Como a corrente de saída é suposta constante, basta ter uma referência senoidal
(retificada) para produzir o sinal PWM que a corrente na entrada seguirá a forma desejada.
Figura 5.7 Conversor buck PFP, com elevada indutância de saída e controle MLP.
Seja M o índice de modulação, dado pela relação entre o valor de pico da corrente de
entrada, Ip e a corrente de saída, Io (suposta constante). M=Ip/Io. No caso limite (M=1) a
corrente de pico na entrada se iguala à corrente de saída para um ângulo de 90°. A largura de
pulso segue um comportamento senoidal, proporcional à tensão CA: M.sen
A tensão média de saída será igual ao valor médio da tensão sobre o diodo Do, já que a
tensão média sobre Lo é nula em regime permanente. Como sempre há corrente na entrada, a
tensão na saída do retificador é a tensão CA, em módulo, desprezando a queda em Li (o qual é
dimensionado para filtrar a frequência de chaveamento, tendo efeito mínimo em 60 Hz). Esta
tensão será “recortada” pelo transistor, de acordo com a largura de pulso Seja vd a tensão
instantânea sobre o diodo Do:
,
(5.12)
cujo valor médio resulta:
(5.13)
http://www.fee.unicamp.br/dse/antenor/pfp
5-4
Pré-Reguladores de Fator de Potência – Cap. 5
J. A. Pomilio
A filtragem da alta frequência é providenciada pelo par Lin-Cin. O fator de potência
resultante é unitário.
Compare-se o resultado (5.13) com o que ocorre com um retificador monofásico a diodos
com filtro L na saída, de forma de Io seja constante. Neste caso a corrente de entrada é quadrada,
com amplitude Io e amplitude da fundamental vale (4.Io/ver capítulo. A tensão média de
saída apresenta um valor maior:
(5.14)
Conclui-se que o processo de modulação reduz a corrente na entrada para dar a esta uma
forma senoidal e, com isso, reduz a tensão média máxima na saída.
Ao reduzir a indutância Lo, não é mais válida a suposição de Io constante. A ondulação
na corrente de saída produz uma distorção na corrente de entrada, visível na figura 5.8.b.
4.0
2.0
0
-2.0
-4.0
0s
I(L2)
I(L3)
5ms
V(Vin:+,Vin:-)/100
10ms
15ms
20ms
25ms
30ms
35ms
40ms
Time
a) Elevada indutância de saída e corrente senoidal na entrada.
4.0
2.0
0
-2.0
-4.0
0s
I(L2)
I(L3)
5ms
V(Vin:+,Vin:-)/100
10ms
15ms
20ms
25ms
30ms
35ms
40ms
Time
b) Redução na indutância de saída e distorção na corrente.
Figura 5.8 Formas de onda do conversor buck PFP com elevada indutância de saída (tensão de
entrada, corrente de entrada e corrente no indutor de saída).
A correção na forma da corrente exige que seja introduzida uma realimentação da corrente
de saída, como mostra a figura 5.9. A restrição que permanece é que o valor mínimo da corrente
em Lo seja sempre superior ao valor instantâneo (absoluto) da corrente da rede. Caso esta
restrição não seja atendida, haverá distorção da corrente, como mostra a figura 5.10.
http://www.fee.unicamp.br/dse/antenor/pfp
5-5
Pré-Reguladores de Fator de Potência – Cap. 5
J. A. Pomilio
Figura 5.9 Conversor buck PFP, com controle MLP e realimentação da corrente de saída.
4.0
2.0
0
-2.0
a)
-4.0
20ms
I(L2)
I(L3)
25ms
V(Vin:+,Vin:-)/100
30ms
35ms
40ms
45ms
50ms
55ms
60ms
Time
4.0
2.0
0
-2.0
-4.0
20ms
I(L2)
I(L3)
25ms
V(Vin:+,Vin:-)/100
30ms
35ms
40ms
45ms
50ms
55ms
60ms
b)
Figura 5.10 Formas de onda de conversor buck PFP com realimentação da corrente de saída. a)
corrente CC sempre maior que corrente CA. b) corrente CC inferior à corrente CA em algum
intervalo.
Time
O ângulo de máxima modulação ocorre quando as correntes se tangenciam. Considerando
forma de onda senoidal da corrente filtrada, segue-se tendo FP=1. A forma da corrente de saída
pode ser aproximada, considerando uma variação pico-a-pico Io:
(5.15)
A largura de pulso será máxima (=1) no ângulo em que as correntes de entrada e de saída
se tangenciam, implicando na máxima ondulação admissível na corrente de saída (sem distorcer a
corrente) e, assim, na mínima indutância Lo. A largura de pulso é dada por:
http://www.fee.unicamp.br/dse/antenor/pfp
5-6
Pré-Reguladores de Fator de Potência – Cap. 5
J. A. Pomilio
=
(5.16)
onde Ior=Io/Io.
Supondo Vo constante, a um aumento de carga (aumento de Io) corresponde um aumento
na corrente de entrada e, portanto, de Ip, na mesma proporção, não ocorrendo mudança no valor
do índice M. Como não mais segue um comportamento senoidal, o resultado de (5.13) será
diferente.
O ângulo no qual é máximo é aquele no qual a corrente de entrada mais se aproxima do
valor da corrente instantânea de saída. Quando as correntes se tangenciam, =1. De (5.16) tem-se:
(5.17)
Derivando (5.17) em relação a e igualando a zero, obtém-se o ângulo de largura de
pulso unitária e que determina o máximo ripple na corrente de saída para funcionamento sem
distorção na corrente. Tal ângulo é mostrado na figura 5.11.a, estando na faixa entre 45° e 90°.
Usando este resultado é possível conhecer a ondulação relativa da corrente de saída que garante a
operação correta do PFP e mantém operação em condução contínua, como mostra a figura 5.11.b.
Com esta última vinculação, usando (5.16) em (5.12), pode-se numericamente, determinar a
tensão média de saída em função de M, mostrada na figura 5.12. O valor de saída é normalizado
pela tensão de pico na entrada. Para M=1, o ripple de corrente deve ser nulo e o resultado
converge para o caso de Io constante.
(5.18)
a)
b)
Figura 5.11 a) Ângulo em que se obtém ; b) Variação relativa da corrente de saída Ior.
a)
b)
Figura 5.12 a) Largura de pulso no caso limite de ripple na corrente; b) Tensão média de saída
(normalizada pela tensão CA de pico) para Io constante (azul) e com ripple máximo na corrente
de saída (vermelho).
http://www.fee.unicamp.br/dse/antenor/pfp
5-7
Pré-Reguladores de Fator de Potência – Cap. 5
J. A. Pomilio
A figura 5.13 mostra a resposta do circuito a uma variação de carga. O regulador é um PI
que restabelece a tensão em seu valor (95 V) após três ou quatro ciclos da ocorrência da
perturbação (aumento de 50% na demanda de potência).
1
4.0
2
100V
0
-4.0
>>
50V
40ms
1
I(L2)
60ms
V(Vin:+,Vin:-)/100
80ms
2
100ms
120ms
140ms
160ms
180ms
190ms
V(L3:2)
Time
Figura 5.13 Regulação da tensão de saída: tensão CC com variação de carga (vermelha), tensão
CA (dividida por 100 - azul) e corrente na fonte (verde)
5.3
Referências Bibliográficas
[5.1]
J. Sebastián, J. A. Cobos, P. Gil and J. Uceda: “The Determination of the Boundaries
between Continuous and Discontinuous Conduction Modes in PWM DC-to-DC
Converters Used as Power Factor Preregulators”. Proc. of PESC ‘92, pp. 1061-1070.
Toledo, Spain, Jun. 1992.
G. Spiazzi: “Analysis of Buck Converters Used as Power Factor Preregulators”. Proc. Of
IEEE PESC’97, pp. 564-570, St. Louis, USA, June 1997.
I. Barbi and F. A. P. de Souza: “A Unity Power Factor Buck Pre-Regulator with
Feedforward of the Output Inductor Current”. Proc. of IEEE APEC 1999.
[5.2]
[5.3]
5.4
Exercício
1. Simule o circuito abaixo, adequando as condições iniciais de corrente nos indutores e
tensão nos capacitores para minimizar a duração do transitório inicial. Analise o
comportamento da corrente de entrada (distorção) em função de diferentes elementos de
filtragem na entrada. V3 é a portadora da MLP.
http://www.fee.unicamp.br/dse/antenor/pfp
5-8












