ε ε 5 3R = 2 3 1 R 1 1 =RR + ε ε

UFJF – MÓDULO III DO PISM – TRIÊNIO 2010-2012 – GABARITO DA PROVA DE FÍSICA
PARA O DESENVOLVIMENTO E A RESPOSTA DAS QUESTÕES, SÓ SERÁ ADMITIDO USAR CANETA ESFEROGRÁFICA AZUL OU PRETA
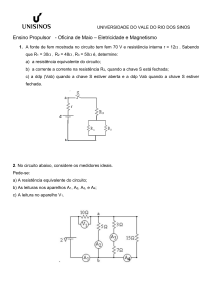
Questão 1 – Um estudante de física, com o intuito
de testar algumas teorias sobre circuitos e indução
eletromagnética, montou o circuito elétrico indicado
na figura ao lado. O circuito é composto de quatro
resistores com resistências elétricas R = 5kΩ
idênticas, uma chave S, uma fonte de fem ε = 150V
e um fio muito longo. Próximo a esse fio se encontra
uma bobina B no plano da página, ligada a um
amperímetro A, capaz de medir a corrente induzida
na bobina. Com base nessas informações, faça o
que se pede:
a) Calcule a corrente no circuito antes da chave S ser fechada.
Antes da chave S ser fechada temos duas resistências R em paralelo com uma resistência R conectada a uma
fonte de tensão ε. A resistência equivalente
como
ε = R eq I
R eq = R +
1
1 1
+
R R
=R+
R 3R
=
= 7,5Ω
2
2
temos que a corrente antes da chave ser fechada igual a
I=
2ε
= 20mA
3R
b) Calcule a corrente no circuito após a chave S ser fechada.
Após a chave S ser fechada temos uma resistências R em paralelo com a resistência equivalente do problema
anterior conectada a uma fonte de tensão ε. A nova resistência equivalente será,
R eq =
I=
1
1
1
+
R 3R
2
=
3R
, como ε = R eq I temos que a corrente após a chave ser fechada igual a
5
5ε
= 50mA . É possível também calcular as correntes nos dois ramos
3R
I=i1+i2=30mA+20mA=50mA
c) A corrente induzida na bobina imediatamente após a chave S ser fechada terá o mesmo sentido da
corrente no circuito? Justifique sua resposta.
Sim a corrente terá o mesmo sentido da corrente do circuito.
Justificativa: Como a corrente aumentou no circuito o campo magnético gerado pelo circuito na bobina
também cresceu e desta forma o fluxo também aumentou. Pela lei de Lenz, deve aparecer uma corrente
induzida tal que se oponha à variação de fluxo. Logo, se considerarmos a corrente convencional, no sentido
horário, no circuito deve aparecer uma corrente no mesmo sentido na bobina para se opor à variação de fluxo
criada pelo circuito.
1
UFJF – MÓDULO III DO PISM – TRIÊNIO 2010-2012 – GABARITO DA PROVA DE FÍSICA
PARA O DESENVOLVIMENTO E A RESPOSTA DAS QUESTÕES, SÓ SERÁ ADMITIDO USAR CANETA ESFEROGRÁFICA AZUL OU PRETA
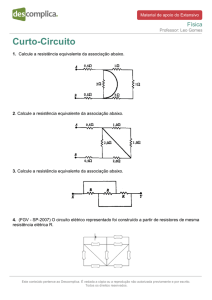
Questão 2 – Em uma região do espaço existe um campo elétrico
constante na direção x positiva, com intensidade de módulo
E0 = 8,0V/cm. Nessa região do espaço, é colocada uma partícula
com carga q1 = 10,0µC e massa m1 = 4,0µg. Essa partícula se
encontra na posição x1 = y1 = 0, como mostra a figura ao lado. Com
base nas informações acima, calcule os itens abaixo.
a) Calcule a força elétrica e a aceleração na carga.
A
força
elétrica
é
dado
F = q1 E = (q1E 0 ,0) ,
por:
V
-3
assim, Fx = 8,0 × 10 N = 8,0mN
m
Newton
temos
que FR = m a = (q 1 E 0 ,0)
então
Fy = 0,0 N
e
a y = 0 m/s 2
e
Fx = q 1 E 0 = 10,0 × 10 -6 C × 8,0 × 10 2
Da
segunda
ax =
lei
de
logo,
q1E 0
8,0 ×10-3 N
6
2
=
assim, a x = 2,0 × 10 m/s
-6
-3
m
4,0 ×10 ×10 kg
b) Calcule a diferença de potencial criada pelo campo elétrico E0 entre a origem e xb = 12,0cm.
A diferença de potencial será dado por,
Vab = E 0 ( x b − xa ) = 8,0
V
× (12,0 - 0,0)cm = 96,0 Volts .
cm
c) Considerando que a carga q1 é inserida com velocidade nula na origem, calcule a velocidade da carga na
posição xb = 12,0cm.
A variação da energia cinética da carga será igual ao trabalho realizado pelo campo elétrico que por sua vez
será igual ao produto da carga q 1 pela diferença de potencial entre a origem e o ponto x b . Logo,
m 2
(v f − vi2 ) = q 1 Vab como a velocidade inicial vi = 0,0m / s ,
2
obtemos,
vf =
2q 1 Vab
=
m
2 × 10,0 × 10 -6 × 96,0V
2
, assim, vf = 48,0 × 10 m / s ≅ 692,8m / s
4,0 × 10 -9 kg
2
UFJF – MÓDULO III DO PISM – TRIÊNIO 2010-2012 – GABARITO DA PROVA DE FÍSICA
PARA O DESENVOLVIMENTO E A RESPOSTA DAS QUESTÕES, SÓ SERÁ ADMITIDO USAR CANETA ESFEROGRÁFICA AZUL OU PRETA
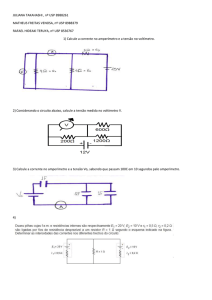
Questão 3 – Em 1913, o físico Dinamarquês Niels
Bohr (1885 - 1962) sugeriu uma explicação para o
espectro de energias do átomo de hidrogênio. Nesse
modelo, os elétrons carregados negativamente
circulavam com órbitas constantes em torno do núcleo
com carga positiva, de acordo com a Lei de Coulomb.
Os níveis de energia das órbitas constantes são dados
En =
por
−13,6eV
, em que n = 1, 2,3,... são os
n2
números quânticos que enumeram as possíveis
órbitas, assim como mostra a figura ao lado. Bohr
postulou que um elétron somente poderia passar de
uma órbita para outra mediante a absorção ou emissão
de um fóton. Com base nessas informações, sabendo
−15
que a constante de Planck é h = 4,1×10 eV.s e que a
8
velocidade da luz é c = 3,0×10 m/ s, calcule os itens
abaixo.
a) Considerando que o elétron estava inicialmente na órbita com n=1, calcule a frequência do fóton
necessária para excitar o elétron para o nível n = 4.
Da equação de Einstein temos,
E f = hf = E 4 − E1
assim a frequência do fóton será,
f =
E 4 − E1 − 0,85eV − (−13,6eV ) 12,75
=
=
× 1015 Hz = 3,1 × 1015 Hz
−15
h
4,1
4,1 × 10 eV ⋅ s
b) Suponha que o elétron, no estado excitado n = 4, possa decair para a órbita n = 2 e depois para a órbita
n = 1. Calcule quais seriam os comprimentos de onda λ dos fótons emitidos.
Da equação de Einstein e da relação c
= λf , temos, E f = hf 42 =
hc
λ 42
= E 4 − E1
logo o comprimento de onda será,
λ42
hc
4,1 × 10 −15 eV ⋅ s × 3,0 × 10 8 m / s 1,23 × 10 −6 m
=
=
=
≅ 482,3 × 10 −9 m = 482,3nm
E4 − E2
− 0,85eV − (−3,4eV )
2,55
Analogamente temos,
λ21 =
hc
4,1 × 10 −15 eV ⋅ s × 3,0 × 10 8 m / s 1,23 × 10 −6 m
=
=
≅ 120,5 × 10 −9 m = 120,5nm
E 2 − E1
− 3,4eV − (−13,6eV )
10,2
3
UFJF – MÓDULO III DO PISM – TRIÊNIO 2010-2012 – GABARITO DA PROVA DE FÍSICA
PARA O DESENVOLVIMENTO E A RESPOSTA DAS QUESTÕES, SÓ SERÁ ADMITIDO USAR CANETA ESFEROGRÁFICA AZUL OU PRETA
Questão 4 – Existem dois tipos de ondas sísmicas que se propagam através do interior da Terra: as ondas
primárias (ondas P) e as ondas secundárias (ondas S). As ondas P são longitudinais, enquanto as ondas S são
transversais e de menor velocidade que as ondas P.
Em uma estação sismológica (laboratório onde são estudados os terremotos), foi registrado o sinal de um abalo
provocado por um terremoto. O abalo ocorreu em um instante t0 e as ondas P e S, emitidas pelo abalo, foram
detectadas pela estação sismológica nos instantes de tempo tP e tS, respectivamente. As frequências da onda P e
da onda S são fP e fS e seus comprimentos de ondas são λP e λS, respectivamente. Com base nessas
informações, faça o que se pede:
a) Encontre uma expressão para o instante de tempo t0 em que as duas ondas foram emitidas pelo epicentro
do terremoto, em termos de fP, fS, λP, λS, tS e tp.
Igualando a distância d (entre o sismógrafo e o epicentro) percorrida pelas ondas S e P, obtemos:
d = vs (t s − t0 ) = v p (t p − t0 )
Onde vs e vp são as velocidades das ondas S e P respectivamente. Isolando t0 nesta última equação obtemos:
t0 =
Usando a relação v=λf para cada onda obtemos:
t0 =
v p t p −v s t s
v p − vs
λ p f p t p − λs f s t s
λ p f p − λs f s
b) Encontre uma expressão para a distância d do sismógrafo até o epicentro do terremoto em termos de fP,
fS, λP, λS e ∆t = tS - tP.
.
Substituindo a expressão para t0 encontrada no item a) na expressão da distância d percorrida pela onda S
temos:

λ p f p t p − λs f s t s 

d = vs  t s −


λ
f
λ
f
−
p p
s s 

Usando novamente a relação vs =λsfs e desenvolvendo a expressão acima temos:
d=
λ p f p λs f s
(t s − t p )
λ p f p − λs f
Ou seja:
d=
λ p f p λs f s
∆t
λ p f p − λs f
4
UFJF – MÓDULO III DO PISM – TRIÊNIO 2010-2012 – GABARITO DA PROVA DE FÍSICA
PARA O DESENVOLVIMENTO E A RESPOSTA DAS QUESTÕES, SÓ SERÁ ADMITIDO USAR CANETA ESFEROGRÁFICA AZUL OU PRETA
Questão 5 – Dois condutores esféricos, de raios r1 e r2, são separados por uma distância muito maior do que o
raio de qualquer uma das esferas. As esferas estão ligadas por um fio condutor, como mostra a figura abaixo. As
cargas nas esferas em equilíbrio são q1 e q2, respectivamente, e estão uniformemente distribuídas.
a) Calcule o potencial na superfície de cada esfera.
Como as esferas estão conectadas por um condutor temos:
V2 = V1 = K
q1
(para ambas esferas)
r1
b) Calcule a razão entre as magnitudes dos campos elétricos nas superfícies das esferas.
Devido ao fato das esferas estarem muito afastadas temos:
E1 =
1 q1
K
2 r12
E2 =
1 q2
K
2 r22
e
Dividindo uma expressão pela outra temos:
1
K
E1 2
=
E2 1 K
2
q1
r12 V1 r1
=
q2 V2 r2
r22
Como V2 = V1 temos:
E1 r2
=
E2 r1
5