Amplificadores

Instrumentação e Técnicas de Medidas
Revisão de Eletrônica – Amplificador Operacional
Controle de Versões
2010
Versão 1 – Instrumentação e Técnicas de Medidas (ITM)
2012
Versão 2 – Pequenas alterações no texto, links, CIs não obsoletos, capítulos 6 e 7
(interfaceamento, ruído, blindagem, aterramento).
2013
Versão 3 – Remoção dos capítulos 6, 7 (interfaceamento, ruído, blindagem,
aterramento) e filtros. União dos dois volumes originais em um só.
Versão 4 – Divisão do texto em vários módulos para serem revistos ao longo do
período. Neste módulo apenas Op. Amp. ideal e características DC e AC.
Última alteração: 28/08/2013
Instrumentação e Técnicas de Medida – UFRJ, 2013/2
Índice
4 Amplificador operacional ideal.........................................................................................................1
4.1 Introdução..................................................................................................................................1
4.2 O amplificador operacional real.................................................................................................1
4.3 Principais características do AO ideal.......................................................................................3
4.4 Símbolo......................................................................................................................................4
4.5 Equação e Modelo......................................................................................................................4
4.6 Configurações mais comuns:.....................................................................................................5
4.6.1 Amplificador inversor:.......................................................................................................5
4.6.2 Amplificador não-inversor:................................................................................................6
4.6.3 Amplificador somador:......................................................................................................8
4.6.4 Amplificador subtrator.......................................................................................................9
4.7 Problemas resolvidos...............................................................................................................10
1.1 Exercícios - AO ideal...............................................................................................................13
5 Características CC do amplificador operacional real......................................................................17
5.1 Corrente de polarização IB......................................................................................................17
5.1.1 Modelo para representar a corrente de polarização..........................................................18
5.2 Corrente de offset IOS.............................................................................................................18
5.2.1 Modelo para representar a corrente de offset...................................................................18
5.3 Tensão de offset VOS..............................................................................................................19
5.3.1 Modelo para representar Vos...........................................................................................19
5.4 Drifts de IB, IOS e VOS..........................................................................................................19
5.4.1 Tensão de offset...............................................................................................................20
5.4.2 Correntes de polarização..................................................................................................20
5.5 Ganho de malha aberta.............................................................................................................21
5.5.1 Ganho Diferencial............................................................................................................21
5.5.2 Ganho de modo comum...................................................................................................22
5.5.3 Modelo para ganho de modo comum...............................................................................23
5.6 Impedância de entrada.............................................................................................................23
5.7 Impedância de saída.................................................................................................................24
5.8 Limitação da tensão de saída...................................................................................................25
5.9 Rejeição a fonte de alimentação..............................................................................................25
Instrumentação e Técnicas de Medida – UFRJ, 2013/2
i
5.10 Modelo para Corrente Contínua:...........................................................................................26
5.11 Problemas resolvidos.............................................................................................................26
5.12 Circuitos para compensação de IB e VOS:............................................................................28
5.12.1 Compensação de IB no amplificador inversor...............................................................28
5.12.1.1 Caso do amplificador inversor................................................................................30
5.12.2 Compensação de VOS no amplificador não inversor....................................................32
5.13 Exercícios - AO Real.............................................................................................................33
6 Características em frequência do amplificador operacional real.....................................................39
6.1 Resposta em frequência e estabilidade....................................................................................39
6.1.1 Resposta em frequência não compensada........................................................................42
6.1.2 Resposta em frequência com compensação.....................................................................44
6.2 Características de desempenho em frequência.........................................................................46
6.2.1 Slew-rate..........................................................................................................................46
6.2.2 Settling time.....................................................................................................................47
6.2.3 Exemplo: Resposta em frequência...................................................................................47
6.3 Cargas Capacitivas...................................................................................................................51
Instrumentação e Técnicas de Medida – UFRJ, 2013/2
ii
4 Amplificador operacional ideal
4.1 Introdução
O circuito “amplificador operacional” (AO) nada mais é do que um amplificador com uma
saída e duas entradas, cujo modelo mais simples consiste de uma fonte de tensão controlada com
saída proporcional à diferença de tensão entre as entradas do AO. As características dos AO e a sua
utilização nos mais variados circuitos, muitos dos quais não lineares, são o alvo desta disciplina.
Internamente o AO é formado por um amplificador de elevado ganho obtido por meio de
múltiplos estágios acoplados diretamente. As duas entradas do AO são conectadas a um
amplificador diferencial. O elevado ganho de tensão força o uso de realimentação negativa para que
o AO trabalhe na região linear. Isto permite que o ganho dos circuitos amplificadores sejam
definidos apenas pela malha de realimentação. O acoplamento direto entre os estágios internos do
AO permite o seu uso de DC até frequências bem elevadas.
A origem do termo “operacional” vem dos antigos computadores analógicos, onde estes
amplificadores eram utilizados como elemento chave para a realização de operações matemáticas. O
nome “amplificador operacional” foi usado pela primeira vez em uma publicação de 1947, feita por
John Ragazzini, o qual descrevia as propriedades de circuitos capazes de amplificar a diferença
entre dois sinais analógicos. O artigo, que teve como base trabalhos anteriores, realizados entre
1943 e 1944, considerava as condições de realimentação linear e não-linear. Hoje em dia o AO é o
circuito integrado analógico mais utilizado.
Veja mais sobre história dos AO em Op Amp Application Handbook, Walt Jung, 2006.
4.2 O amplificador operacional real
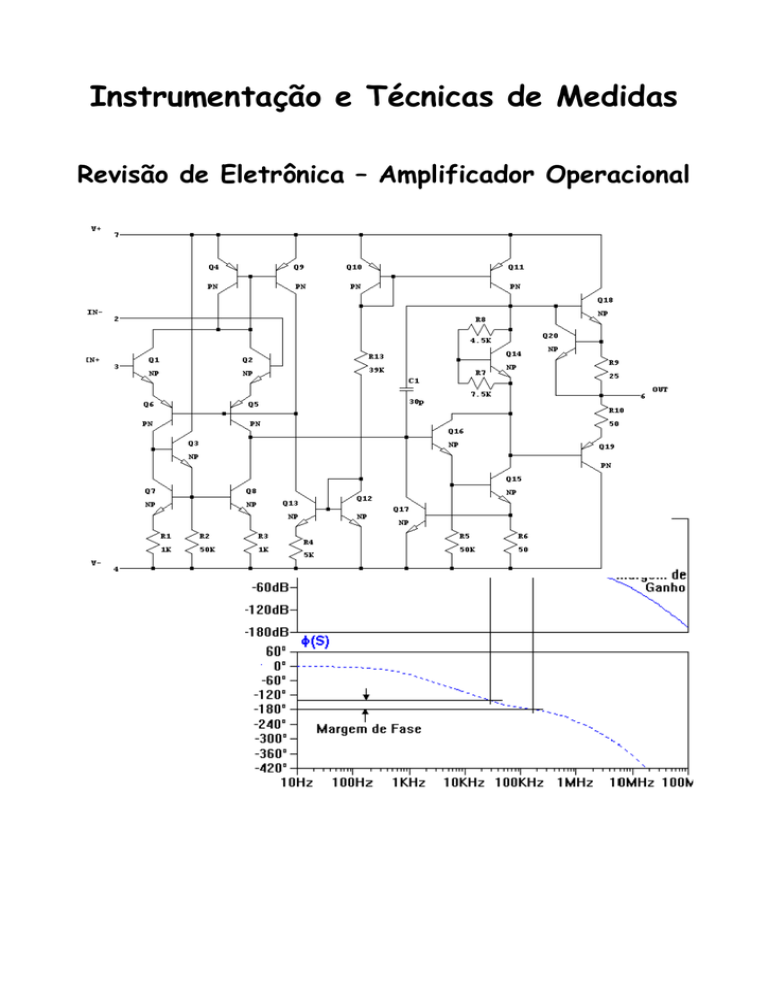
A Figura 4.1 mostra o esquema simplificado de um AO com três estágios de amplificação.
Nos circuitos atuais existem muito menos resistências, pois elas ocupam muito espaço no silício. No
lugar das resistências utilizam-se cargas ativas e espelhos de corrente produzidos com transistores.
O esquema da Figura 4.1 utiliza transistores bipolares de junção (TBJ) mas também existem
circuitos construídos com transistores de efeito de campo (FET).
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
1
+VCC
v–
vo
v+
–VCC
Figura 4.1: Esquema simplificado de um AO LM741, um AO de três estágios.
Cada um dos três estágios do amplificador da Figura 4.1 confere ao AO características
especiais:
1°estágio: par diferencial
•
apresenta alta impedância de entrada
•
responsável pelo elevado ganho diferencial
•
apresenta alta rejeição a tensões de modo comum
2°estágio: emissor comum
•
correção no nível DC para a saída
•
apresenta ganho de tensão elevado
3°estágio: seguidor de emissor (push-pull, classe B)
•
responsável pela baixa impedância de saída
•
apresenta alto ganho de corrente
•
responsável pela corrente de saída
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
2
4.3 Principais características do AO ideal
As principais características dos AO ideais são:
Característica
Símbolo
Valor
Notas
Ganho diferencial
Ad
∞
diferença entre as tensões nas entradas
Ganho de modo comum
Acm
0
tensão comum as duas entradas
Rejeição de modo comum
CMRR
∞
sinal comum as duas entradas
Impedâncias diferencial
Rid
∞
resistência entre as duas entradas
Impedância de modo comum
Ricm
∞
resistência de cada entrada para o terra
Impedância de saída
Ro
0
resistência de saída
Slew-rate
SR
∞
velocidade com que a saída pode variar
Settling time
ST
0
tempo de estabilização
Largura de banda
BW
∞
amplifica igualmente todas as frequências
Corrente polarização
Ib
0
para o par de transistores do primeiro
estágio
Corrente de offset
Ios
0
desigualdade entre as correntes I
Tensão de offset
Vos
0
diferença de tensão na entrada, necessária
para que a saída seja nula quando as
entradas forem nulas
Ruído elétrico
VN e IN
0
Variação de fase
φ
0
As características ideais de um AO nunca são alcançadas na prática, mas os erros
decorrentes de assumirmos estes valores ideais é pequeno. Desta forma é comum utilizarmos estas
características para simplificar a análise de circuitos com AO, como será mostrado nas seções
subsequentes.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
3
4.4 Símbolo
O símbolo mais comumente utilizado para representar um AO é apresentado na Figura 4.2.
Figura 4.2: Símbolos do AO, com e sem alimentação.
4.5 Equação e Modelo
Conforme descrito no início deste capítulo o modelo do AO pode ser visto na Figura 4.3.
Duas entradas de alta impedância comandando uma fonte de tensão controlada.
Figura 4.3: Modelo do AO ideal.
A tensão na saída da fonte é dada pela equação 4.1 e corresponde a amplificação da
diferença entre as tensões das do AO (entrada v+ e v-)
v O =Ad⋅v + −v − 
( 4.1 )
onde: Ad é o ganho diferencial do AO; v + e v − são as entradas do AO.
Se o ganho diferencial, Ad, é infinito, significa que v + =v − . Esta relação é válida sempre
que o AO está trabalhando na região linear. Trabalhar na região linear significa que existe
realimentação negativa sendo utilizada no AO, ou a diferença entre as tensões de entrada é tão
pequena que, mesmo com um elevado ganho diferencial, não ocorre a saturação do AO. Se
considerarmos o ganho Ad infinito (condição ideal) então para a saída ser um valor finito é
necessário que a diferença entre as entradas seja nula (condição ideal).
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
4
Sempre que o AO estiver saturado (saída igual a tensão de alimentação), então esta regra não
pode mais ser aplicada pois a equação 4.1 não é mais válida, ou seja, o operacional não está
trabalhando em uma região linear.
4.6 Configurações mais comuns:
4.6.1 Amplificador inversor:
A Figura 4.4 mostra o circuito básico de um amplificador inversor a base de AO.
Figura 4.4: Desenho básico de um amplificador inversor.
Se considerarmos o AO como ideal, o equacionamento do ganho fica muito facilitado pelo
uso de duas considerações:
1. Equacionar uma única corrente fluindo através de R1 e R2 e
2. Levar em conta que o potencial na entrada negativa é igual ao potencial na entrada
positiva (neste caso igual a zero).
A solução para o problema é a equação 4.2.
Como i 1 =
v 0 =−
vi
R1
e i 1 =−
v0
R2
, então
R2
v
R1 i
( 4.2 )
Por outro lado, se levarmos em conta que o ganho do AO não é infinito, devemos substituir
o desenho do AO pelo seu modelo ideal e isto nos leva a solução mostrada na equação 4.3.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
5
v −=
v i⋅R2 + v 0⋅R1
R1 + R 2
 v +−v − =
−
v0
Ad
=
v0
=−v − (pois a entrada positiva tem potencial zero)
Ad
v i⋅R 2 + v0⋅R1
R1 + R 2
v i⋅R2 + v 0⋅R1 =−
V 0 =−
v0
⋅ R1 +R 2 
Ad
R2
R +R
R1 1 2
Ad
⋅vi
( 4.3 )
Obs.: quando se considera Ad→∞ considera-se, implicitamente, que v+= v– pois esta é a
única forma de obter um vO finito.
A equação 4.2 mostra o resultado final do equacionamento, para ganho infinito. Resultado
idêntico pode ser obtido a partir da equação 4.3. Estas equações mostram que a rede de
realimentação determina o ganho do circuito amplificador, mesmo quando o ganho do AO não é
infinito. Convém notar, também, que a influência do ganho diferencial não infinito, é tanto menor
quanto menor for o ganho dado ao amplificador inversor.
Note, também, que apesar de a entrada inversora estar a um potencial igual zero, ela não esta
diretamente conectada a terra e não há circulação de corrente entre terra e este terminal. Por este
motivo, o terminal inversor, nesta configuração, é chamado de terra virtual.
4.6.2 Amplificador não-inversor:
A Figura 4.5 mostra o desenho básico de um amplificador não inversor formado por AO.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
6
Figura 4.5: Desenho de um amplificador não inversor básico.
Supondo que o AO seja ideal, a solução do problema é encontrada fazendo-se a tensão na
entrada negativa (divisor de tensão formado por R1 e R2) igual a tensão de entrada. Neste caso a
equação 4.4 é a solução do problema.
R1
⋅v = v
R1 + R 2 0 i
R1 +R2
R
⋅v i=1 2 ⋅vi
R1
R1
v 0=
v o R 1R2
R
=
=1 2
vi
R1
R1
( 4.4 )
Se considerarmos que o ganho do AO não é infinito, devemos substituir o desenho do AO
pelo seu modelo ideal e isto nos leva a solução mostrada na equação 4.5. Note que este circuito tem
realimentação negativa.
v + =v i
v −=
R1
⋅v
R1 +R2 0
v −v−=
vi −
v0
Ad
R1
v
⋅v 0 = 0
R1 +R 2
Ad
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
7
vo
 R1R 2⋅Ad
=
v i R 1R2R1⋅Ad
v 0=
R 1 + R2
⋅v
R 1 + R2 i
R1 
Ad
( 4.5 )
Podemos notar, nesta configuração, que se R1 =∞ ou R2 =0 então v 0 = v i . Neste caso o
circuito do amplificador não inversor é designado por buffer. O buffer possui ganho unitário e pode
ser utilizado para isolar estágios amplificadores, pois apresenta impedância de entrada infinita e
impedância de saída nula. Nota-se também que em ambos os casos, se o ganho Ad for considerado
infinito a solução para o problema é idêntica a obtida pela equação 4.4.
4.6.3 Amplificador somador:
A Figura 4.6 mostra a topologia do amplificador somador inversor básico implementado
com AO.
Figura 4.6: Circuito do amplificador somador inversor básico.
Como podemos observar, o amplificador somador consistir de uma série de amplificadores
inversores ligados em paralelo. Isto nos leva a aplicar a técnica de superposição de fontes, para
equacionar a tensão de saída deste circuito. Aqui também levamos em conta que o AO possui
características ideais de funcionamento, assim, a saída será dada pela equação 4.6 ou, no caso
particular de todas as resistências serem iguais, pela equação 4.7.
Supondo Ad → ∞ então v+= v–
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
8
i1=
v1
v2
v3
v0
, i2=
, i3 =
, i 4=−
R1
R2
R4
R4
i1 + i2 + i3 = i4
v 0 =- R4

v1 v2 v3
 
R1 R 2 R3

( 4.6 )
se R1=R2=R3=R, então a equação 4.6 pode ser reescrita conforme a equação 4.7.
vO=
−R4
⋅ v1 v 2v 3 
R
( 4.7 )
4.6.4 Amplificador subtrator
A Figura 4.7 mostra a topologia do amplificador subtrator básico implementado com AO.
Figura 4.7: Circuito do amplificador subtrator básico.
O cálculo torna-se mais cômodo se feito por superposição, utilizando-se o que já foi
calculado para o amplificador inversor e não inversor, aliado a consideração de que o AO é ideal. A
equação 4.8 mostra equação da tensão de saída deste circuito.
v 0=
R2
 v −v 
R1 2 1
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
( 4.8 )
9
4.7 Problemas resolvidos
Exercício 1: Dado o circuito abaixo, calcule sua função de transferência i L= f vi .
Considere os AO ideais.
a) Estabeleça valores para os resistores R, R 3 e R4 de forma que o circuito forneça uma corrente
máxima i L máx =1 mA para uma carga 0 ≤R L ≤10 K  quando v i =−10 V . Considere
R1 =R 2 =100 K  e V CC =±12 V .
b) Considere v i =0V . Calcule i L levando em conta a existência de uma fonte de tensão
conectada a entrada positiva de A1 e uma fonte de corrente conectada a entrada positiva de A2.
Solução:
Análise do circuito: A 2 : forma um amplificador de ganho unitário (buffer); A3 : forma um
subtrator junto com R3 ,R4 ; A1 : fornece a corrente de saída e é realimentado pelo subtrator através
de R1 ,R 2 .
Análise das realimentações de A1 : A1 recebe realimentação negativa (RN) através da
entrada não inversora de A3 e realimentação positiva (RP) através de A 2 e da entrada inversora de
A3 . Como o ganho dos dois caminhos do subtrator (entradas inversora e não-inversora) são iguais
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
10
em módulo, a RN é mais forte, porque a RP ainda passa pelo divisor resistivo R-RL. Como resultado
disto, o circuito possui realimentação negativa, o que permite o uso das técnicas estudadas.
Função de transferência:
R4
R⋅i L
R3
, logo
=0
R1 +R 2
v i⋅R2 +R 1
v −A =
1
i L=−
R2⋅R3
⋅v
R1⋅R 4⋅R i
a)
Sendo i Lmáx =1 mA e R Lmáx =10K então v L Imáx =10 V (tensão máxima na carga)
R=
v Omáx −v L Imáx
, onde V Omáx é a máxima tensão de saída do AO.
i Lmáx
Como V CC =±12 V, podemos limitar, co segurança, V Omáx =11V .
R=
11 V −10 V
=1K 
1 mA
Como i L=−
então
R4
R3
R2⋅R3
⋅v (a corrente independe de RL)
R1⋅R 4⋅R i
=−
R 2⋅v i
100 K −10 
=−
=10
Ri⋅R⋅i 0
100 K⋅1K⋅1m
assim podemos escolher, por exemplo, R 4=100K  e
R3 =10K 
b)
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
11
O problema pode ser calculado por superposição:
Efeito de VOS1:
v os1 =
R1 R4
⋅ ⋅R⋅i L
R1 +R2 R3
i L  v os1 =
 R 1 +R 2 ⋅R3
R1⋅R4⋅R
v os1
Efeito de IB2:
i L =i R −i b2

R4
R⋅i R
R3
−
vA =
=0
R1 +R 2
R1
1
i R=0
i L i b2 =−i b2
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
12
Portanto: i Ltot =
 R1 +R2 ⋅R3
v −i
R1⋅R 4⋅R os1 b2
4.8 Exercícios - AO ideal.
1) Determine os ganhos de tensão (vo/v1) e diga para que servem estas configurações
R 3 R4 R2 R3R 2 R4
v i , b) Esta configuração é empregada quando queremos
R1 . R 4
um alto ganho e não temos resistores de alto valor disponíveis para Req.
Respostas: a) v 0 =−
Respostas: a) Se R3=R2 então v 0 =
2R 2 R 2
⋅ 1 ⋅ v 2 −v 1  , b) amplificador subtrator com ganho
R1 R
ajustável por um elemento (R).
2) Calcule o ganho de tensão (vo/v1) para os circuitos a seguir e determine se os AO estão sob
realimentação negativa.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
13
3) Mostre que para o amplificador inversor e não inversor, o ganho pode ser escrito da seguinte
v o Ganho Ideal
R1
=
forma: v i
onde β=
1
R1+R 2
1
β⋅Ad
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
14
4) Ache a expressão de vo para o circuito abaixo em função de V1, V2 e Vcm.
5) Para o circuito em ponte mostrado abaixo, determine o valor da tensão de saída.
6) Calcule a corrente na carga RL para os dois circuitos a seguir. Considere R1=RF=R4=R5 e
RF=R2+R3
Resposta: i L =
vin⋅RF
R1⋅R3
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
15
Resposta: i L =−
vin⋅(R2+ R3)
R2⋅R3
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
16
5 Características CC do amplificador operacional real
As principais características CC dos AO reais podem ser encontradas em duas publicações
da Texas Instruments, SLOA011 e SLOA083, e outra da Analog Devices, Op Amp Basics.
5.1 Corrente de polarização IB
Essas são as correntes CC, necessárias em cada entrada do AO, para produzir zero Volts de
saída quando não há sinal em suas entradas. A corrente IB é a corrente de base dos transistores TBJ,
ou a corrente de fuga na porta dos FETs, utilizados no primeiro estágio de um AO. Para medir estas
correntes se utiliza um circuito simples conforme mostrado na Figura 5.1. Nesse circuito as
correntes de polarização são obrigadas a fluir sobre resistores de valor muito elevado (10MΩ ou
mais) produzindo uma tensão de saída mensurável. Os capacitores servem apenas como um filtro
passa baixas (0,01µF). As chaves S1 e S2 são abertas uma de cada vez para permitir a medida de I B1
e IB2.
Figura 5.1: Circuito para medida das correntes de polarização e offset.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
17
Essas correntes são da ordem de [µA] ou [nA] mas podem ser menores em AO com par
diferencial composto por uma configuração Darlington ou transistores FET. Nestes casos é possível
encontrar AO com IB da ordem de [fA].
5.1.1 Modelo para representar a corrente de polarização
A Figura 5.2 mostra o equivalente elétrico de um AO sujeito a influência de correntes de
polarização. Note que este esquema utiliza correntes diferentes para a entrada inversora e não
inversora.
Figura 5.2: Modelo equivalente para um AO em função de IB.
5.2 Corrente de offset IOS
Essa é a diferença entre as correntes de polarização das entradas positiva e negativa de um
AO. Como os componentes do amplificador de entrada não são exatamente iguais há uma pequena
diferença entre as correntes de polarização. Para medir esta corrente se utiliza o circuito da Figura
5.1 com as duas chaves abertas. Como as correntes de polarização são muito semelhantes e as
resistências muito elevadas é necessário que as resistências sejam casadas com tolerância da ordem
0,1% ou menos.
5.2.1 Modelo para representar a corrente de offset
O modelo para representação de IOS é o mesmo utilizado para IB (Figura 5.2). Em alguns
casos, quando temos apenas um valor para IB e outra para IOS, podemos calcular cada IB como
apresentado pela equação 5.1
IB = IB ± (IOS/2)
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
( 5.1 )
18
5.3 Tensão de offset VOS
Esta é a diferença de tensão CC, necessária na entrada de um AO, para produzir zero Volts
de saída quando não há sinal em suas entradas. A tensão de offset é causada pelo desbalanço do par
diferencial e pela desigualdade dos transistores do 2° estágio. Normalmente o valor da tensão de
offset é fornecido em módulo pois a tensão de saída pode ser afetada positiva ou negativamente.
Para facilitar a medida deste parâmetro utiliza-se um amplificador não inversor com entrada
aterrada e resistores de valores elevados, conforme mostrado na Figura 5.3.
Figura 5.3: Circuito para medida da tensão de offset.
5.3.1 Modelo para representar Vos
A Figura 5.4 mostra dois equivalentes elétricos de um AO com V OS. A fonte pode ser
colocada na entrada não inversora. A polaridade da fonte VOS não é definida pois a tensão de offset é
dada em módulo e sua polaridade pode mudar de operacional para operacional.
Figura 5.4: Modelos equivalentes para um AO em função de Vos.
5.4 Drifts de IB, IOS e VOS
Os drifts de IB, IOS e VOS correspondem as variações destes parâmetros com a temperatura,
tensão de alimentação, ou tempo. Estas variações ocorrem porque os componentes do circuito são
afetados de forma diferente por essas influências externas. Normalmente os valores de drift
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
19
correspondem a valores médios para um intervalo especificado de temperatura, tensão de
alimentação ou tempo.
5.4.1 Tensão de offset
As variações da tensão de offset com relação a temperatura, podem ser calculadas pela
equação 5.2.
V OS =V OS  25 ° C  
onde
dV OS
dT
dV OS
T
dT
( 5.2 )
é a deriva térmica.
Alguns amplificadores operacionais apresentam pinos externos que possibilitam o
balanceamento do par diferencial e, por consequência, o zeramento da tensão de offset (Figura 5.5).
Apesar deste recurso facilitar a compensação da tensão de offset ela causa um aumento na deriva
térmica de Vos.
Figura 5.5: Compensação da tensão de offset.
5.4.2 Correntes de polarização
As variações das correntes de polarização com relação a temperatura, podem ser calculadas
pela equação 5.3.
I B = I B  25o C 
Onde
dI B
T
dT
( 5.3 )
dI B
é a deriva térmica.
dT
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
20
Alguns manuais não citam a deriva térmica, para a corrente de polarização, mas indicam o
 T necessário para dobrar o valor de IB, o que já é o suficiente para utilizar a equação 5.3,
supondo que esta variação seja constante com a temperatura.
Tabela 5.1: Comparação entre drift de alguns AO
Amp. Op.
741C
CA3140
Tipo
TJB
FET
Fabricante
N.S.
Intersil
Analog Devices
Analog Devices
–
Vos
1
8
0,06
0,25(Máx)
mV
0,5
1,0(Máx)
µV/°C
drift/Vos
OP07C
AD547L
TJB alto desempenho FET alto desempenho
Unid.
–
IB
80
0,01
±1,8
0,01
nA
Ios
20
0,0005
0,8
0,002
nA
drift/Ios
0,018
nA/°C
5.5 Ganho de malha aberta
Da mesma forma que a impedância de entrada, o ganho de um AO pode ser dividido em
dois: Ganho diferencial (Ad) e de Modo Comum (ACM). Desta forma, o AO é classificado quanto a
sua habilidade de amplificar a diferença entre os sinais aplicados a suas entradas, e rejeitar a parcela
de sinal comum as duas entradas.
Além destas distinções feitas ao ganho dos AO, vale a pena ressaltar que os ganhos mudam
em função de uma série de itens como: a carga; a tensão de alimentação; a temperatura; outros
operacionais do mesmo tipo; ...
5.5.1 Ganho Diferencial
Este ganho é influenciado pelas características dos transistores do par diferencial de entrada
e sua carga. Se a fonte de corrente que alimenta o par diferencial apresentasse resistência infinita, as
variações de corrente em um ramo do amplificador diferencial seriam compensadas no outro ramo.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
21
Esse comportamento manteria constante a tensão de emissor, que no modelo de pequenos sinais
poderia ser considerado como aterrado. Desta forma o ganho de pequenos sinais do primeiro estágio
seria equivalente ao de um amplificador em emissor comum com emissor aterrado.
Normalmente o ganho diferencial dos AO é da ordem de 105 a 106 vezes.
5.5.2 Ganho de modo comum
Como a fonte de corrente que alimenta o par diferencial de entrada não apresenta resistência
infinita, mesmo aplicando sinais de mesma amplitude nas duas entradas do amplificador, as
correntes de coletor se alteram modificando a tensão de emissor. O modelo de pequenos sinais para
amplificador se torna um emissor comum com resistência de emissor. Por esta razão, o ganho para
sinais iguais nas duas entradas do amplificador é pequeno mas não nulo.
Nos manuais, uma informação importante é o fator de rejeição de modo comum, que é
definido como mostrado nas equações 5.4, 5.5 e 5.7.
CMRR=
Ad
(em valor absoluto)
ACM
CMRR=20⋅log
Ad =
 
Ad
ACM
(em dB)
Vo
V
= o
V + −V - V id
ACM =
( 5.4 )
( 5.5 )
( 5.6 )
Vo
V iCM
( 5.7 )
V +V 2
( 5.8 )
V iCM =
A Figura 5.6 mostra o circuito utilizado para medir o ganho de modo comum dos AO. Nesse
circuito um mesmo sinal é aplicado as duas entradas do AO sem realimentação. Com estas
informações, utiliza-se as equações 5.7, 5.4 e 5.5 para conhecermos a taxa de rejeição de modo
comum (CMRR). O CMRR nos AO é da ordem de 100dB.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
22
Figura 5.6: Circuito para medida do ACM dos AO.
5.5.3 Modelo para ganho de modo comum
A Figura 5.7 representa o equivalente elétrico de um AO quando levamos em conta o ganho
de modo comum.
Figura 5.7: Modelo equivalente para um AO em função de ACM.
5.6 Impedância de entrada
O primeiro estágio do AO é constituído de um amplificador diferencial cuja impedância de
entrada, apesar de ser muito elevada, não chega a ser infinita. Isto pode ser constatado pela simples
observação de que existem correntes de polarização fluindo para dentro do AO.
A impedância de entrada de um AO pode ser separada em duas outras impedâncias com
características bem distintas. Uma delas é a chamada impedância de modo comum (R icm), cujo efeito
é igual para as entradas inversora e não inversora. A outra impedância é chamada de diferencial
(Rid) e deve-se a características exclusivas de cada entrada (impedância entre as entradas).
A impedância diferencial é função das características da junção base emissor dos transistores
de entrada e da corrente de polarização destes. Sua influência pode ser quantizada por meio da
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
23
equação 5.9. No LM741, da Figura 4.1, esta impedância é da ordem de 2MΩ e nos operacionais, de
um modo geral, é de 107 até 1013Ω.
Rid ≈2⋅hie≈
2V T
IB
( 5.9 )
A impedância de modo comum é função da impedância de entrada da fonte de corrente, que
polariza o par diferencial, e do ganho de corrente deste. Esta impedância pode ser aproximada pela
equação 5.10. De um modo geral esta impedância é da ordem de 107 até 1013Ω.
Ricm =
hfe
hoe
( 5.10 )
Para mais informações veja Sedra/Smith, Microeletrônica, Makron Books, 2005 ou procure
na internet por Jaeger/Blalock, Analog Integrated Circuits, em Microelectronic Circuit Design, Mac
Graw-Hill, 2003.
5.7 Impedância de saída
Esta impedância se deve principalmente às impedâncias de saída do 2°estágio (hoe–1),
refletidas para a saída do AO, e pode ser representada por um resistor série, colocado na saída dos
AO.
A resistência de saída (Ro) influencia no cálculo do amplificador realimentado porque o
ganho do amplificador em laço aberto não é infinito. Assim, a realimentação não consegue corrigir
totalmente a queda de tensão na resistência de saída Ro. Tipicamente a resistência de saída é da
ordem de 50  e em aplicações de precisão não devemos drenar mais do que 2 ou 3 mA da saída
do AO.
A Figura 5.8 mostra um amplificador inversor completo, onde a resistência de saída (Ro) do
AO é levada em conta. Note que a tensão de saída passa por um divisor de tensão formado por Ro e
RL e que Ro também influencia na malha de realimentação.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
24
Figura 5.8: Amplificador não inversor com Ro não nula.
Considerando Ro na topologia do amplificador não inversor, a tensão de saída fica
modificada de acordo com a equação 5.11.
vo=
RL //  RRf 
⋅vo '
RoRL //  R+Rf 
( 5.11 )
Comparando o ganho desse circuito com o ganho ideal da configuração não inversora se
nota que o ganho da configuração ficou reduzido de:
1
Ro
Ro
1

RL RRf
5.8 Limitação da tensão de saída
Com exceção aos amplificadores chamados rail to rail a tensão de saída dos AO nunca
alcança a tensão de alimentação. Isso se deve a quedas de tensão sobre os transistores do 2° e 3°
estágios de amplificação.
5.9 Rejeição a fonte de alimentação
A polarização dos transistores é dependente da tensão de alimentação utilizada e isso faz
com que o AO não seja imune às variações de tensão na alimentação. O fator que caracteriza esta
imunidade é chamado de rejeição a fonte de alimentação (Power Supply Rejection) e pode ser
calculado pelas equações 5.12 ou 5.13.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
25
PSRR=
V O
(em valor absoluto)
V CC
PSRR=20⋅log
 
VO
 V CC
(em dB)
( 5.12 )
( 5.13 ).
Valores típicos para PSRR dependem da qualidade do AO: para o 741C a PSRR é de
±30mv/v enquanto que para o OP27A a PSRR é de 0,2mv/v.
5.10 Modelo para Corrente Contínua:
Os modelos apresentados individualmente para representar IB, IOS, VOS, A, Rid, RCM, RO e
outros podem ser agrupados em um só modelo como mostra a Figura 5.9.
Figura 5.9: Modelo equivalente para um AO em função de: IB, Ios, Vos, A, Rid, Ricm, Ro.
5.11 Problemas resolvidos
Para o circuito da Figura 5.10, considerando VOS1 e VOS2 diferentes de zero e Ad1 e Ad2
finitos:
a) Calcular Vo em função destes parâmetros e dos resistores.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
26
b) O manual da Analog Device, que apresenta este problema, informa que A2 deve ter
baixo VOS para o bom funcionamento do circuito. A influência de V OS2 é realmente significativa?
Precisamos realmente ter um A2 de boa qualidade?
Figura 5.10: Circuito para o problema resolvido.
Solução
a)
Figura 5.11: Adaptação do circuito da Figura 5.10 levando em conta os efeitos de Vos.
Para A1 :
V O1 =Ad1⋅V d1
V d1=V X −V OS1
V O1 =Ad1⋅V X −V OS1 
Para A2
V O =Ad2⋅V d2
V d2V O1V OS 2 =0
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
27
V d2=−V OS2−V O1
V O =−Ad2⋅ V OS2  Ad1 V X −V OS1 
Pela malha de realimentação podemos dizer que
V X=
R1
⋅V
R1 R2 O
Assim
−
VO
Ad2

=V OS2 Ad1⋅
R1
⋅V −V OS1
R1R 2 O

Isolando VO, temos:
V OS1−
V O=
R1
R1 R2

V OS2
Ad1
1
Ad1⋅Ad2
Nota-se na expressão de VO, que a influência de VOS2 é muito menor que a de VOS1, pois a
primeira aparece dividida por Ad1, que tem um valor muito elevado. Assim, conclui-se que A 2 não
precisa ser tão bom quanto indicava o artigo da Analog Devices.
5.12 Circuitos para compensação de IB e VOS:
5.12.1 Compensação de IB no amplificador inversor
O modelo que representa os efeitos das correntes de polarização sobre um amplificador
inversor é apresentado na Figura 5.12. Por esta figura fica claro que a corrente IB- circula pela malha
de resistores ao passo que a corrente IB+ é curto circuitada. Este circuito pode ser calculado por
superposição.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
28
Figura 5.12: Modelo de amplificador inversor sob influência das IBs.
Para Vin=0 (as duas extremidades do resistor R1 estão conectados a potencial zero)
V O1=R2⋅I B −
Para IB– = 0
V O2=
−R2
⋅V in
R1
Logo
V 0=
−R2
⋅V inR 2⋅I B −
R1
Parte da tensão de saída é função da corrente de polarização. Este erro introduzido na tensão
de saída pode ser reduzido pela inclusão de um resistor, R3, entre a entrada não inversora e o terra.
Para IB+ = 0 e IB– = 0
V 01 =
−R 2
V
R1 in
Para IB+ = 0 e Vin = 0
V O2=R 2⋅I B −
Para IB– = 0 e Vin = 0
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
29
V O3=
R1R2
⋅R3⋅I B 
R1
Logo
V0=
−R 2
−R3
⋅V i R2⋅I B − 
⋅ R1 R 2 ⋅I B
R1
R1
Supondo I B + = I B − =I B
V 0 =-
R2
R1
V i I B  R2 −
R3
R1
 R1 R2 
Para que o segundo termo da equação seja nulo
R2 −
R3
⋅ R1R 2 =0
R1
 R1 R2 
R3⋅
= R2
R1
R3 =
R 2 R1
R1R 2
A diminuição dos efeitos de IB podem ser compensadas com a inclusão de um resistor
conectado entre a entrada positiva e o terra, R3, de valor R1 // R2. Quando isto acontece a saída
depende apenas da entrada e da rede de realimentação R1 e R2.
5.12.1.1 Caso do amplificador inversor.
Observa-se pela Figura 5.13, independente do modelo utilizado, que a tensão V OS afeta a
saída como se fosse aplicada sobre um amplificador não inversor.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
30
Figura 5.13: Dois modelos para o amplificador inversor sob influência das Vos.
Resolvendo por superposição temos
V O=
−R2
 R R 2
⋅V in  1
⋅V OS
R1
R1
Sendo assim, é possível somar ou subtrair tensões para remover a parcela da saída
dependente de VOS. Um dos circuitos para remover este offset é apresentado na Figura 5.14.
No circuito da Figura 5.14 foram adicionadas resistências a entrada positiva do AO. Estas
resistências alteram o circuito transformando o amplificador inversor em um subtrator. A tensão Vin
continua sendo amplificada como em um amplificador inversor, porém soma-se (ou se subtrai) a
esta, uma parcela obtida pela tensão Vx aplicada ao amplificador não inversor. Se P1 for ajustado
para fazer Vx igual a VOS a tensão de offset é compensada. Valores de referência positivos e
negativos são utilizados nos extremos de P1 para permitir a compensação de tensões de ambos os
sinais.
Para ajudar na compensação de IB, as resistências podem ser escolhidas de tal forma que
*
R1 // R2=R3 R4 //  R5P 1 
A resistência de P1, vista pelo circuito, varia com o ajuste do potenciômetro e isto altera a
impedância total da malha vista pelo AO. Para minimizar estes efeitos se utiliza R5>>R4.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
31
Figura 5.14: Amplificador inversor com correção da tensão de offset.
5.12.2 Compensação de VOS no amplificador não inversor.
Uma alternativa para corrigir o efeito da VOS na configuração não inversora, sem reduzir a
impedância de entrada da configuração, é apresentada na Figura 5.15.
Este circuito, muito semelhante ao utilizado na configuração inversora, modifica o ganho do
amplificador pois uma resistência variável R3+P1 é colocada em paralelo com R1. Para minimizar
estes efeitos se utiliza valores de R3 e P1 tais que as alterações em P1 modifiquem minimamente o
valor da resistência equivalente
*
R1≈R1 //  R3P 1.
Figura 5.15: Amplificador não inversor com circuito para compensação de offset.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
32
5.13 Exercícios - AO Real.
1)
No circuito abaixo:
a) Calcule R1 para que a saída fique centrada em 0V.
b) Qual o valor de R2 para que o amplificador tenha mínimo erro devido a IOS.
2)
No circuito abaixo determine VO em função de Vi, considerando também VOS, IOS e Ad
Para este amplificador considere: VOS =2mV; IB =100nA; IOS =20nA; Ad =10.000;
3)
Para a configuração amplificador subtrator:
a) Calcule VO levando em conta VOS, IB+, IB-, e Rid.
b) Calcule Vo considerando Ad e CMRR finitos.
c) Verifique qual o CMRR do circuito em função do CMRR do amplificador operacional.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
33
4)
O circuito abaixo foi testado sob três condições diferentes.
Testes:
1 – Vi=0; R1=10K; R2=390K; R3=0; VO = 497,5mV
2 – Vi=0; R1=10K; R2=390K; R3=33K; VO = 299,5mV
3 – Vi=0; R1=39K; R2=390K; R3=0; VO = 207,5mV
Perguntas:
a) Calcule VOS, IB+, IB– e IOS.
b) Calcule VO para o teste “2” mas com Vi = 10mA
5)
Para um AO com resistência de entrada diferencial (R id) finita, com resistência de saída (RO) maior
que zero e com ganho (Ad) finito, calcule Av, Ri e Ro para a configuração não inversora.
6)
Para um buffer e um amplificador inversor de ganho unitário: verifique a influência do ganho de
modo comum e do CMRR em cada uma das configurações.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
34
7)
No circuito a seguir os amplificadores operacionais são reais e absolutamente iguais. Foram feitos
os seguintes testes com o circuito:
a) Com as chaves Ch1, Ch2 e Ch3 fechadas e Vi = 0: VO = -2mV.
b) Com a chave Ch3 fechada, as chaves Ch1 e Ch2 abertas e Vi = 100mV: VO = -4.89V
c) Com as chaves Ch2 e Ch3 abertas, Ch1 fechada e Vi = 0: VO = 0;
Pergunta:
Calcular IB, VOS e CMRR com as respectivas polaridades. Considere as outras características do
amplificador operacional se aproximando do ideal. Fazer os cálculos com precisão de 1mV para
tensão e de 1nA para corrente. Suponha chaves ideais.
8)
Calcule a impedância de entrada do circuito abaixo. Utilizando apenas resistências e/ou
capacitâncias para Z1, Z2, ..., Z5, como poderíamos simular um indutor?
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
35
9)
Equacione o circuito abaixo e explique por que esta configuração possibilita um aumento na
impedância de entrada da configuração não inversora. Considere os amplificadores operacionais
com comportamento real e constituídos na mesma pastilha (AO idênticos). Use o ganho tendendo a
infinito e as correntes de polarizações iguais.
OBS.: A impedância de entrada é dada por Zin = Vin/Iin. Compare este circuito com o não inversor.
10)
Supondo ganho finito para o amplificador operacional, calcule a impedância de saída da seguinte
configuração.
11)
Qual o ganho real na configuração inversora se o resistor de realimentação é 5MΩ, o resistor de
entrada é 10KΩ, o ganho diferencial é 80dB, a impedância de entrada do operacional é 300KΩ e a
resistência de saída do operacional é 100Ω. Calcule também a impedância de entrada e de saída do
circuito completo.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
36
12)
No circuito abaixo foram realizadas as seguintes medidas:
a) S1 e S2 fechadas:
VO = 0,04V
b) S1 aberta e S2 fechada: VO = 0,1V
c) S2 aberta e S1 fechada: VO = -0,06V
Calcule IB+, IB– e IOS.
13)
Admitindo que o AO do circuito abaixo seja um 741 típico (V os(típico) = 2mV; IB(típico) = 80nA;
Ios(típico) = 20nA; Ad(típico) = 200.000):
a) determine a resistência de entrada do circuito.
b) determine a expressão de VO levando em conta VOS, IOS, Ad. Compare com o AO real.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
37
14)
Calcular a função de transferência supondo a existência de IB+, IB–
amplificadores:
e VOS para os seguintes
a) inversor (com um resistor R3 ligado entre a entrada V+ do AO e terra):
b) não-inversor (com um resistor R3 ligado entre Vi e a entrada V+ do AO):
15)
Calcular a função transferência supondo a existência de CMRR para os seguintes amplificadores:
a) inversor;
b) não-inversor;
c) buffer:
CMRR= 90dB, Ad = 200.000
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
38
6 Características em frequência do amplificador operacional real
6.1 Resposta em frequência e estabilidade
Em um amplificador realimentado, como no caso dos circuitos com AO, tanto o
amplificador quanto a malha de realimentação costumam ser modelados por ganhos, conforme
indicado na Figura 6.1. O ganho do elemento amplificador é chamado de ganho em laço aberto – no
AO este ganho corresponde ao A d(S). O ganho da malha de realimentação é chamado de β(S). Bons
textos são Feedback, Op Amps and Compensation, da Intersil, Op Amp for Everyone (capítulos 5, 6
e 7), Texas Instruments,
Vi
+
_
Ad(S)
Vo
β(S)
Figura 6.1: Diagrama em blocos de um amplificador realimentado.
Pelo diagrama em blocos deve ser claro que
V O S = Ad  S ⋅ V i  S  – V O S ⋅S  
e, portanto que a equação 6.1, representa o ganho do amplificador realimentado ou o ganho
de malha fechada.
V O S 
Ad S 
=AV S =
V i S 
1 Ad S ⋅S 
( 6.1 )
O ganho Ad(S) é constante para CC mas a partir de uma determinada frequência começa a
decair. O ganho β(S) pode ser constante ou apresentar comportamento variável com a frequência.
Em baixas frequências, normalmente, os dois ganhos são constantes e o denominador da
equação 6.1 é positivo e maior do que 1. Isto garante a estabilidade da função de transferência. Se o
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
39
ganho Ad(S) for muito elevado, como nos casos do AO, o ganho da malha de realimentação, β(S), é
responsável pelo ganho do amplificador realimentado (equação 6.2).
V O S  1
=
V i S  
( 6.2 )
Em altas frequências a estabilidade depende do comportamento de Ad(S) e β(S). Por esta
razão é comum estudar separadamente o comportamento do chamado ganho de malha, ou seja do
produto L S = Ad S ⋅S  .
Se, em alguma frequência, a fase do ganho de malha for 180º, então o ganho de malha será
negativo. Se, cumulativamente, o módulo do ganho de malha for unitário, o ganho do amplificador
torna-se infinito ( 1 Ad S ⋅S =0 ). Esta é uma situação limite de estabilidade que corresponde a
colocar os polos do amplificador realimentado sobre o eixo jω. Se o módulo do ganho de malha
aumentar (mantendo a fase em 180º), os polos do amplificador realimentado deslocam-se para a
direita do eixo jω ( 1 Ad S ⋅S 0 ). Em síntese: se o ganho de malha for ∣1∣∢180o o circuito
torna-se um oscilador e se o ganho de malha for maior do que ∣1∣∢180 o o circuito torna-se
instável.
Uma análise preliminar indica que não existe problema de instabilidade para amplificadores
realimentado com 1 ou 2 polos, pois a fase do ganho de malha nunca será 180º. Para amplificadores
realimentados com 3 ou mais polos, o problema da instabilidade não pode ser esquecido.
O diagrama de Bode do ganho de malha, Figura 6.2, pode ser utilizado para simplificar a
análise da estabilidade dos amplificadores realimentados. Neste diagrama de Bode, são desenhados
os gráficos de módulo e fase do ganho de malha, representado conforme equação 6.3. O gráfico,
apesar de simples, utiliza escala logarítmica de frequência e ganho em dB.
Ganho em dB
corresponde a 20⋅log∣Ganho Linear∣ . Ganho unitário corresponde a 0dB. Ganho em dB negativo
equivale a ganho linear com módulo entre 0 e 1. Ganhos de 20⋅log X  correspondem a
−20⋅log 1/ X 
Ad  j ⋅ j =∣Ad  j ⋅ j ∣⋅e
j⋅ 
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
( 6.3 )
40
Figura 6.2: Diagrama de Bode do ganho de malha de um amplificador realimentado.
A estabilidade está garantida se, no diagrama de Bode do ganho de malha, para a frequência
onde a fase é 180º, o módulo do ganho for menor do que 1 (valor menor do que 0dB). Da mesma
forma, se para a frequência de ganho unitário, a fase de Ad S ⋅S  for maior do que –180º (-150º,
–120º... ), o amplificador também é estável.
Neste diagrama de Bode é possível identificar duas figuras de mérito importantes: a margem
de ganho e a margem de fase. A diferença entre o valor do ganho para a fase de –180º e o ganho
unitário é chamado de margem de ganho (equação 6.4). A diferença entre a fase para ganho unitário
e –180º é chamado de margem de fase (equação 6.5).
MG[dB ]=−∣Ad  S ⋅ S ∣=−180
( 6.4 )
MF [graus]=180 o−∣∣∣Ad  S ⋅ S ∣=0dB
( 6.5 )
o
Partindo-se desta análise é possível concluir que o amplificador realimentado representado
pela Figura 6.2 é estável. Observa-se que para ganho unitário (0dB), a fase é menor do que –180º
(-150º). De outra maneira, quando a fase é –180º o módulo do ganho de malha é menor do que um
(menor do que 0dB).
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
41
Quando o ganho dos AO não pode ser alterado só resta alterar a rede de realimentação para
garantir a estabilidade do amplificador em malha fechada. A determinação de um ganho de
realimentação que deixe estável o circuito pode ser obtida da seguinte forma: 1) desenha-se o
diagrama de Bode para Ad(S) (Figura 6.3), 2) determina-se uma margem de fase considerada
aceitável, 3) determina-se o ganho do AO para a frequência onde a margem de fase é atendida. 4)
determina-se o ganho de realimentação de tal forma que β–1 = Ad. Este valor de Ad corresponde ao
menor ganho da configuração realimentada e que atende ao requisito de mínima margem de fase,
pois ∣Ad S ⋅S ∣=1 .
No exemplo da Figura 6.3, para que a margem de fase do amplificador realimentado seja da
+45º, ajusta-se o ganho de realimentação de tal forma que ∣AS ⋅ S ∣=1 , para a frequência onde
a fase do AO corresponde a –135º. Como, neste ponto, o ganho do AO corresponde a 60dB, o ganho
β corresponde a –60 dB (no gráfico isto corresponde a reta denominada 20⋅log1/=60dB ). Se
for escolhido um ganho β maior, –30dB, por exemplo, o ganho de malha será ∣1∣∢−180o .
Figura 6.3: Diagrama de Bode do ganho de malha de um amplificador realimentado.
6.1.1 Resposta em frequência não compensada
Cada estágio do amplificador operacional é composto por transistores que definem
diferentes polos. Na maioria das vezes estes polos estão distantes, de modo que alguns se tornam
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
42
dominantes. Estes polos dominantes limitam a resposta em frequência dos estágios, e por
conseguinte, do amplificador operacional como um todo. Para CC e baixas frequências o ganho é
praticamente constante, para altas frequências o ganho diminui com a frequência. A Figura 6.4
mostra a influência de três polos dominantes, um de cada estágio de um AO típico.
Figura 6.4: Resposta em frequência de cada estágio de um típico AO não compensado.
A equação 6.6 corresponde ao ganho do sistema não compensado, mostrado na Figura 6.4.
p 1⋅p 2⋅p 3
Ad S = Ad0⋅
 S p1 ⋅ S p 2⋅S  p 3
( 6.6 )
onde Ad0 é o ganho em baixas frequências, Ad(S) é o ganho de tensão em laço aberto, p 1, p2,
e p3 são os polos.
Os efeitos individuais dos polos de cada estágio do AO foram somados para montar o
gráfico da Figura 6.5. Observa-se que o AO tem ganho de 29dB na frequência onde a fase é – 180º.
Sendo assim este AO será estável em todas as configurações com ganho maior do que 29dB, caso
contrário o circuito se torna um oscilador.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
43
Figura 6.5: Resposta em frequência de um típico AO não compensado.
Por esta razão alguns AO de banda larga (amplificadores desenvolvidos para operar em
frequências elevadas) só podem ser utilizados em configurações com ganho mínimo estabelecido
pelo fabricante. Muitas vezes estes operacionais não são estáveis para ganho unitário. Como
exemplo disto temos o LF357, que é estável em configurações com ganho maior do que 5.
6.1.2 Resposta em frequência com compensação
Para corrigir a resposta em frequência de um AO (instabilidade ou resposta a transitórios)
emprega-se algum tipo de compensação. Esta pode ser externa (AO antigos de banda larga e alto
desempenho – LM301, LM308, ...) ou interna (AO de propósito geral - LM741, LF351, LM318 ...)
ao AO.
Uma forma de compensar o AO, para permitir a sua estabilidade em um determinado ganho
de malha fechada consiste em introduzir um polo de baixas frequências, de modo que a nova
resposta em frequência do AO intercepte a curva 20⋅log (1/β) com inclinação de -20dB/déc (curva
Ad(S) compensada Figura 6.6). Este comportamento, infelizmente, introduz um polo adicional em
frequência muito baixa o que diminui sensivelmente o ganho do AO em todas as frequências. Isto é
prejudicial ao desempenho global do AO pois seu comportamento ideal apresenta ganho elevado
para todas as frequências.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
44
Figura 6.6: Compensação de um AO com um polo dominante.
A diminuição no valor do primeiro polo do AO também pode ser utilizado para estabilizar o
amplificador realimentado sem introduzir um polo adicional. Como vantagem o método permite
ganhos maiores para todas as frequências. Como desvantagens é necessário capacitores de valor
elevado dentro do AO.
No LM741 é utilizada uma técnica alternativa e muito comum para compensação. É incluído
um pequeno capacitor (≈30pF) entre a base e o coletor de algum transistor do 2° estágio. O efeito
deste capacitor é multiplicado pelo ganho do 2° estágio (efeito Miller) e refletido para a saída do 1°
estágio. Isto faz com que seja criado, no 1° estágio, um polo em uma frequência muito baixa
(≈10Hz), um zero na frequência de p2 e outro polo em uma frequência bastante elevada (≈1MHZ).
Em suma, p2 é cancelado, e p1 é deslocado para direita. O resultado final é de um amplificador com
comportamento de um único polo em quase toda a faixa de frequência.
No caso do LM741 é possível considerá-lo como um circuito de um único polo até a
frequência de 1MHz (p3), conforme indicado na equação 6.7. Acima desta frequência o ganho em
malha aberta é menor do que 1 (0dB), e isto garante a estabilidade do AO até mesmo para ganho
unitário. O custo desta estabilização foi a redução da largura de banda do AO (largura da faixa de
passagem).
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
45
AV  S =
A0⋅p1 A0⋅p 1 GBW
≃
=
S  p1
S
S
( 6.7 )
onde GBW é o produto ganho faixa do AO
Nesta aproximação o GBW é constante, ou seja, se o ganho de malha fechada for diminuído
há um aumento proporcional na faixa de frequências que pode ser amplificada por este ganho.
6.2 Características de desempenho em frequência
Além do ganho do amplificador em malha aberta e do produto ganho faixa existem outras
características que determinam o desempenho dos AO com relação a frequência.
6.2.1 Slew-rate
O slew-rate (SR) representa a máxima variação de tensão (  V O ) que um amplificador
operacional pode apresentar, na saída, em um dado intervalo de tempo  T . A principal causa de
limitação do slew-rate é a resposta em frequência do AO e, principalmente, o polo dominante.
Valores típicos para o slew-rate vão de 1V/µs, em amplificadores de uso geral, à 2000V/µs em
amplificadores rápidos. O valor típico de SR para um LM741 é de 0,5V/µs e para o LM748 é de
40V/µs.
Para medir o slew-rate utiliza-se um buffer (amplificador não inversor de ganho 1) e um
gerador de funções. O gerador aplica uma onda quadrada na entrada do buffer. O sinal de saída é
medido conforme o indicado na Figura 6.7. Para o cálculo do SR utiliza-se o menor valor obtido
pelas equações 6.8 e 6.9.
Figura 6.7: Resposta do AO para uma entrada em degrau. Medidas para determinação do
SR.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
46
SRS =
90 %⋅Vmáx −10 %⋅Vmáx
ts
( 6.8 )
SRD =
90 %⋅Vmáx−10 %⋅Vmáx
td
( 6.9 )
onde SRS é o slew-rate de subida, SRD é o slew-rate de descida.
6.2.2 Settling time
É o tempo necessário para que a resposta do AO, a uma entrada em degrau, estabilize dentro
de uma faixa de valores considerada aceitável. Esta faixa de valores normalmente corresponde a 0,1
ou 0,01% por cento do valor final.
Dependendo das características do amplificador operacional, da rede de realimentação e da
compensação, o circuito apresentará um determinado grau de amortecimento (ζ → zeta: constante
de amortecimento), podendo ser considerado sobre, sub ou criticamente amortecido. Assim a saída
levará algum tempo para se acomodar no valor de regime estacionário, devido ao transitório. Este
intervalo de tempo é definido como tempo de acomodação ou settling time. A Figura 6.8 mostra
como identificar o tempo de acomodação de um sistema a partir de uma excitação em degrau.
Figura 6.8: Tempo de acomodação da saída de um AO após uma entrada em degrau.
6.2.3 Exemplo: Resposta em frequência
Para o circuito abaixo considere que os dois AO têm características dinâmica do tipo polo
dominante. Deseja-se que o circuito apresente um polo em 100kHz (devido a A1) e outro em 1MHz
(devido a A2). Determine o produto ganho faixa (GBW) de cada um dos AO para que esta
especificação seja atendida.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
47
O circuito deve fornecer uma saída VO senoidal de até 100kHz e com 10V p sem distorcê-la.
Calcule o slew–rate (SR) mínimo de cada AO para atender a esta especificação.
Considere o modelo CC dado abaixo. Calcule a tensão de saída V O para Vi=0, em função de
VOS1, Ad1, VOS2, Ad2 e dos resistores. Um dos AO tem mais influência sobre este valor de VO? Qual?
Solução.
Os dois AO estão funcionando com realimentação negativa portanto estão em uma região
linear.
a) Em um amplificador realimentado, com polo dominante, o diagrama de Bode de um
amplificador corresponde a uma reta com inclinação –20dB/década. O ponto de funcionamento do
circuito realimentado corresponde a interseção deste gráfico com a reta 20⋅log1/  . Desta
maneira só precisamos igualar as duas funções:
O ganho de malha aberta de A2 é
A 2  S =
GBW 2 GBW 2
≃
S  p2
S
O ganho em malha fechada de A2 deve ser
GBW 2
1
=
f
 f 
∣ ∣
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
48
Determinação do ganho da rede de realimentação.
Considerando Ad não infinito, a configuração inversora apresenta ganho igual a
v 0 =−
R4
v o Ganho Ideal
⋅v i
R3
=
R3 +R 4
, ou v i
onde β=
1
R3+R4
1
R 3
β⋅Ad
Ad
Reescrevendo as equações temos
Ad⋅⋅R4
vo
R3
=
v i 1β⋅Ad
Ad⋅R4
vo
R R 4
= 3
v i 1 β⋅Ad
logo o fator β corresponde ao ganho de realimentação.
Assim
1 R3 R4
=
R3

GBW 2 =
R3 R4
10 k 100 k
⋅ f 2=
⋅1 MHz=11 MHz
R3
10 k
O ganho de malha aberta de A1 é
A1  s =
GBW 1
S  p1
≃
GBW 1
S
e o ganho em malha fechada de A1 deve ser
GBW 1
1
=
f
 f 
∣ ∣
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
49
Assim
1 R 1R 2 1
1 k 100 k 1
=
⋅ =
⋅ =10 ,1
R1
AV2
1k
10

1
GBW 1= ⋅f 1=10 ,1⋅100 kHz=1, 01 MHz

b) Para A2:
 
SR2 ≥
dV O
dt
=
máx
d
 10⋅sen  2π f ⋅t ∣t=0
dt
SR2 ≥10⋅2⋅⋅ f ⋅cos 2π f ⋅t∣t =0=10⋅2π⋅100. 000
SR2 ≥ 6,283V/µs
Para A1:
Devido ao ganho de A2, a saída de A1 necessita ter apenas 1/10 da amplitude de V O, SR1 ≥
0,6283V/µs
c)

v O1= Ad 1⋅ V OS1
R1
⋅v
R1 R2 O

Instrumentação e Técnicas de Medida – UFRJ, 2013/1
50
V OS2 −
v O v O1⋅R4 vO⋅R3
=
Ad 2
R3R 4
Substituindo uma equação na outra
R3 R 4 V OS2
⋅
−V OS1
R4
Ad 1
vO =
R3 1
R R 4
R1
1
⋅
 3
⋅

R 4 Ad 1
R4
Ad 1⋅Ad 2 R1 R2
Levando-se em conta que os ganhos diferencias Ad são elevados,
v O ≃−
R1 R2
⋅V OS1
R1
Observa-se que VOS1 é predominante.
6.3 Cargas Capacitivas
Em um AO uma carga capacitiva pode alterar a impedância de saída equivalente e introduzir
mais um polo no ganho de tensão de malha aberta. Como resultado é possível que o circuito se torne
instável, pois o polo retira fase do sistema e aumenta em 20dB/dec a atenuação do ganho de malha
aberta a partir dele. Se a curva 20⋅log 1/ interceptar a curva de ganho em malha aberta depois
da frequência de corte inserida pela carga capacitiva o circuito pode se tornar instável. O polo
induzido por esta carga pode ser determinado pela equação 6.10
p CL=
1
RO⋅C L
( 6.10 )
mas sua determinação não é fácil, pois RO é função da frequência. Normalmente cargas
capacitivas aparecem em malhas de compensação externa, desacoplamentos, filtros, na excitação de
algum transdutor, LCD, ou quando a carga está conectada ao AO por fios muito longos, como uma
linha de transmissão, sistemas de áudio, vídeo, RF e outros. Neste último caso, a carga capacitiva
limita a transmissão de dados em velocidades elevadas.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
51
Via de regra AO de uso geral toleram cargas capacitivas de até 1000pF enquanto que para
AO de alta frequência a carga capacitiva deve ser limitada a uns 25pF. Quando se trabalhar com
cargas deste tipo se deve utilizar amplificadores com baixa impedância de saída, ou prover uma
redução desta impedância utilizando um amplificador de reforço de corrente. Para o caso da linha de
transmissão o reforço de corrente pode ser muito importante, pois em frequências elevadas a carga
pode drenar correntes elevadas. Para exemplificar, um AO deve ser capaz de suprir 63mA para uma
˙ ).
carga capacitiva de 10000pF excitada por um sinal de 10V e 100kHz ( i Lmáx =C L⋅V Omáx
Circuitos de compensação podem ser criados para evitar instabilidade. Como margens de
fase menores do que 45o costumam gerar picos na resposta em frequência, sobrepassos ou
oscilações na resposta ao degrau costuma-se usar uma estratégia conservadora de compensação
considerando que a influência do polo pCL pode ser percebida uma década antes. Existem diversas
possibilidades de compensar este circuito e algumas são discutidas nos artigos Op Amps Driving
Capacitive Loads e Practical Techniques to Avoid Instability Due to Capacitive Loading da Analog
Device. No circuito mostrado na Figura 6.9 foi implementada uma compensação interna ao laço de
realimentação. Esta é uma das mais conhecidas técnicas e mais eficientes quando a capacitância da
carga é conhecida. O resistor R3 desacopla a carga capacitiva e cria um polo e um zero que são
anulado por um zero e um polo na malha de realimentação com C1.
Se Ro ≪ R1 , Ro ≪ R2 e Ro ≪ R3 a compensação pode ser feita com
R3=
Ro⋅R 1
R o + R3
⋅C .
e C 1=
R2
R2
Figura 6.9: Compensador para cargas capacitivas.
Instrumentação e Técnicas de Medida – UFRJ, 2013/1
52