TRIÂNGULO RETÂNGULO

RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO
TRIÂNGULO RETÂNGULO
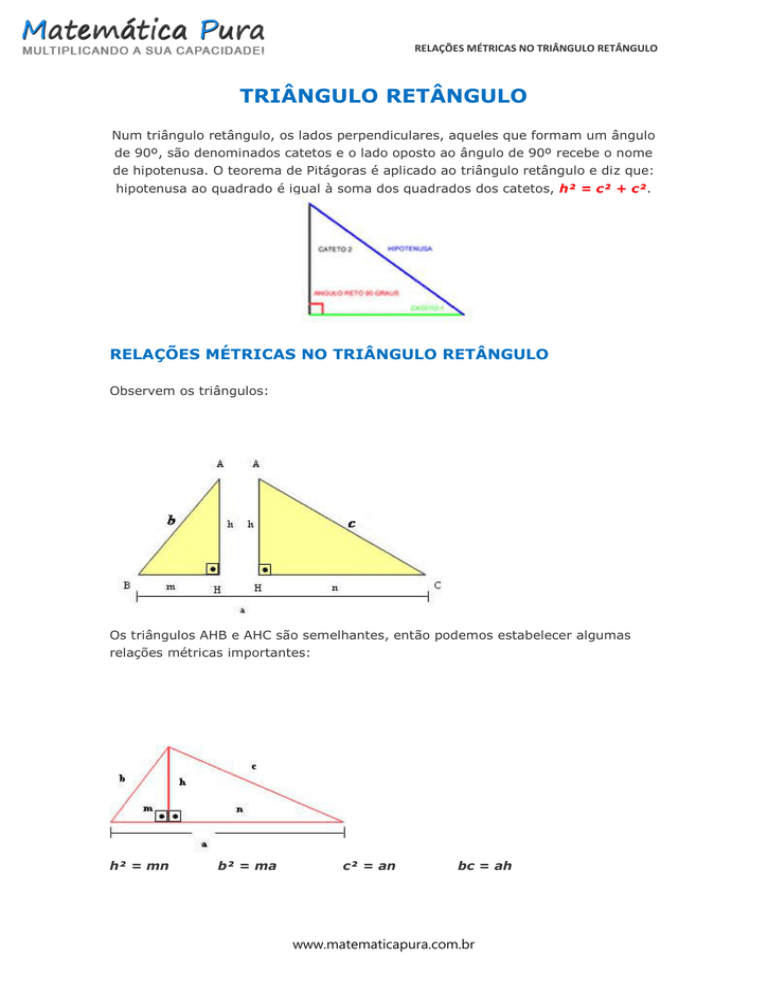
Num triângulo retângulo, os lados perpendiculares, aqueles que formam um ângulo
de 90º, são denominados catetos e o lado oposto ao ângulo de 90º recebe o nome
de hipotenusa. O teorema de Pitágoras é aplicado ao triângulo retângulo e diz que:
hipotenusa ao quadrado é igual à soma dos quadrados dos catetos, h² = c² + c².
RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO
Observem os triângulos:
Os triângulos AHB e AHC são semelhantes, então podemos estabelecer algumas
relações métricas importantes:
h² = mn
b² = ma
c² = an
bc = ah
www.matematicapura.com.br
RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO
APLICAÇÕES DO TEOREMA DE PITÁGORAS
DIAGONAL DO QUADRADO
Dado o quadrado de lado l, a diagonal D do quadrado será a hipotenusa de um
triângulo retângulo com catetos l, com base nessa definição usaremos o teorema
de Pitágoras para uma expressão que calcula a diagonal do quadrado em função da
medida do lado.
DIAGONAL DO BLOCO RETANGULAR (PARALELEPÍPEDO)
Observe o bloco de arestas a, b e c, iremos calcular a diagonal (d), mas usaremos a
diagonal x da base em nossos cálculos. Veja:
x² = a² + b²
d² = x² + c²
substituindo, temos:
www.matematicapura.com.br
RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO
ALTURA DE UM TRIÂNGULO EQUILÁTERO
O triângulo PQR é equilátero, vamos calcular sua altura com base na medida l dos
lados. Ao determinarmos a altura (h) do triângulo PQR, podemos observar um
triângulo retângulo PHQ catetos: h e l/2 e hipotenusa h. Aplicando o teorema de
Pitágoras temos:
www.matematicapura.com.br
RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO
DIAGONAL DO CUBO (CASO PARTICULAR DO PARALELEPÍPEDO)
Considere o cubo um caso particular de um bloco retangular, então:
a=b=c=l
TRIANGULO RETÂNGULO (seno, cosseno e tangente)
Em um triângulo retângulo, seno, cosseno e tangente são definidos por:
PS triângulo retângulo em C:
Seno (em inglês e na maioria das linguagens de programação e calculadoras, sin):
Cosseno (em linguagens de programação e calculadoras, cos):
Tangente (na maioria das linguagens de programação e calculadoras, tan, mas
também é possível encontrar tang e tg):
Observando-se, na figura, que os ângulos A e B somam um ângulo reto.
(
, em radianos), chega-se a:
www.matematicapura.com.br
RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO
Elementos de um triângulo retângulo
No triângulo retângulo ABC da figura acima, temos:
www.matematicapura.com.br
RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO
DEMONSTRANDO AS RELAÇÕES MÉTRICAS NUM TRIÂNGULO
RETÂNGULO
VEJAMOS:
www.matematicapura.com.br
RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO
RELAÇÕES DAS SEMELHANÇAS DOS TRIÂNGULOS:
1) Através da relação de Euclides, podemos dizer que o quadrado da medida de um
cateto, é o mesmo que o produto da medida da hipotenusa através da medida da
projeção ortogonal deste mesmo cateto sobre a hipotenusa.
www.matematicapura.com.br
RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO
2) Através do Teorema de Pitágoras, podemos dizer que o quadrado da medida
da hipotenusa, é o mesmo que a soma dos quadrados das medidas dos catetos.
Logo, temos:
www.matematicapura.com.br
RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO
3) Há uma igualdade entre o quadrado da medida da altura relativa e o produto das
medidas das projeções dos catetos sobre a hipotenusa.
Logo, temos:
4) O produto da medida da hipotenusa pela medida da altura relativa à hipotenusa
será igual ao produto das medidas dos catetos.
Logo, temos:
www.matematicapura.com.br
RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO
RESUMO DAS RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO
No triângulo retângulo ABC da figura, onde BC = a, AC = b; AB = c; AH = h; BH =
m e CH = n, valem as seguintes relações, vejamos:
www.matematicapura.com.br
RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO
RAZÕES TRIGONOMÉTRICAS (demonstrações)
Considere um triângulo retângulo ABC. Podemos definir:
- Seno do ângulo agudo: razão entre o cateto oposto ao ângulo e a hipotenusa
do triângulo.
senÊ = e/a
senÔ = o/a
www.matematicapura.com.br
RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO
- Cosseno do ângulo agudo: razão entre o cateto adjacente ao ângulo e a
hipotenusa do triângulo.
cosÊ = o/a
cosÔ = e/a
- Tangente do ângulo agudo: razão entre o cateto oposto ao ângulo e o cateto
adjacente.
tgÊ = e/o
tgÔ = o/e
Observe: senÊ = cosÔ, senÔ = cosÊ e tgÊ = 1/tgÔ, sempre Ê + Ô = 90º
Exemplo:
senÔ = 3/5 = 0,6
cosÔ = 4/5 = 0,8
tgÔ = 3/4 = 0,75
senÊ = 4/5 = 0,8
cosÊ = 3/5 = 0,6
tgÊ = 4/3 = 1,333....
ÂNGULOS NOTÁVEIS
Pode-se determinar seno, cosseno e tangente de alguns ângulos. Esses
ângulos chamados de notáveis são: 30°, 45° e 60°. A partir das definições de
seno, cosseno e tangente, vamos determinar esses valores para os ângulos
notáveis. Considere um triângulo equilátero de lado l Traçando a altura AM,
obtemos o triângulo retângulo AMC de ângulos agudos iguais a 30° e 60°.
Aplicando as razões trigonométricas ao triângulo AMC temos:
www.matematicapura.com.br
RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO
Para obter as razões trigonométricas do ângulo de 45°, considere um quadrado
de lado l. A diagonal divide o quadrado em dois triângulos retângulos isósceles.
No triângulo ABD, temos:
www.matematicapura.com.br
RELAÇÕES MÉTRICAS NO TRIÂNGULO RETÂNGULO
Observação: sen45° = cos45°
TABELA DOS ÂNGULOS NOTÁVEIS:
www.matematicapura.com.br