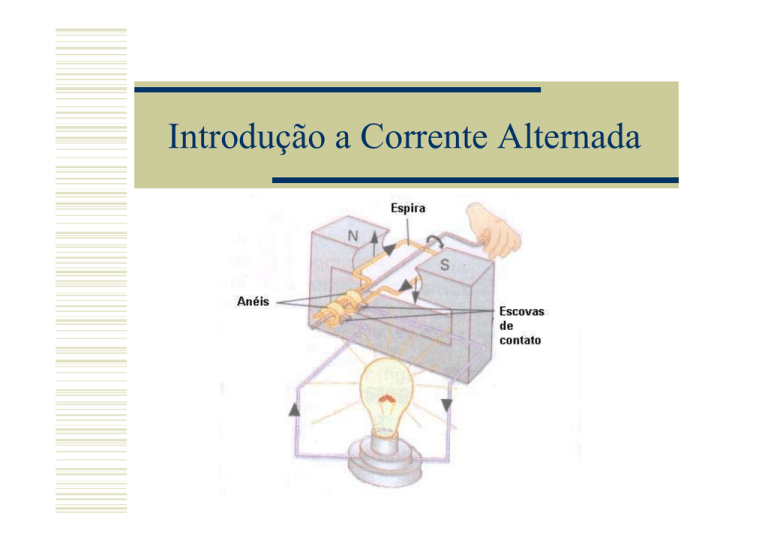
Introdução a Corrente Alternada
Tensão Continua
Uma tensão é chamada de continua ou
constante quando o seu valor não se altera
com o tempo.
Exemplo de geradores que geram tensão
continua são as pilhas e as baterias.
A Figura a seguir mostra o aspecto físico,
símbolo e curva da tensão em função do
tempo deste tipo de gerador.
Exemplo de Fonte de Tensão
Contínua
Tensão Alternada
É uma tensão cujo valor e polaridade se
modificam ao longo do tempo. Conforme o
comportamento da tensão, temos os
diferentes tipos de tensão:
Senoidal, quadrada, triangular, pulsante,
etc.
De todas essas, analisaremos a partir de
agora a senoidal, porque é a tensão fornecida
nas fontes geradoras e que alimenta as
industrias e residências.
Tensão Alternada
Seja o circuito da próxima Figura, no qual
temos duas baterias e uma chave que ora
conecta a bateria B1 ao resistor, ora conecta
a bateria B2 ao resistor.
Vamos supor que cada
bateria fica conectada ao
resistor durante 1s.
Como seria o gráfico da
tensão em função do tempo nos
terminais da bateria ?
Exemplo de Geração Alternada
•
O valor negativo significa que a polaridade da tensão mudou. Desta forma
obtemos uma forma de onda quadrada. Além desta, usualmente temos aplicações
em eletricidade as formas triangular e principalmente a senoidal.
•
O tempo que leva para repetir uma mesma situação é 2s, sendo chamado de
período (T). O valor máximo da tensão é 12V ( sendo chamado de valor de pico
ou valor máximo VM). A seguir analisaremos mais em detalhes a senoidal.
Tensão Senoidal
É uma tensão que varia com o tempo de
acordo com uma função senoidal
A expressão matemática é dada pela função:
v(t ) = VM .sen(ω .t + θ )
Onde VM é o valor de pico (valor máximo que a tensão
pode ter) , em (rad/s) é a freqüência angular e (rd ou
graus) é o angulo de fase inicial.
Representação Gráfica
VPP (em V) é chamado de tensão de pico a
pico, T (em s) é o período da função.
Representação gráfica de uma tensão
senoidal em função do angulo
A rotação da bobina ao longo de 360º geométricos( 1
rotação ) gera sempre 1 ciclo ( 360º) de Tensão (
Gerador de 2 pólos).
Corrente Alternada
Quando uma tensão senoidal é ligada aos terminais
de uma resistência de carga, a corrente também é
uma onda senoidal.
Exemplo
Exemplo 1:
Uma tensão senoidal ca é
aplicada a uma resistência
de carga de 10 >. Mostre a
onda senoidal resultante
para a corrente alternada.
O Valor instantâneo da
corrente
é
i=v/R. Num
circuito
apenas
com
resistência, a forma de onda
da corrente segue
a
polaridade da forma de onda
da tensão.
Como a corrente é definida
pela expressão:
i = I M .senθ
O valor máximo da corrente é
IM =
VM 10
= = 1A
R 10
Graficamente, é representado por:
Freqüência e Período
O número de ciclos por minuto é chamado de Freqüência.
É representada pela letra f e unidade em hertz [Hz].
O intervalo de tempo para que um ciclo se complete é chamado de período.
É representado pelo símbolo T e expresso em segundos [s].
A freqüência é o recíproco do período, ou seja:
f =
1
T
e
T=
1
f
Quanto maior a freqüência,
menor o período.
Relação entre graus
elétricos e tempo
O ângulo de 360º representa o tempo para um ciclo,
ou período T.
Portanto, temos a seguinte representação gráfica.
Exemplo
Exemplo 2
Uma corrente ca varia ao longo de um ciclo completo em 1/100s. Qual
o período e a freqüência? Se a corrente tiver um valor máximo de 5A,
mostre a forma de onda para a corrente em graus e em segundos.
T=
1
s
100
ou
10ms
Graficamente
ou 10ms
f =
1
1
=
= 100 Hz
T 1/100
Relações de Fase
O ângulo de fase entre duas formas de onda de mesma freqüência é a
diferença angular num dado instante.
Na figura abaixo, o ângulo de fase entre as ondas B e A é de 90º
Enquanto a onda A começa com seu valor máximo e cai para zero em
90º.
A onda B atinge o seu valor máximo 90º na frente de A.
Este ângulo de fase de 90º entre as ondas B e A é mantido durante o
ciclo completo e todos os ciclos sucessivos.
Fasores
Forma alternativa para representação de correntes e tensões
alternadas (senoidais).
Um fasor é uma entidade com módulo e sentido.
O comprimento do fasor representa o módulo da
tensão/corrente alternada.
O ângulo em relação ao eixo horizontal indica ao ângulo de fase.
Representação Fasorial
Tomando com exemplo a figura abaixo, o fasor VA representa a
onda de tensão A com ângulo de fase de 0º.
O fasor VB é vertical para mostrar o ângulo de fase de 90º com
relação ao fasor VA, que serve de referência.
Representação Fasorial
Quando duas ondas estão em fase, o ângulo de fase é
zero. As amplitudes se somam.
Quando as ondas estão exatamente fora de fase, o
ângulo de fase é de 180º. Suas amplitudes são
opostas.
Exemplo
Exemplo 3
Qual o ângulo de fase entre as ondas A e B? Faça o diagrama de fasores primeiro
com a onda A como referência e depois como a onda B como referência.
Ângulo de fase é a distância angular entre pontos
correspondentes nas ondas A e B.
Os pontos correspondentes mais convenientes sâo os pontos
de máximo, dos mínimos e dos zeros de cada onda.
No cruzamento dos zeros no eixo horizontal, =30º.
A como referência
B como referência
Valores Características de
Tensão e de Corrente
Valor de pico é o valor máximo VMax ou IMax.
Valor de pico a pico é igual ao dobro do valor de pico, quando os picos positivo e
negativo são simétricos.
Valor médio, corresponde à média aritmética de todos os valores numa onda
senoidal, considerando um meio ciclo.
Valor Medio = 0,637 x valor de pico
VM = 0,6237.VMax
I M = 0,637.I Max
O valor rms de uma onda senoidal corresponde à mesma quantidade de tensão
ou corrente contínua capaz de produzir a mesma potência dissipada.
O valor eficaz ou rms ou valor médio quadrático corresponde a 0,707 vezes o
valor de pico.
Valor rms = 0,707 x valor de pico
VM = 0,707.VMax
I M = 0,707.I Max
Valores Características de
Tensão e de Corrente
Resistência em Circuitos CA
Em circuitos ca somente com resistência.
Tensão e Corrente estão em fase.
Esta relação entre V e I em fase, significa que este circuito ca
pode ser analisado pelos métodos usados para o circuito cc.
Seja o circuito, abaixo, em série.
I=
V 110
=
= 11A
R 10
P = I 2 .R = 112.10 = 1210W
Exercício
Exercício 1
Calcule o ângulo
de fase para as
seguintes ondas
ca e desenhe os
respectivos
diagramas de
fasores
45o
45o
Exercício
Indutância, Reatância e
Circuitos Indutivos
A capacidade de um condutor possui de induzir tensão em si
mesmo quando a corrente varia é chamada de auto-indutância
ou simplesmente indutância.
vl
L=
∆i
∆t
Onde:
L= indutância, [H]
v= tensão induzida através da bobina, [V]
'i/'t= taxa de variação da corrente, [A/s]
Indutância Mútua
Quando a corrente num condutor ou numa bobina varia, este
fluxo pode interceptar qualquer outro condutor ou bobina nas
vizinhanças, induzindo tensões em ambos.
Características das Bobinas
A indutância de uma bobina depende de como ela é enrolada, material
do núcleo em torno do qual é enrolada, e do número de espiras que
formam o enrolamento.
A indutância L aumenta com o número de espiras N em torno do núcleo. A
indutância aumenta com o quadrado do número de espiras.
A indutância aumenta com a permeabilidade relativa r do material de que
é feito o núcleo.
À medida que a área A abrangida em cada espira aumenta. A indutância
aumenta com o quadrado do diâmetro.
A indutância diminui à medida que o comprimento da bobina aumenta.
2
N .A
−6
L = µr .
1, 26 x10 ) ,[ H ]
(
l
Reatância Indutiva
A reatância indutiva XL é a oposição à corrente ca
devida à indutância do circuito.
A unidade da reatância indutiva é o ohm.
A fórmula para a reatância indutiva é
X L = 2.π . f .L
Onde
XL= reatância indutiva,[>]
f = freqüência angular,[Hz]
L = indutância, [Hz]
Indutores em série
Se os indutores forem dispostos afastados um do outro de modo
que não interajam eletromagneticamente entre si.
Podem ser associados como resistores.
LT = L1 + L2 + L3 + ........ + Ln
Se duas bobinas ligadas em série
forem colocadas próximas de modo
que linhas de campo magnético se
interliguem.
A indutância total será:
LT = L1 + L2 ± 2.LM
Indutores em paralelo
Afastados, de modo que a indutância mútua seja
desprezível, tem-se que:
1
1 1
1
1
= + + + ........ +
LT L1 L2 L3
Ln
No caso de apenas duas bobinas em paralelo, tem-se
que:
L1.L2
LT =
L1 + L2
Circuitos Indutivos
Seja uma tensão ca, v, aplicada a um circuito que tenha
somente indutância.
A corrente iL, que passa pela indutância estará atrasada da
tensão vL, de 90º.
Circuito RL em série
Quando uma bobina têm uma resistência em série, a corrente I é
limitada tanto por XL quanto por R.
A corrente I , através de XL, está defasada da tensão VL de 90º.
VR = I .R
e
VL = I . X L
Exemplo
Exemplo 4
Um circuito ca com RL em série tem uma corrente de 1A de pico, com R=50 > e XL=50
>.
Calcule VR, VL, VT e . Faça o diagrama de fasores de VT e I. Faça também o diagrama
de tempo i, vR, vL e vT.
Impedância RL série
A resultante da adição dos fasores R e XL é chamada de
impedância. É representada pelo símbolo Z.
A impedância é a reação total ao fluxo da corrente em ohms [>].
VT2 = VR2 + VL2
( I .Z )
2
= ( I .R ) + ( I . X L )
2
2
Z 2 = R 2 + X L2
Z = R 2 + X L2
XL
XL
tgθ =
→ θ = arctg
R
R
Circuito RL paralelo
Para circuitos paralelo contendo R e XL , uma mesma tensão VT
está aplicada a eles.
Portanto esta tensão será usada como referência.
Exemplo
Impedância RL paralelo
Cálculo a partir da tensão como referência.
Exemplo: Qual a impedância de ZT de um R de 200 > em paralelo
com XL de 400 >? Suponha que a tensão VT seja de 400 V.
IR =
VT 400
=
= 2A
R 200
IL =
VT 400
=
= 1A
X L 400
IT = I R2 + I L2 = 4 + 1 = 5 = 2, 24 A
VT
400
ZT =
=
= 178, 6Ω
IT 2, 24
Potência em circuitos RL
Num circuito ca com reatância indutiva, a corrente está
atrasada em relação a tensão aplicada.
Existe neste caso 3 tipos de potência.
Pot. real P = V ( I .cos θ ) = VI cos θ
Pot. reativa Q = V ( I .senθ ) = VIsenθ
Pot. aparente S = VI
Tensão e corrente expressos em valor rms.
Exemplo
Exemplo 6
O circuito ca tem 2A através de um R de 173 Ω em série com um XL de 100
Ω. Calcule o fator de potência, a tensão aplicada V, a potência real P, a
potência reativa Q e a potência aparente S.
X
100
θ = arctg L = arctg
= arctg 0,578 = 30o
R
173
FP = cos θ = cos 30o = 0,866
R
173
=
= 200Ω
Z=
cos θ cos 30º
V = I .Z = 2(200) = 400V
P = I 2 R = 22.(173) = 692W
ou
P = V .I .cosθ = 400.(2).(cos 30º ) = 692W
Q = V .I .senθ = 400.(2).( sen30º ) = 400VAr
S = V .I = 400.(2) = 600VA
Capacitância, Reatância
Capacitiva e Circuitos Capacitivos
Um capacitor é um dispositivo elétrico
formado por duas placas condutoras de metal
separadas por um material isolante chamado
dielétrico.
Capacitância
O capacitor armazena carga elétrica no dielétrico.
Capacitância
Capacitância
Capacidade de armazenamento de carga elétrica.
Quantidade de carga que pode ser armazenada num
capacitor dividida pela tensão aplicada às placas.
Q
C=
V
Onde
C=capacitância,F
Q= quantidade de carga,C
V=tensão,V
Capacitores em série e em
paralelo
Associação série.
1
1
1
1
1
= +
+
+ ...................
CT C1 C2 C3
Cn
Associação paralelo.
CT = C1 + C2 + C3 + ...................Cn
Reatância Capacitiva
A reatância capacitiva XC é a oposição
ao fluxo de corrente.
Unidade: [ohm] ou [>].
1
1
0,159
XC =
=
=
2.π . f .C 6, 28. f .C
f .C
Onde
XC = reatância capacitiva, >
f = freqüência, Hz
C = capacitância, F
Circuitos Capacitivos
Somente Capacitância.
Circuitos RC Série
A associação da resistência com a reatância
capacitiva é chamada de impedância.
V = V +V
2
T
2
R
2
C
VC
VC
→ θ = arctg −
tgθ = −
VR
VR
Exemplo
Exemplo 7. Um circuito ca RC em série tem uma
corrente de pico de 1 A com R=50 > e XC=120 >.
Calcule VR, VC, VT e . Faça o diagrama de fasores