Trabalho 2 - Grupo 5 Arquivo

Trab. escr.: 4,0/5,0
Matlab: 2,0/3,0
Psim: 2,0/2,0
NOTA: 8,0
Trabalho de Medidas e Circuitos Elétricos
apresentação do
trabalho?
Professor: Azauri Albano de Oliveira Junior .
Trabalho 2.
Data de entrega: 26/09/2016
Grupo 5 (André Luiz de Souza, Edisa Almengor, Gabriel Chicória, Henrique Megid, Luíz
Gabriel Rolim, Rafael Baquero).
Algoritmo:
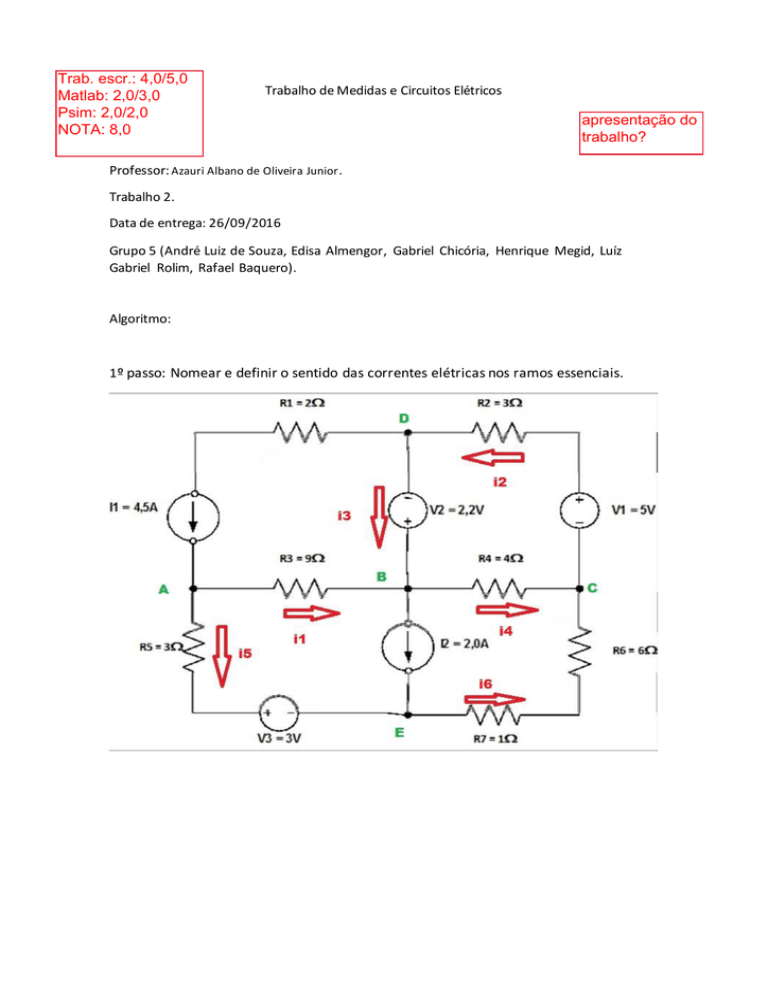
1º passo: Nomear e definir o sentido das correntes elétricas nos ramos essenciais.
2º passo: Atribuir o sentido de queda das tensões nos resistores e nas fontes de
corrente independente.
3º passo: Montar as equações das tensões em função das corrente para cada dipolo
isoladamente, seguindo V = R.i.
V1 = 9 v
V2 = 3 . i2
V3 = 9 . i1
V4 = 4 . i4
V5 = 3 . i5
V6 = 6 . i6
V7 = 1 . i6
4º passo: Aplicar a Lei de Kirchhoff para as correntes (LKC) nos nós essenciais (A, B, C,
D, E), montando as equações seguindo a somatória das correntes de entrada e saída
dos nós, atribuindo o sentido de entrada como positivo e o de saída como negativo.
Foram obtidas cinco equações.
A: 4.5 = i1 + i5
B: i3 + i1 = i4 + 2
C: i4 + i6 = i2
D: i2 = i3 + 4.5
E: 2 + i5 = i6
5º passo: Descartar uma das equações do LKC em virtude da dependência linear em
relação as demais.
Descartou-se a “C”.
6º passo: Aplicar a Lei de Kirchhoff para as tensões (LKT) nas malhas (alfa, beta, gama,
delta), atribuindo um sentido para a leitura das tensões dentro de cada malha e
montando as equações segundo a somatória das tensões.
Alfa: -2.2 + 4 . i4 – 5 + 3 . i2 = 0
Beta: -2.2 – 9 . i1 – U1 – 9 = 0
Gama: U2 – 3 – 3 . i5 + 9 . i1 = 0
Delta: U2 + i6 + 6 . i6 – 4 . i4 = 0
7º passo: Isolar as correntes em um membro das equações e as tensões em outro.
A: i1 + i5 = 4.5
B: i1 + i3 – i4 = 2
D: I2 – i3 = 4.5
E: i6 – i5 = 2
Alfa: 4 . i4 + 3 . i2 = 7.2
Beta: -9 . i1 – U1 = 11.2
Gama: 9 . i2 – 3 . i5 + U2 = 3
Delta: 7 . i6 – 4 . i4 + U2 = 0
8º passo: Converter o sistema linear do conjunto das equações obtidas para o formato
matricial, respeitando a equação V = R.i (primeira lei de Ohm).
=
9º passo: Colocando as Matrizes V e R e i no programa Matlab, determinar a Matriz i
através da fórmula I = V x 𝑅 −1 .
=
10º passo: Utilizando as correntes obtidas, substituir seus valores na fórmula V = R.i
em cada dipolo do circuito, para poder obter as suas respectivas tensões.
V1 = 9 v
V2 = 8.5158 v
V3 = 29.9916 v
V4 = -1.316 v
V5 = 3.5028 v
V6 = 19.0056 v
V7 = 3.1676 v
11º passo: Com as tensões e as correntes de cada dipolo do circuito determinadas, foi
feita a seguinte tabela, que apresenta o balanço geral de energia por meio das
potências (𝑃 = ± 𝑉 . 𝐼).
Tabela:
Dipolo
F.T.I 1
F.T.I 2
F.T.I 3
F.C.I 1
F.C.I 2
Resistor 1
Resistor 2
Resistor 3
Resistor 4
Resistor 5
Resistor 6
Resistor 7
Corrente (A)
2,84
-1,66
1.16
4,5
2
4,5
2,84
3,33
-0,33
1,17
3,17
3,17
Tensão (V)
5
2,2
3
-41,19
-23,99
9
8,52
29,99
-1,32
3,50
19,01
3,17
Potência (W)
-14,19
3,66
3.50
-185,35
-47,98
40,5
24,20
99,87
0,43
4,09
60,26
10,05
Comportamento
Gerador
Receptor
Receptor
Gerador
Gerador
Receptor
Receptor
Receptor
Receptor
Receptor
Receptor
Receptor
Legenda: Fonte de Tensão Independente (F.T.I); Fonte de Corrente Independente
(F.C.I).
Energia Total Gerada: - 247,52 W
Energia Total Consumida: + 246,56 W
Balanço Geral: - 0.96 W
Diferença essa causada pelas aproximações nos cálculos.
Fim do algoritmo.
psim:
funcionou.
matlab:
funcionou, a
rotina está
escrita de forma
clara, mas não
aproveitou a
rotina para
determinar as
potências e o
balanço de
potências.