16/03/13 PROFESSOR: MALTEZ

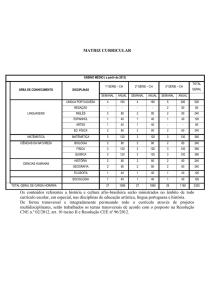
RESOLUÇÃO DA AVALIAÇÃO DE MATEMÁTICA
2o ANO DO ENSINO MÉDIO
DATA: 16/03/13
PROFESSOR: MALTEZ
01. Seja (an) a sequência dada pelo termo geral an = (–1)n .
a2 = (–1)2 .
2+2 4
=
2 +1 3
a5 = (–1)5 .
7
5+2
7
= –1 . = –
6
5 +1
6
a2 + a5 =
n+2
. A soma a2 + a5 é igual a:
n +1
4 7 8−7 1
– =
=
3 6
6
6
02. Três números estão em PA. O produto deles é 66 e a soma é 18. O maior dos números é:
Os números em PA são x – r, x, x + r
x – r + x + x + r = 18 ⇒ x = 6
(x – r) . x . (x + r) = 66 ⇒ (6 – r) . 6 . (6 + r) = 66
36 – r2 = 11
r2 = 25 ⇒ r = ±5
Os números são 1, 6 e 11 onde o maior é 11.
03. Em uma PA crescente, a2 + a6 = 20 e a4 + a9 = 35.
Então o décimo primeiro termo dessa PA é:
a2 + a6 = 20 ⇒2a1 + 6r = 20
a4 + a9 = 35 ⇒2a1 + 11r = 35
Subtraindo membro a membro: –5r = –15 ⇒ r = 3
Substituindo na 1a: 2a1 + 18 = 20 a1 = 1
a11 = a1 + 10r = 1 + 10 . 3 = 31
04. Sabendo que as parcelas do 1o membro da igualdade 2 + 7 + ... + 2x = 198 formam uma PA, o valor
de x é:
an = a1 + (n – 1)r ⇒ 2x = 2 + (n – 1) . 5 ⇒
n=
2x + 3
5
Aplicando a fórmula da soma:
 2x + 3 

(2 + 2x ) . 
5 
(a1 + an) . n

198 =
⇒ 198 =
2
2
'
x = 21
⇒ 2x2 + 5x – 987 = 0
x” = –
47
2
Como a PA é crescente e n > 0
x = 21
05. Um teatro possui 12 poltronas na primeira fila, 14 na segunda, 16 na terceira e assim por diante,
sempre na mesma sequência. Para o teatro ter 620 poltronas, o número de fileiras necessárias são:
12 + 14 + 16 + ... + an = 620
(a1 + an )n
= 620. Como
2
an = 12 + (n – 1) . 2 ⇒ an = 10 + 2n
Substituindo:
(12 + 10 + 2n)n
= 620 ⇒ n2 + 11n – 620 = 0
2
que produz as raízes n = 20 e n = – 31 (que não satisfaz). Portanto, a resposta é 20 fileiras.
06. Os números x + 1, x + 4 e x + 10, formam, nessa ordem, uma PG. Então o termo do meio é:
(x + 1, x + 4, x + 10) PG
(x + 4)2 = (x + 1) (x + 10)
x2 + 8x + 16 = x2 + 11x + 10 ⇒ x = 2
Os números formam a PG:
(3, 6, 12) o que significa que o termo do meio é 6.
07. Numa PG, a soma do 3o e do 5o termo é igual a 360, e a soma do 4o e do 6o termo é igual a 1080.
Então o oitavo termo dessa PG é:
a3 + a5 = 360
⇒
a1 . q2 + a1 . q4 = 360
a4 + a6 = 1080
⇒
a1 . q3 + a1 . q5 = 1080
a1 . q2 (1 + q2) = 360
Fatorando:
(:) e
a1 . q3 (1 + q2) = 1080
dividindo a 2a pela 1a: q = 3
Subst. na 1a: a1 . 32 (1 + 32) = 360
a1 . 90 = 360 ⇒ a1 = 4
a8 = a1 . q7 = 4 . 37 = 4 . 2187 = 8748
08. A soma dos seis termos iniciais de uma PG é 1456. Sabendo que a razão dessa PG é 3, o primeiro
termo é igual a:
S6 =
a1(q6 − 1)
q −1
(
)
1456 =
a1 36 − 1
3 −1
1456 =
a1 . 728
2
⇒ 1456 = 364a
1
a1 = 4
09. Um sitiante estava perdendo sua plantação de algodão em decorrência da ação de uma praga. Ao
consultar um agrônomo da Casa da Lavoura, foi orientado para que pulverizasse, uma vez ao dia,
um determinado agrotóxico da seguinte maneira: 1o dia: 2 litros, 2o dia: 4 litros, 3o dia: 8 litros e
assim sucessivamente. Sabendo que o total de agrotóxico pulverizado foi de 126 litros, quantos
dias de duração teve esse tratamento?
2 + 4 + 8 + ..........an = 126
n
2(2 − 1)
a1(q n − 1)
= 126 ⇒
= 126
q −1
2 −1
2 . (2n – 1) = 126 ⇒ 2n – 1 = 63
2n = 64 ⇒ n = 6
1
1
+ 2 + .....
10 10
, na qual o numerador e o denominador são os limites das
10. O valor da expressão
1 1
1+ +
+ ....
4 16
somas de duas PG’s infinitas, é:
1+
O limite da soma é Sn =
a1
1− q
para |q| < 1.
1+
1+
1
1
+ 2 + ... =
10 10
1 1
+
+ ... =
4 16
1
1−
1
1−
1
4
1
10
=
=
1
10
=
9
9
10
1 4
=
3 3
4
10
5
10
3 5
x =
A expressão fica: 9 =
4
9 42 6
3
3
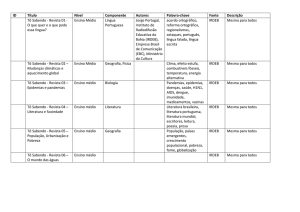
QUESTÕES DISCURSIVAS
01. Quantos números inteiros compreendidos entre 1 e 1500 são divisíveis por 3 e por 7 ao mesmo
tempo?
Divisíveis ao mesmo tempo por 3 e por 7 significa que são os divisíveis por 21.
Assim entre 1 e 1500:
(21, 42, 63, ......., 1491)
formam uma PA de razão 21.
an = a1 + (n – 1) r
1491 = 21 + (n – 1) . 21
1470 = (n – 1) . 21
70 = n – 1 ⇒ n = 71
02. Escrevendo-se quatro números entre 480 e 15, obtém-se uma sequência de uma PG. Determine a
razão dessa PG.
Se a sequência é uma PG:
(480,...., 15)
o número total de termos da PG é n = 6
an = a1 . q n – 1
15 = 480 . q5
1
q = 2
3
5
⇒
5
 1
1
q =   ⇒ q =
2
2
5
03. Numa PG crescente, são dados a2 = 6 e a4 = 54.
Calcule a soma dos cinco primeiros termos dessa PG.
Sabe-se que a4 = a2 . q2
54 = 6 . q2
q2 = 9
q = 3 (pois a PG é crescente). Como a2 = a1 . q,
a1 . q = 6 ⇒ a1 . 3 = 6 ⇒
a1 = 2
a1 . (q5 − 1) 2(35 − 1) 2 . 242
S5 =
=
=
= 242
q −1
3 −1
2
04. Resolva a equação 5x +
10 x 20 x
+
+ .... = 20, na qual o primeiro membro é o limite da soma de uma
3
9
PG infinita.
O limite da soma é Sn =
5x
5x
⇒ 20 =
1
2
1−
3
3
20 = 15x
20 =
x=
20
4
⇒ x=
15
3
a1
1− q
05. São dados quatro números x, y, 6, 4, nessa ordem.
Sabendo que os três primeiros estão em PA e os três últimos estão em PG determine x e y.
(x, y, 6) ⇒ PA ⇒ y =
x+6
2
(y, 6, 4) ⇒ PG ⇒ 62 = 4y ⇒ y = 9
y=
x+6
x+6
⇒9=
2
2
18 = x + 6
x = 12