Problemas Resolvidos de Física

PROBLEMAS RESOLVIDOS DE FÍSICA
Prof. Anderson Coser Gaudio
Departamento de Física – Centro de Ciências Exatas – Universidade Federal do Espírito Santo
http://www.cce.ufes.br/anderson
[email protected]
Última atualização: 28/11/2006 15:00 H
23 - Campo Magnético
Fundamentos de Física 2
Halliday, Resnick, Walker
4ª Edição, LTC, 1996
Cap. 30 - O Campo
Magnético
Física 2
Resnick, Halliday, Krane
4ª Edição, LTC, 1996
Cap. 34 - O Campo
Magnético
Física 2
Resnick, Halliday, Krane
5ª Edição, LTC, 2003
Cap. 32 - O Campo
Magnético
Prof. Anderson (Itacaré, BA - Fev/2006)
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
HALLIDAY, RESNICK, WALKER, FÍSICA, 4.ED., LTC, RIO DE JANEIRO, 1996.
FUNDAMENTOS DE FÍSICA 3
CAPÍTULO 30 - O CAMPO MAGNÉTICO
EXERCÍCIOS E PROBLEMAS
01
11
21
31
41
51
61
71
81
91
02
12
22
32
42
52
62
72
82
92
03
13
23
33
43
53
63
73
83
93
04
14
24
34
44
54
64
74
84
94
05
15
25
35
45
55
65
75
85
95
06
16
26
36
46
56
66
76
86
96
07
17
27
37
47
57
67
77
87
97
08
18
28
38
48
58
68
78
88
98
09
19
29
39
49
59
69
79
89
99
10
20
30
40
50
60
70
80
90
100
[Início documento]
[Início seção]
[Início documento]
________________________________________________________________________________________________________
a
Cap. 30 – O Campo Magnético
Halliday, Resnick, Walker - Física 3 - 4 Ed. - LTC - 1996.
2
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
RESNICK, HALLIDAY, KRANE, FÍSICA, 4.ED., LTC, RIO DE JANEIRO, 1996.
FÍSICA 3
CAPÍTULO 34 - O CAMPO MAGNÉTICO
PROBLEMAS
01
11
21
31
41
51
61
02
12
22
32
42
52
62
03
13
23
33
43
53
63
04
14
24
34
44
54
64
05
15
25
35
45
55
06
16
26
36
46
56
07
17
27
37
47
57
08
18
28
38
48
58
09
19
29
39
49
59
10
20
30
40
50
60
[Início documento]
07. Um elétron tem velocidade v = 40i + 35j km/s, num campo magnético uniforme. Sabendo-se
que Bx = 0, calcule o campo magnético que exerce sobre o elétron uma força F = −4,2i + 4,8j
fN.
(Pág. 149)
B
Solução.
A força magnética é dada pela expressão:
F = qv × B
Podemos desenvolver a expressão acima, substituindo-se o valor dado de v e uma expressão
genérica para B (lembre-se que Bx = 0):
B
F = q ( vx i + v y j) × ( By j + Bz k )
Operando-se o produto vetorial, teremos:
F = q ( v y Bz i − vx Bz j + vx By k )
Como a expressão da força dada no enunciado não possui componente k, temos:
F = q ( v y Bz i − vx Bz j)
Substituindo-se por valores numéricos:
F = ( −1, 60 ×10−19 C ) ⎡⎣( 35 ×103 m/s ) Bz i − ( 40 ×103 m/s ) Bz j⎤⎦
F = ( −5, 60 ×10−15 C.m/s ) Bz i + ( 6, 40 ×10 −15 C.m/s ) Bz j
Comparando-se com o valor dado de F:
F = ( −4, 2 ×10 −15 N ) i + ( 4,8 ×10 −15 N ) j
Conclui-se que:
( −4, 2 ×10
−15
N ) = ( −5, 60 ×10 −15 C.m/s ) Bz
Bz = 0, 75 T
________________________________________________________________________________________________________
a
Cap. 34 – O Campo Magnético
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
3
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
Como B só possui componente em z, temos:
B = ( 0, 75 T ) k
[Início seção]
[Início documento]
10. Um elétron tem uma velocidade inicial de 12,0j + 15,0k km/s e uma aceleração constante de
(2,00 × 1012 m/s2)i no interior de uma região onde existem um campo elétrico e um campo
magnético uniformes. Determine o campo elétrico E, sabendo-se que B = 400i μT.
(Pág. 150)
Solução.
A força resultante F sobre o elétron é a soma da força elétrica FE com a força magnética FB.
F = FE + FB = mea
B
qE + qv × B = mea
E=
me
a − v×B
q
Substituindo-se por valores numéricos:
( 9,11×10 kg ) 2, 00 ×10 m/s i −
E=
(
)
( −1, 60 ×10 C )
− ⎡⎣(12, 0 ×10 m/s ) j + (15, 0 ×10 m/s ) k ⎤⎦ × ( 400 ×10
−31
12
2
−19
3
3
−6
T) i
E = − (11,3875" N/C ) i − ⎡⎣( 6, 00 N/C ) j − ( 4,80 N/C ) k ⎤⎦
E ≈ ( −11, 4i − 6, 00 j + 4,80k ) N/C
[Início seção]
[Início documento]
12. Um elétron com 1,22 keV está circulando num plano ortogonal a um campo magnético
uniforme. O raio da órbita é 24,7 cm. Calcule (a) a velocidade escalar do elétron, (b) o campo
magnético, (c) a freqüência de revolução e (d) o período.
(Pág. 150)
Solução.
[Início seção]
[Início documento]
15. Uma partícula alfa (q = +2e, m = 4,0 u) se move em uma trajetória circular com 4,5 cm de raio,
num campo magnético com B = 1,2 T. Calcule (a) sua velocidade escalar, (b) seu período de
revolução, (c) sua energia cinética em eV e (d) a diferença de potencial necessária para que a
partícula alcance essa energia.
(Pág. 150)
Solução.
(a) A força magnética FB que atua sobre a partícula assume a função da força centrípeta Fc do
movimento circular. Logo:
Fc = FB
B
________________________________________________________________________________________________________
a
Cap. 34 – O Campo Magnético
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
4
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
mv 2
= 2evB
r
−19
2erB 2 (1, 60 ×10 C ) ( 0, 045 m )(1, 20 T )
v=
=
= 2, 6024" ×106 m/s
−27
m
( 6, 64 ×10 kg )
v ≈ 2, 6 ×106 m/s
(b) O período de revolução da partícula vale:
T=
2π ( 0, 045 m )
2π r
=
= 1, 0864" ×10−7 s
6
v
"
2,
6024
m/s
×10
(
)
T ≈ 0,11 μ s
(c) A energia cinética da partícula vale:
2
1
1
K = mv 2 = ( 6, 64 ×10−27 kg )( 2, 6024" ×106 m/s ) = 2, 2484" ×10−14 J
2
2
eV
K = 2, 2484" ×10−14 J × 6, 242 ×1018
= 1, 4034" ×105 eV
J
K ≈ 0,14 MeV
(d) A diferença de potencial necessária para que a partícula alfa atinja a energia K é dada pela razão
entre a energia da partícula, representada por K e a sua carga q:
−14
K K ( 2, 2484" ×10 J )
ΔV = =
=
= 70262," V
q 2e
2 (1, 60 ×10−19 C )
ΔV ≈ 70 kV
[Início seção]
[Início documento]
16. Um feixe de elétrons, cuja energia cinética é K, emerge de uma lâmina fina na “janela” da
extremidade do tubo de um acelerador. Existe uma placa de metal, perpendicular à direção do
feixe emergente, a uma distância d desta janela. Veja Fig. 30. (a) Mostre que podemos evitar
que o feixe colida com a placa aplicando um campo magnético B, tal que
B≥
2mK
,
e2 d 2
onde m e e são a massa e a carga do elétron. (b) Qual deve ser o sentido de B?
________________________________________________________________________________________________________
a
Cap. 34 – O Campo Magnético
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
5
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
y
z
x
(Pág. 150)
Solução.
(a) Para seguir a trajetória descrita no esquema acima, o feixe de elétrons deve interagir com um
campo magnético B que tenha a direção +z. A trajetória será circular com raio d e força centrípeta
Fc igual à força magnética FB sobre os elétrons.
Fc = FB
B
mv 2
= evB
d
mv
B=
ed
m2v 2
e2 d 2
A velocidade v dos elétrons pode ser obtida a partir da energia cinética K:
1
K = mv 2
2
2K
v2 =
m
Substituindo-se (2) em (1):
B2 =
(1)
(2)
⎛ 2K ⎞
m2 ⎜
⎟
⎝ m ⎠ = 2mK
B2 =
e2 d 2
e2 d 2
2mK
(3)
ed
Para este valor de campo magnético o feixe de elétrons irá tangenciar a placa metálica. Um valor
maior de B aumentará a força centrípeta que, por sua vez, reduzirá o raio da trajetória circular. Isto
fará com que o feixe se afaste da placa metálica. Portanto, valores maiores de B, dado por (3)
também são soluções para este problema. Logo:
B=
2mK
ed
(b) Vetor campo magnético:
B≥
B=
2mK
k
ed
________________________________________________________________________________________________________
a
Cap. 34 – O Campo Magnético
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
6
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
[Início seção]
[Início documento]
22. A Fig. 32 mostra um dispositivo usado para medir as massas dos íons. Um íon de massa m e
carga +q é produzido basicamente em repouso pela fonte S, a partir de uma descarga através do
gás no interior de uma câmara. O íon é acelerado por uma diferença de potencial V e penetra um
campo magnético B. Ele se move no interior do campo em semicírculo, colidindo com uma
chapa fotográfica a uma distância x da fenda de entrada. Mostre que a massa m do íon é dada
por
m=
B2q 2
x .,
8V
(Pág. 150)
Solução.
O movimento do íon no interior da câmara é circular, sendo que a força centrípeta Fc é a força
magnética FB:
Fc = FB
B
mv 2 mv 2 2mv 2
=
=
= qvB
x
r
x
2
qB
m=
x
2v
q2 B2 2
x
(1)
4v 2
Agora precisamos determinar a velocidade do íon na câmara. No início do experimento, o íon parte
do repouso e é acelerado pela diferença de potencial V. O íon fica sujeito a um movimento com
aceleração constante, que pode ser descrito por:
m2 =
v 2 = v02 + 2ad
(2)
Na Eq. (2), a velocidade inicial v0 é zero, pois o íon parte do repouso. A aceleração a pode ser
obtida por meio da seguinte operação, onde FE é a força elétrica que age no íon, E é o campo
elétrico na região onde o íon é acelerado e d é a distância que o íon percorre durante o tempo de
aceleração:
________________________________________________________________________________________________________
a
Cap. 34 – O Campo Magnético
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
7
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
V
q
FE qE
qV
a=
=
= d =
m
m
m
md
Substituindo-se (3) em (2):
qV
2qV
v2 = 2
d=
md
m
Substituindo-se (4) em (1):
m2 =
(3)
(4)
q2 B2 2
x
2qV
4
m
qB 2 2
m=
x
8V
[Início seção]
[Início documento]
25. Uma partícula neutra está em repouso num campo magnético uniforme de módulo B. No
instante t = 0 ela decai em duas partículas carregadas de massa m cada uma. (a) Se a carga de
uma das partículas é +q, qual a carga da outra? (b) As duas partículas saem em trajetórias
distintas situadas num plano perpendicular a B. Momentos depois as partículas colidem.
Expresse o tempo, desde o decaimento até a colisão, em função de m, B e q.
(Pág. 151)
Solução.
[Início seção]
[Início documento]
26. Um dêuteron se desloca no campo magnético de um cíclotron percorrendo uma órbita de 50 cm
de raio. Devido à leve colisão com um alvo, o dêuteron se divide em um próton e u nêutron,
com uma perda de energia cinética desprezível. Discuta os movimentos subseqüentes de cada
partícula. Suponha que, na quebra, a energia do dêuteron seja igualmente dividida pelo próton e
pelo nêutron.
(Pág. 151)
Solução.
[Início seção]
[Início documento]
27. (a) Qual a velocidade escalar que um próton necessitaria para circular a Terra na altura do
equador, se o campo magnético da Terra é sempre horizontal e perpendicular ao equador
naquela região? Devem ser considerados os efeitos relativísticos. Admita que o módulo do
campo magnético da Terra, na altura do equador é 41 μT. (b) Represente os vetores velocidade
e campo magnético que correspondem a essa situação.
(Pág. 151)
Solução.
[Início seção]
[Início documento]
________________________________________________________________________________________________________
a
Cap. 34 – O Campo Magnético
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
8
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
33. Calcule a distância total percorrida por um dêuteron, num cíclotron, durante o processo de
aceleração. Suponha que o potencial entre os dês é de 80 kV, o raio dos dês, 53 cm, e a
freqüência do oscilador, 12 MHz.
(Pág. 151)
Solução.
Nossa abordagem consiste em somar o comprimento de cada uma das trajetórias percorridas pelo
dêuteron no ciclotron. Considere o seguinte esquema:
v4
r3
v2
r4
s4
r2
s2
r1 s1
v0
s3
v1
v3
d
A trajetória total (S) do dêuteron consiste na soma de N trajetórias parciais si (s1, s2, ..., sN), que
correspondem cada uma delas a meias circunferências, cada qual com raio ri (r1, r2, ..., rN). Logo:
N
N
N
i =1
i =1
i =1
S = ∑ si = ∑ π ri = π ∑ ri
(1)
O raio de cada trajetória pode ser obtido pela análise da freqüência natural f de rotação da carga no
interior do cíclotron, em que T é o período (constante) de rotação:
1
v
f = =
T 2π r
v
r=
2π f
O valor de cada raio ri (r1, r2, ..., rN) depende do valor correspondente de cada velocidade vi (v1, v2,
..., vN). Logo:
v
ri = i
(2)
2π f
Substituindo-se (2) em (1):
N
v
1
S =π∑ i =
2f
i =1 2π f
N
∑v
i =1
i
(3)
Agora só falta determinar vi e N para completar o cálculo. Supondo que o dêuteron parte do repouso
(v0 = 0) a partir do centro do cíclotron, a velocidade v1 será dada por:
v12 = v02 + 2ad
(4)
Nesta equação, a é a aceleração sofrida pelo dêuteron a cada passagem pela zona central do
cíclotron, onde o campo elétrico atua sobre ele, e d é a distância de separação dos dês. A aceleração
pode ser obtida a partir da força elétrica, por aplicação da segunda lei de Newton:
________________________________________________________________________________________________________
a
Cap. 34 – O Campo Magnético
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
9
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
FE = ma
qE = q
V
= ma
d
qV
md
Substituindo-se (5) em (4):
a=
v1 = v02 +
(5)
2qV
m
O valor de v1 é:
v1 = 0 +
2qV
=
m
2 (1, 60 × 10−19 C )( 80 ×103 V )
( 3,34 ×10
−27
kg )
= 2, 76851" × 106 m/s
De forma geral, teremos:
2qV
m
Vamos analisar uma pequena série de valores de v:
vi = vi2−1 +
v2 = v12 +
2qV
2qV 2qV
4qV
2qV
=
+
=
= 2
= v1 2
m
m
m
m
m
2qV
4qV 2qV
6qV
2qV
=
+
=
= 3
= v1 3
m
m
m
m
m
E assim por diante. Logo:
v3 = v22 +
vi = v1 i
(5)
A maior velocidade que o dêuteron poderá atingir será vN, o que corresponderá a um raio rN, que é
conhecido, pois é o próprio raio do cíclotron. Podemos aplicar este raciocínio combinando as Eqs.
(2) e (5):
rN =
vN
v N
= 1
2π f
2π f
2
6
4π 2 f 2 rN2 4π (12 ×10 Hz ) ( 0,53 m )
N=
=
= 208,34" meias-voltas
2
v12
( 2, 76851"×106 m/s )
2
2
N ≈ 208 meias-voltas
Finalmente podemos calcular a trajetória total substituindo (5) em (3):
1
S=
2f
N
v
v1 i = 1
∑
2f
i =1
( 2, 76851"×10 m/s )
∑ i = 2 (12 ×10 Hz ) ( 2006,89") = 231,504" m
6
208
6
i =1
S ≈ 230 m
[Início seção]
[Início documento]
38. Mostre que a razão entre o campo elétrico Hall E e o campo elétrico Ec, responsável pela
corrente, é
________________________________________________________________________________________________________
a
Cap. 34 – O Campo Magnético
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
10
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
E
B
,
=
Ec neρ
onde ρ é a resistividade do material. (b) Calcule numericamente a razão, no Exemplo 3. Veja
Tabela 1, no Cap. 32.
(Pág. 152)
+
+
+
+
+
+
+
+
E
+
+
+
+
+
+
+
FB
+
−
FE
+
Ec
vd
+
+
+
+
+
+
+
+
+
+
+
+
+
Solução.
Considere o seguinte esquema:
i
+
+
+
+
+
+
+
+
+
+
B
Quando uma corrente elétrica i trafega por uma chapa metálica sujeita a um campo magnético B
ortogonal à chapa, uma força magnética FB atua sobre os elétrons, forçando-os para uma das laterais
da chapa (direita, no esquema acima), sendo que o lado oposto fica carregado positivamente. A
separação das cargas gera um campo elétrico (campo elétrico Hall, E) que também age sobre os
elétrons, por meio de uma força elétrica FE, forçando-os no sentido oposto ao da força magnética.
No equilíbrio eletromagnético, teremos:
FE = FB
B
eE = evd B
E = vd B
(1)
Na expressão acima, e é carga dos elétrons e vd é a velocidade de deriva dos elétrons na chapa
metálica, que está relacionada com a densidade de corrente J por meio da seguinte expressão:
E
J = nevd = c
ρ
Na expressão acima, Ec é o campo elétrico que age na direção da corrente elétrica, sendo este
campo o responsável pela corrente, n é o número de portadores de carga por unidade de volume e ρ
é a densidade de corrente. Resolvendo-se para Ec:
Ec = neρ vd
(2)
Dividindo-se (1) por (2):
E
B
=
Ec neρ
[Início seção]
[Início documento]
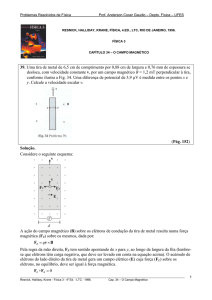
39. Uma tira de metal de 6,5 cm de comprimento por 0,88 cm de largura e 0,76 mm de espessura se
desloca, com velocidade constante v, por um campo magnético B = 1,2 mT perpendicular à tira,
conforme ilustra a Fig. 34. Uma diferença de potencial de 3,9 μV é medida entre os pontos x e
________________________________________________________________________________________________________
a
Cap. 34 – O Campo Magnético
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
11
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
y. Calcule a velocidade escalar v.
(Pág. 152)
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
Solução.
Considere o seguinte esquema:
v
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
E
+
+
FB
+
−
FE
+
+
+
+
v
V
d
A ação do campo magnético (B) sobre os elétrons de condução da tira de metal resulta numa força
magnética (FB) sobre os mesmos, dada por:
FB = qv × B
B
Pela regra da mão direita, FB tem sentido apontando de x para y, ao longo da largura da fita (lembrese que elétrons têm carga negativa, que deve ser levado em conta na equação acima). O acúmulo de
elétrons do lado direito da tira de metal gera um campo elétrico (E) cuja força (FE) sobre os
elétrons, no equilíbrio, deve ser igual à força magnética.
FE +FB = 0
B
qE + qv × B = 0
E = −v × B
O módulo do campo elétrico, que é a razão entre a diferença de potencial V entre as laterais da tira
de largura d, é dado por:
V
E = = vB
d
Logo:
V
v=
Bd
________________________________________________________________________________________________________
a
Cap. 34 – O Campo Magnético
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
12
Problemas Resolvidos de Física
v=
Prof. Anderson Coser Gaudio – Depto. Física – UFES
3,9×10-6 V
= 0,3693" m / s
(1,2×10-3T).(8,8×10-3m)
v ≈ 37 cm/s
[Início seção]
[Início documento]
41. Um fio rígido de 62,0 cm de comprimento e 13,0 g de massa está suspenso por um par de fios
flexíveis, num campo magnético de 440 mT. Determine a intensidade e o sentido da corrente no
fio rígido, necessários para anular a tensão nos fios flexíveis de suporte. Veja Fig. 35.
(Pág. 152)
Solução.
[Início seção]
[Início documento]
42. Um fio de metal de massa m desliza, sem atrito, sobre dois trilhos horizontais separados por
uma distância d, conforme vemos na Fig. 36. Os trilhos estão num campo magnético uniforme
vertical B. Uma corrente constante i, fornecida por um gerador G, passa de um trilho para o
outro através do fio de metal, retornando ao gerador. Determine a velocidade (módulo e sentido)
do fio em função do tempo, supondo que em t = 0 ele está em repouso.
z
y
x
(Pág. 152)
Solução.
Considere o esquema abaixo:
B
z
F
d
y
x
A velocidade do fio em função do tempo é dada por:
v = v 0 + at
i
(1)
Para o cálculo da aceleração a, primeiro precisamos da força magnética F que age sobre o fio:
________________________________________________________________________________________________________
a
Cap. 34 – O Campo Magnético
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
13
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
F = il × B
F = i ( di ) × ( Bk )
F = −idBj
Agora a aceleração pode ser obtida por meio da segunda lei de Newton:
F −idB
a= =
j
m
m
Lembrando que o fio parte do repouso, v0 = 0, e substituindo-se (2) em (1):
⎛ −idB ⎞
v = 0+⎜
j⎟ t
⎝ m ⎠
(2)
idBt
j
m
Obs.: Neste cálculo foi desprezada a fem induzida devido à variação do fluxo do campo magnético
através do circuito, que é provocada pelo movimento do fio. A fem induzida tem sinal contrário à
fem do gerador, o que provoca a atenuação da corrente no circuito. O resultado disso é a diminuição
da intensidade da força sobre o fio, com as conseqüentes alterações na aceleração e na velocidade
do fio.
v=−
[Início seção]
[Início documento]
43. Considere o projeto de um novo trem elétrico. A máquina seria impulsionada pela força da
componente vertical do campo magnético da Terra sobre um eixo do condutor. a corrente
passaria de um trilho para o outro através das rodas e do eixo condutor, retornando à fonte. (a)
Qual a corrente necessária para fornecer a modesta força de 10 kN? Considere que a
componente vertical do campo magnético da Terra é 10 μT e o comprimento do eixo é de 3,0
m. (b) Qual a potência dissipada em cada ohm de resistência dos trilhos? (c) Esse projeto é
totalmente absurdo ou está nos limites de realização?
(Pág. 152)
Solução.
[Início seção]
[Início documento]
44. A Fig. 37 mostra um fio de uma forma qualquer, que conduz uma corrente i entre os pontos a e
b. O plano do fio é ortogonal a um campo magnético uniforme B. Prove que a força sobre o fio
é a mesma, caso a corrente i fluísse entre a e b por um fio reto. (Sugestão: Substitua o fio por
uma série de “degraus” paralelos e perpendiculares, à linha reta que une a e b.)
(Pág. 152)
________________________________________________________________________________________________________
a
Cap. 34 – O Campo Magnético
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
14
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
Solução.
[Início seção]
[Início documento]
46. Um bastão de cobre de 1,15 kg repousa sobre dois trilhos horizontais, separados de 95,0 cm, e
conduz uma corrente de 53,2 A de um trilho para o outro. O coeficiente de atrito estático é 0,58.
Determine o menor campo magnético (não necessariamente vertical) que seria capaz de fazer o
bastão deslizar.
(Pág. 152)
Solução.
Considere o esquema abaixo:
z
i
N
Fa
i
Fm
P
y
x
i
l
Para que a barra horizontal deslize, a força magnética deve ser maior do que a força de atrito
estático máxima. No limiar do movimento, teremos:
Fa + Fm = 0
A força de atrito estático sobre o bastão é descrita pela seguinte equação, onde μe é o coeficiente de
atrito estático, m é a massa do bastão de cobre e g a aceleração da gravidade:
Fa = − μe mgj
Logo:
Fm = −Fa = μe mgj
A força magnética sobre a barra é dada por:
F = il × B ,
onde
l = li .
Na equação acima, l é o comprimento da barra de cobre. Extraindo-se B de (2):
il × Fm
B=−
2
il
(1)
(2)
(3)
(4)
Substituindo-se (1) e (3) em (4)
B=−
( ili ) × ( μe mgj)
2
( il )
B=−
il μ e mg
B=−
μ e mg
( il )
2
k
k
il
B = 0,12946" T
B ≈ 0,13 T
________________________________________________________________________________________________________
a
Cap. 34 – O Campo Magnético
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
15
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
[Início seção]
[Início documento]
47. Um condutor rígido, comprido, está na direção do eixo x e transporta uma corrente de 5,0 A, no
sentido negativo de x. Um campo magnético B = 3i + 8x2j, com x em metros e B em mT, é
estabelecido. Calcule a força num segmento de 2,0 m do condutor, entre os pontos x = 1,2 m e x
= 3,2 m.
(Pág. 153)
Solução.
[Início seção]
[Início documento]
49. Uma bobina de uma única espira forma um triângulo retângulo de lados iguais a 50 cm, 120 cm
e 130 cm e conduz uma corrente de 4,00 A. A espira está num campo magnético uniforme de
75,0 mT que tem sentido idêntico ao da corrente na hipotenusa da espira. (a) Determine a força
magnética em cada um dos três lados da espira. (b) Mostre que a força magnética total sobre a
espira é nula.
(Pág. 153)
Solução.
[Início seção]
[Início documento]
50. O raio da face de um relógio de parede circular tem 15 cm. Em volta dessa face são enroladas
seis voltas de fio, que conduz uma corrente de 2,0 A no sentido horário. O relógio está dentro de
um campo magnético uniforme, constante, de 70 mT (mas continua funcionando perfeitamente).
Exatamente às 13:00 h, o ponteiro das horas aponta no sentido do campo magnético externo. (a)
Depois de quantos minutos o ponteiro dos minutos apontará no sentido do torque provocado
pelo campo magnético sobre o enrolamento? (b) Qual o módulo desse torque?
(Pág. 153)
Solução.
(a) Considere o esquema abaixo:
12 1
B
y
x
μ
R
3
+
z
θ 2
i
O torque do campo magnético sobre o enrolamento é dado por:
τ = μ×B
(1)
O enunciado do problema nos revela que o vetor campo magnético B aponta para o marcador “1”
do relógio e, portanto, faz um ângulo de θ = 60o com a horizontal. Vetor campo magnético:
B = B cos θ i + B sen θ j
O momento magnético das espiras μ (direção e sentido segundo a regra da mão direita) é função no
número de espiras N, da corrente i e da área do enrolamento A:
μ = − NiAk
Substituindo-se as expressões de μ e B em (1):
________________________________________________________________________________________________________
a
Cap. 34 – O Campo Magnético
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
16
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
τ = ( − NiAk ) × ( B cosθ i + B sen θ j)
τ = NiAB ( sen θ i − cosθ j)
Considerando-se que θ = 60o, percebe-se que τ aponta para a marca “4” do relógio (veja esquema
abaixo). Logo, serão necessários 20 min para que o ponteiro dos minutos atinja esta direção.
12 1
2
3
τ
4
(b) O módulo do torque vale:
τ=
( NiAB sen θ ) + ( NiAB cosθ )
2
2
= NiAB
( sen θ ) + ( cosθ )
2
2
= Ni (π r 2 ) B 1
τ = Nπ ir 2 B = 6π ( 2, 0 A )( 0,15 m ) ( 70 ×10−3 T ) = 0, 05937" N.m
2
τ ≈ 0, 059 N.m
[Início seção]
[Início documento]
51. Um fio de comprimento L conduz uma corrente i. Mostre que se o fio forma uma bobina
circular, o torque máximo desenvolvido por um determinado campo magnético acontece quando
a bobina tem apenas uma espira e seu módulo é dado por
τ=
1 2
L iB .
4π
(Pág. 153)
Solução.
Como o comprimento do fio é fixo, quanto maior o número de espiras menor será a área de cada
uma. O comprimento do fio (L) deve ser igual ao número de voltas (N) vezes o comprimento de
cada volta (2πr).
L = 2π rN
L
(1)
r=
2π N
O torque da força magnética sobre a espira vale:
τ = μ×B
τ = NiABsenθ
τ = Ni (π r 2 ) Bsenθ
Naturalmente o ângulo θ deverá ser igual a π/2 para maximizar o torque:
τ = π Nir 2 B
Substituindo-se (1) em (2):
(2)
2
⎛ L ⎞
⎟ B
⎝ 2π N ⎠
τ = π Ni ⎜
________________________________________________________________________________________________________
a
Cap. 34 – O Campo Magnético
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
17
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
iL2 B
4π N
Como τ ∝ 1/N, conclui-se que para maximizar o torque o número de espiras deverá ser o menor
possível, ou seja, igual a 1 (N = 1).
τ=
τ=
iL2 B
4π
[Início seção]
[Início documento]
53. A Fig. 40 mostra um fio em anel de raio a, perpendicular à direção de um campo magnético
divergente, radialmente simétrico. O campo magnético tem a mesma intensidade B em todos os
pontos do anel, e seu sentido faz um ângulo θ com a normal ao plano do anel em todos os
pontos. A ponta torcida do fio não têm nenhum efeito sobre o problema. Se o anel conduz uma
corrente i, determine o módulo e o sentido da força que o campo exerce sobre ele, conforme
mostrado na figura.
(Pág. 153)
Solução.
Considere o seguinte esquema, que mostra a vista lateral do sistema:
z
dF θ B
x
y
dl
O elemento de força magnética dF que age no anel pode ser decomposta em três componentes, dFx,
dFy e dFz:
dF = dFx i + dFy j + dFz k
A força total F é obtida por integração ao longo da circunferência do anel:
F = ∫ dFx i + ∫ dFy j + ∫ dFz k
As duas primeiras integrais são nulas devido à simetria envolvida no problema. Logo:
F = ∫ dFsenθ k
(1)
O elemento de força dF sobre um elemento de fio dl vale:
dF = idl × B
dF = idlB
Substituindo-se (2) em (1):
F = ∫ idlBsenθ k = iBsenθ
(2)
( ∫ dl ) k
2π a
0
F = 2π aiBsenθ k
________________________________________________________________________________________________________
a
Cap. 34 – O Campo Magnético
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
18
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
[Início seção]
[Início documento]
55. A Fig. 41 mostra um cilindro de madeira com massa m = 262 g e comprimento L = 12,7 cm,
com um fio enrolado longitudinalmente em volta dele, de maneira que o plano do enrolamento,
com N = 13 voltas, contém o eixo do cilindro e é paralelo a um plano que tem uma inclinação θ
com a horizontal. O cilindro está sobre esse plano inclinado, e o conjunto está sendo submetido
a um campo magnético uniforme, vertical, de 477 mT. Qual a menor corrente que deve circular
no enrolamento, de forma a evitar que o cilindro role para baixo?
(Pág. 153)
Solução.
Considere o seguinte esquema, que mostra as forças externas que agem sobre o cilindro:
−Fm
y
z
Fa
P
x
Fm
N
No esquema, foram omitidas as duas forças magnéticas em z, que agem sobre os lados das espiras
paralelos à pagina. Para que o cilindro não role rampa abaixo ou acima, o torque resultante em
relação ao centro de massa, ou em relação ao ponto de contato do cilindro com a rampa, deve ser
zero. Em relação ao centro de massa do cilindro agem apenas os torques devido à força magnética
τm e à força de atrito estático τa. Logo:
τm + τa = 0
(1)
Note que nem a força peso nem a normal exercem torques em relação ao centro de massa. O torque
da força magnética em relação ao eixo do cilindro em z vale:
τ m = μ × B = NiABsenθ k
(2)
O torque da força de atrito em relação ao mesmo eixo é dado por:
τ a = ra × Fa
(3)
O cálculo da força de atrito pode ser feito pelas componentes das forças em x e y. Forças em x:
N x − Fax = 0
________________________________________________________________________________________________________
a
Cap. 34 – O Campo Magnético
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
19
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
Nsenθ − Fa cosθ = 0
N=
Fa cos θ
senθ
(4)
Forças em y:
N y + Fay − P = 0
Ncosθ + Fa senθ = mg
(5)
Substituindo-se (4) em (5):
Fa cos θ
cosθ + Fa senθ = mg
senθ
⎛ cos 2 θ + sen 2θ ⎞
Fa ⎜
⎟ = mg
senθ
⎝
⎠
Fa = mgsenθ
(6)
Pode-se agora resolver (3):
τ a = −rmgsenθ k
(7)
Substituindo-se (2) e (7) em (1):
NiAB sen θ k − rmg sen θ k = 0
Ni (2rL ) B = rmg
2NiLB = mg
( 0, 262 kg ) ( 9,81 m/s 2 )
mg
i=
=
= 1, 6318" A
2 NLB 2 (13)( 0,127 m )( 0, 477 T )
i ≈ 1, 63 A
[Início seção]
[Início documento]
________________________________________________________________________________________________________
a
Cap. 34 – O Campo Magnético
Resnick, Halliday, Krane - Física 3 - 4 Ed. - LTC - 1996.
20
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
RESNICK, HALLIDAY, KRANE, FÍSICA, 5.ED., LTC, RIO DE JANEIRO, 2003.
FÍSICA 3
CAPÍTULO 32 - O CAMPO MAGNÉTICO
EXERCÍCIOS
01
11
21
31
41
02
12
22
32
42
03
13
23
33
43
04
14
24
34
44
05
15
25
35
45
06
16
26
36
46
07
17
27
37
47
08
18
28
38
48
09
19
29
39
49
10
20
30
40
50
07
17
27
37
47
08
18
28
38
48
09
19
29
39
49
10
20
30
40
50
PROBLEMAS
01
11
21
31
41
02
12
22
32
42
03
13
23
33
43
04
14
24
34
44
05
15
25
35
45
06
16
26
36
46
[Início documento]
[Início seção]
[Início documento]
________________________________________________________________________________________________________
a
Cap. 32 – O Campo Magnético
Resnick, Halliday, Krane - Física 3 - 5 Ed. - LTC - 2003.
21