Matemática - Setor A Aulas 13 e 14 Aulas 15 e 16

Matemática - Setor A
Aulas 13 e 14
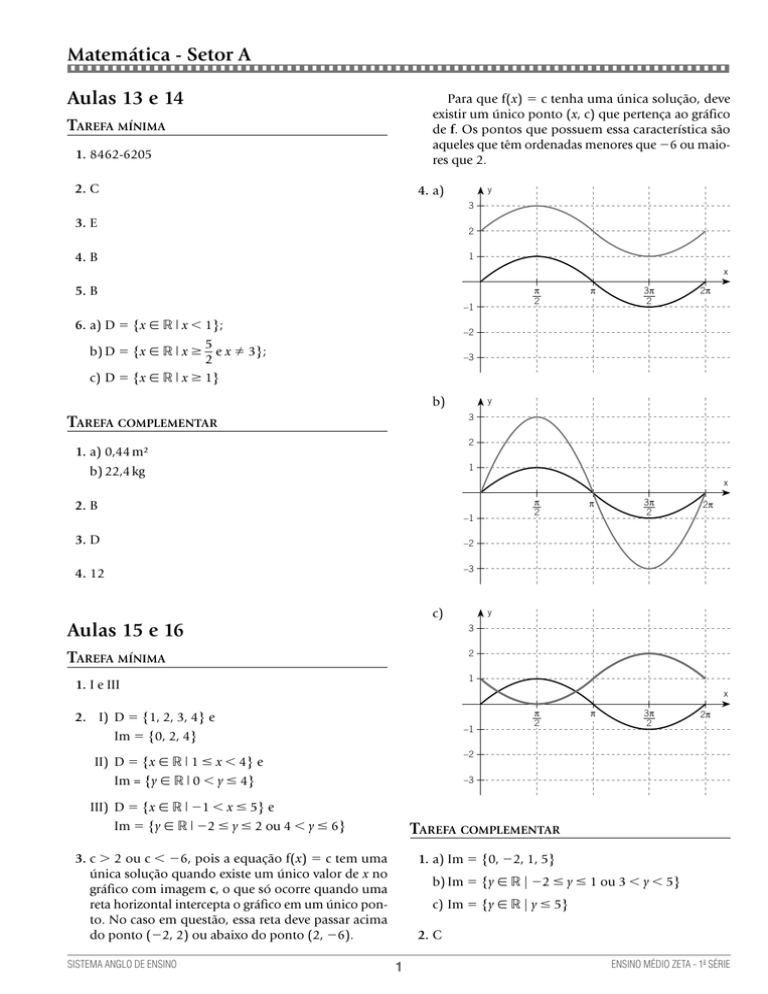
Para que f(x) = c tenha uma única solução, deve
existir um único ponto (x, c) que pertença ao gráfico
de f. Os pontos que possuem essa característica são
aqueles que têm ordenadas menores que −6 ou maiores que 2.
TAREFA MÍNIMA
1. 8462-6205
2. C
4. a)
y
3
3. E
2
4. B
1
x
π
2
5. B
–1
6. a) D = {x ∈ ℝ | x < 1};
5
b) D = {x ∈ ℝ | x ≥ e x ≠ 3};
2
c) D = {x ∈ ℝ | x ≥ 1}
π
3π
2
2π
–2
–3
b)
y
3
TAREFA COMPLEMENTAR
2
1. a) 0,44 m²
1
b) 22,4 kg
x
π
2
2. B
–1
3. D
3π
2
2π
–2
–3
4. 12
c)
y
Aulas 15 e 16
3
TAREFA MÍNIMA
2
1
1. I e III
x
2. I) D = {1, 2, 3, 4} e
Im = {0, 2, 4}
–1
π
2
π
3π
2
2π
–2
II) D = {x ∈ ℝ | 1 ≤ x < 4} e
Im = {y ∈ ℝ | 0 < y ≤ 4}
–3
III) D = {x ∈ ℝ | −1 < x ≤ 5} e
Im = {y ∈ ℝ | −2 ≤ y ≤ 2 ou 4 < y ≤ 6}
TAREFA COMPLEMENTAR
3. c > 2 ou c < −6, pois a equação f(x) = c tem uma
única solução quando existe um único valor de x no
gráfico com imagem c, o que só ocorre quando uma
reta horizontal intercepta o gráfico em um único ponto. No caso em questão, essa reta deve passar acima
do ponto (−2, 2) ou abaixo do ponto (2, −6).
SISTEMA ANGLO DE ENSINO
π
1. a) Im = {0, −2, 1, 5}
b) Im = {y ∈ ℝ | −2 ≤ y ≤ 1 ou 3 < y < 5}
c) Im = {y ∈ ℝ | y ≤ 5}
2. C
1
ENSINO MÉDIO ZETA - 1a SÉRIE
3. a)
2000
b)
Salário
y
3
1500
x
1000
–3
0
D = ℝ e Im = ℝ
500
Venda
0
0
500
1000
1500
2000
c)
b)
2000
y
Salário
3
1500
x
0
1000
1,5
D = ℝ e Im = ℝ
500
Venda
0
0
500
1000
1500
d)
2000
y
2
4.
y
x
0
24
2
–1
16
D = ℝ e Im = {x ∈ ℝ | x = −1 ou x ≥ 2}
8
x
0
6
12
2. a) R$ 9,10
18
Im = {8, 16, 24}
b) 10 km
Para pintar qualquer área de x metros quadrados,
com 0 < x ≤ 6, será necessário comprar uma lata, ou
seja, o custo será de 8 reais; analogamente, para pintar qualquer área de x metros quadrados, com
6 < x ≤ 12, serão necessárias duas latas, ao custo de
16 reais; portanto, para pintar qualquer área de x metros quadrados, com 12 < x ≤ 18, serão necessárias
três latas, que custarão 24 reais.
c) f(x) = 0,70x + 3,50, com x ≥ 0
d)
y
10,50
3,50
x
0
10
9
3. y = x + 32
5
Aulas 17 e 18
TAREFA MÍNIMA
1. a)
4. a) Plano 1: y = 1,2x
Plano 2: y = 0,4x + 40
y
2
b) Plano 1: R$ 1,20 por minuto
Plano 2: R$ 0,40 por minuto
x
0
c) O plano 1.
D = ℝ e Im = {2}
SISTEMA ANGLO DE ENSINO
d) Para 50 minutos, R$ 60,00.
2
ENSINO MÉDIO ZETA - 1a SÉRIE
TAREFA COMPLEMENTAR
1. a)
2. f(x) =
2,50x
se 0 ≤ x ≤ 10
1,50x + 10 se x > 10.
y
1
y
40
25
x
1
2
0
1
D = [0, 1] e Im = [0, 1]
x
b)
y
0
20
10
1
3. A
x
0
1
2
1
4. a) f(x) =
2
c) Para x = 0 ou x = . Os valores de x para os quais
3
f(x) = g(x) são as abscissas dos pontos comuns aos
−x + 21 se 0 ≤ x ≤ 10
−x + 31 se 10 < x ≤ 20
−x + 41 se 20 < x ≤ 30
b) Nos dias 6, 16 e 26.
c) Durante 12 dias.
gráficos de f e g.
Matemática - Setor B
Aulas 13 e 14
3. 45°
TAREFA MÍNIMA
4. A
1. a) 270°
b) 220°
c) 225°
d) 50°
2. a) 75°
b) 72°
c) 105°
5. a) 60°
b) 90°
c) Como o ângulo PQ̂R é reto, o arco PSR mede 180°.
Assim, PR é diâmetro da circunferência, ou seja,
passa pelo seu centro.
3. 54°
Aulas 15 e 16
4. 144°
TAREFA MÍNIMA
1. B
5. 70°
2. Não, os dois hexágonos não são semelhantes. Apesar
de terem os ângulos correspondentes com medidas
iguais, os lados correspondentes não são proporcionais. Basta notar que o lado CO tem a mesma medida
nos dois hexágonos, mas os lados BE e MI têm medidas diferentes.
TAREFA COMPLEMENTAR
1. D
2. a) 30°
b) 30° (o triângulo OAT é isósceles, com OT = OA)
c) 120°
d) 120°, pois a medida do ângulo central é igual à
medida do arco correspondente.
SISTEMA ANGLO DE ENSINO
3. a) aproximadamente 382 milhas.
b) y ≈ 1,6
4. D
3
ENSINO MÉDIO ZETA - 1a SÉRIE
TAREFA COMPLEMENTAR
8
2. a) cm
3
1. 162 m2
b)
24
cm
5
3. 12 m
2. Sim. Sejam L e as medidas de um lado dos pentágonos regulares ABCDE e FGHIJ, respectivamente. Então, temos:
• os lados correspondentes têm medidas proporcionais, pois a razão entre eles é sempre L/ ;
• os ângulos correspondentes têm medidas iguais,
pois todos eles medem 108º.
Assim, os dois pentágonos são semelhantes.
4. 60 m
TAREFA COMPLEMENTAR
1. A
2. 4 cm
3. D
3. a) 0,0023 mm
b) 0,0075 mm
c) 3,3
4. a) Como  = Q̂ = 90° e Ĉ = Ĉ = α, os triângulos ABC
e QDC têm dois pares de ângulos correspondentes
com medidas iguais. Logo, ∆ABC ∼ ∆QDC.
Analogamente, Q̂ = Ê = 90° e D̂ = D̂ (são os
ângulos de incidência e reflexão).
Assim, ∆QDC ∼ ∆EDV.
6
b) m
17
4. √3 cm
Aulas 17 e 18
TAREFA MÍNIMA
1. a) 45°
b) 25°
c) RPQ
SISTEMA ANGLO DE ENSINO
d) ABC
e) PR
5. D
6. 696.537 km
4
ENSINO MÉDIO ZETA - 1a SÉRIE